Spark GraphX学习（一）图（GraphX ）简介

SparkGraphX快速入门

1、图（GraphX）

1.1、基本概念

图是由顶点集合(vertex)及顶点间的关系集合（边edge）组成的一种数据结构。

这里的图并非指代数中的图。图可以对事物以及事物之间的关系建模，图可以用来表示自然发生的连接数据，如：社交网络、互联网web页面

常用的应用有：在地图应用中找到最短路径、基于与他人的相似度图，推荐产品、服务、人际关系或媒体。

2、术语

2.1、顶点和边

一般关系图中，事物为顶点，关系为边

2.2、有向图和无向图

在有向图中，一条边的两个顶点一般扮演者不同的角色，比如父子关系、页面A连接向页面B；

在一个无向图中，边没有方向，即关系都是对等的，比如qq中的好友。

GraphX中有一个重要概念，所有的边都有一个方向，那么图就是有向图，如果忽略边的方向，就是无向图。

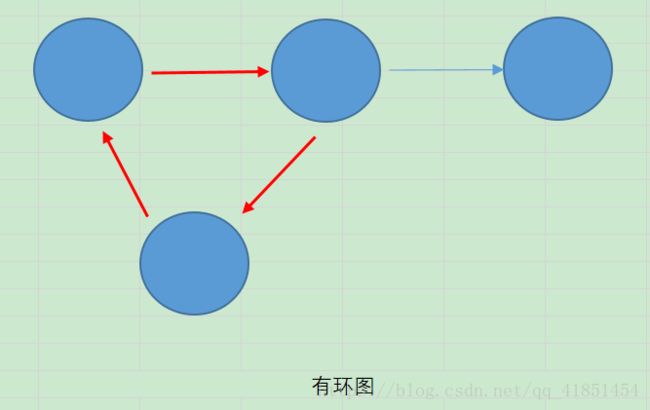
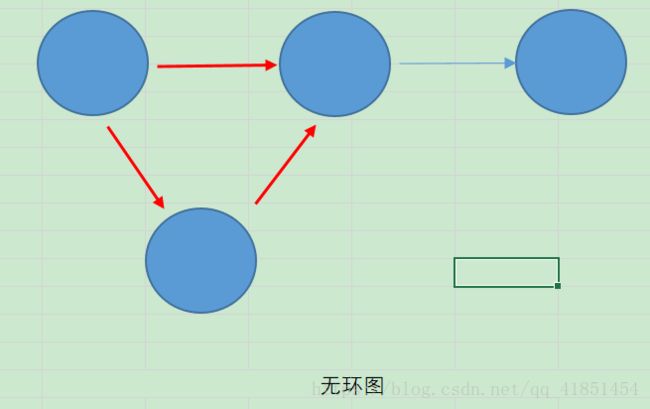
2.3、有环图和无环图

有环图是包含循环的，一系列顶点连接成一个环。无环图没有环。在有环图中，如果不关心终止条件，算法可能永远在环上执行，无法退出。

2.4、度、出边、入边、出度、入度

度表示一个顶点的所有边的数量

出边是指从当前顶点指向其他顶点的边

入边表示其他顶点指向当前顶点的边

出度是一个顶点出边的数量

入度是一个顶点入边的数量

2.5、超步

图进行迭代计算时，每一轮的迭代叫做一个超步

3、图处理技术

图处理技术包括图数据库、图数据查询、图数据分析和图数据可视化。

3.1、图数据库

Neo4j、Titan、OrientDB、DEX和InfiniteGraph等基于遍历算法的、实时的图数据库；

3.2、图数据查询

对图数据库中的内容进行查询

3.3、图数据分析

Google Pregel、Spark GraphX、GraphLab等图计算软件。传统的数据分析方法侧重于事物本身，即实体，例如银行交易、资产注册等等。而图数据不仅关注事物，还关注事物之间的联系。例如，如果在通话记录中发现张三曾打电话给李四，就可以将张三和李四关联起来，这种关联关系提供了与两者相关的有价值的信息，这样的信息是不可能仅从两者单纯的个体数据中获取的。

3.4、图数据可视化

OLTP风格的图数据库或者OLAP风格的图数据分析系统（或称为图计算软件），都可以应用图数据库可视化技术。需要注意的是，图可视化与关系数据可视化之间有很大的差异，关系数据可视化的目标是对数据取得直观的了解，而图数据可视化的目标在于对数据或算法进行调试。

操作实例：（Scala编写）

import org.apache.log4j.{Level, Logger}  
import org.apache.spark.{SparkContext, SparkConf}  
import org.apache.spark.graphx._  
import org.apache.spark.rdd.RDD  
  
object Test {  
  def main(args: Array[String]) {  
    //屏蔽日志  
    Logger.getLogger("org.apache.spark").setLevel(Level.WARN)  
    //设置运行环境  
    val conf = new SparkConf().setAppName("GraphXTest").setMaster("local[*]")  
    val sc = new SparkContext(conf)  
    //设置顶点和边，注意顶点和边都是用元组定义的 Array  
    //顶点的数据类型是 VD:(String,Int)  
    val vertexArray = Array(  
      (1L, ("Alice", 28)),  
      (2L, ("Bob", 27)),  
      (3L, ("Charlie", 65)),  
      (4L, ("David", 42)),  
      (5L, ("Ed", 55)),  
      (6L, ("Fran", 50))  
    )  
    //边的数据类型 ED:Int  
    val edgeArray = Array(  
      Edge(2L, 1L, 7),  
      Edge(2L, 4L, 2),  
      Edge(3L, 2L, 4),  
      Edge(3L, 6L, 3),  
      Edge(4L, 1L, 1),  
      Edge(5L, 2L, 2),  
      Edge(5L, 3L, 8),  
      Edge(5L, 6L, 3)  
    )  
    //构造 vertexRDD 和 edgeRDD  
    val vertexRDD: RDD[(Long, (String, Int))] = sc.parallelize(vertexArray)  
    val edgeRDD: RDD[Edge[Int]] = sc.parallelize(edgeArray)  
    //构造图 Graph[VD,ED]  
    val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)  
    println("***********************************************")  
    println("属性演示")  
    println("**********************************************************")  
    println("找出图中年龄大于 30 的顶点：")  
    graph.vertices.filter { case (id, (name, age)) => age > 30 }.collect.foreach {  
      case (id, (name, age)) => println(s"$name is $age")  
    }  
    graph.triplets.foreach(t => println(s"triplet:${t.srcId},${t.srcAttr},${t.dstId},${t.dstAttr},${t.attr}"))  
    //边操作：找出图中属性大于 5 的边  
    println("找出图中属性大于 5 的边：")  
    graph.edges.filter(e => e.attr > 5).collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))  
    println  
    //triplets 操作，((srcId, srcAttr), (dstId, dstAttr), attr)  
    println("列出边属性>5 的 tripltes：")  
    for (triplet <- graph.triplets.filter(t => t.attr > 5).collect) {  
      println(s"${triplet.srcAttr._1} likes ${triplet.dstAttr._1}")  
    }  
    println  
    //Degrees 操作  
    println("找出图中最大的出度、入度、度数：")  
  
    def max(a: (VertexId, Int), b: (VertexId, Int)): (VertexId, Int) = {  
      if (a._2 > b._2) a else b  
    }  
  
    println("max of outDegrees:" + graph.outDegrees.reduce(max) + ", max of inDegrees:" + graph.inDegrees.reduce(max) + ", max of Degrees:" +  
      graph.degrees.reduce(max))  
    println  
    println("**********************************************************")  
    println("转换操作")  
    println("**********************************************************")  
    println("顶点的转换操作，顶点 age + 10：")  
    graph.mapVertices { case (id, (name, age)) => (id, (name,  
      age + 10))  
    }.vertices.collect.foreach(v => println(s"${v._2._1} is ${v._2._2}"))  
    println  
    println("边的转换操作，边的属性*2：")  
    graph.mapEdges(e => e.attr * 2).edges.collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))  
    println  
    println("**********************************************************")  
    println("结构操作")  
    println("**********************************************************")  
    println("顶点年纪>30 的子图：")  
    val subGraph = graph.subgraph(vpred = (id, vd) => vd._2 >= 30)  
    println("子图所有顶点：")  
    subGraph.vertices.collect.foreach(v => println(s"${v._2._1} is ${v._2._2}"))  
    println  
    println("子图所有边：")  
    subGraph.edges.collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))  
    println  
    println("**********************************************************")  
    println("连接操作")  
    println("**********************************************************")  
    val inDegrees: VertexRDD[Int] = graph.inDegrees  
    case class User(name: String, age: Int, inDeg: Int, outDeg: Int)  
    //创建一个新图，顶点 VD 的数据类型为 User，并从 graph 做类型转换  
    val initialUserGraph: Graph[User, Int] = graph.mapVertices { case (id, (name, age))  
    => User(name, age, 0, 0)  
    }  
    //initialUserGraph 与 inDegrees、outDegrees（RDD）进行连接，并修改 initialUserGraph中 inDeg 值、outDeg 值  
    val userGraph = initialUserGraph.outerJoinVertices(initialUserGraph.inDegrees) {  
      case (id, u, inDegOpt) => User(u.name, u.age, inDegOpt.getOrElse(0), u.outDeg)  
    }.outerJoinVertices(initialUserGraph.outDegrees) {  
      case (id, u, outDegOpt) => User(u.name, u.age, u.inDeg, outDegOpt.getOrElse(0))  
    }  
    println("连接图的属性：")  
    userGraph.vertices.collect.foreach(v => println(s"${v._2.name} inDeg: ${v._2.inDeg} outDeg: ${v._2.outDeg}"))  
    println  
    println("出度和入读相同的人员：")  
    userGraph.vertices.filter {  
      case (id, u) => u.inDeg == u.outDeg  
    }.collect.foreach {  
      case (id, property) => println(property.name)  
    }  
    println  
    println("**********************************************************")  
    println("聚合操作")  
    println("**********************************************************")  
    println("找出年纪最大的follower：")  
    val oldestFollower: VertexRDD[(String, Int)] = userGraph.aggregateMessages[(String,  
      Int)](  
      // 将源顶点的属性发送给目标顶点，map 过程  
      et => et.sendToDst((et.srcAttr.name,et.srcAttr.age)),  
      // 得到最大follower，reduce 过程  
      (a, b) => if (a._2 > b._2) a else b  
    )  
    userGraph.vertices.leftJoin(oldestFollower) { (id, user, optOldestFollower) =>  
      optOldestFollower match {  
        case None => s"${user.name} does not have any followers."  
        case Some((name, age)) => s"${name} is the oldest follower of ${user.name}."  
      }  
    }.collect.foreach { case (id, str) => println(str) }  
    println  
    println("**********************************************************")  
    println("聚合操作")  
    println("**********************************************************")  
    println("找出距离最远的顶点，Pregel基于对象")  
    val g = Pregel(graph.mapVertices((vid, vd) => (0, vid)), (0, Long.MinValue), activeDirection = EdgeDirection.Out)(  
      (id: VertexId, vd: (Int, Long), a: (Int, Long)) => math.max(vd._1, a._1) match {  
        case vd._1 => vd  
        case a._1 => a  
      },  
      (et: EdgeTriplet[(Int, Long), Int]) => Iterator((et.dstId, (et.srcAttr._1 + 1+et.attr, et.srcAttr._2))) ,  
      (a: (Int, Long), b: (Int, Long)) => math.max(a._1, b._1) match {  
        case a._1 => a  
        case b._1 => b  
      }  
    )  
    g.vertices.foreach(m=>println(s"原顶点${m._2._2}到目标顶点${m._1},最远经过${m._2._1}步"))  
  
    // 面向对象  
    val g2 = graph.mapVertices((vid, vd) => (0, vid)).pregel((0, Long.MinValue), activeDirection = EdgeDirection.Out)(  
      (id: VertexId, vd: (Int, Long), a: (Int, Long)) => math.max(vd._1, a._1) match {  
        case vd._1 => vd  
        case a._1 => a  
      },  
      (et: EdgeTriplet[(Int, Long), Int]) => Iterator((et.dstId, (et.srcAttr._1 + 1, et.srcAttr._2))),  
      (a: (Int, Long), b: (Int, Long)) => math.max(a._1, b._1) match {  
        case a._1 => a  
        case b._1 => b  
      }  
    )  
//    g2.vertices.foreach(m=>println(s"原顶点${m._2._2}到目标顶点${m._1},最远经过${m._2._1}步"))  
    sc.stop()  
  }  
  
}