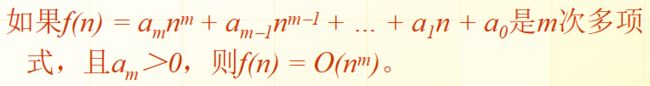【算法设计与分析】算法的时间复杂度（介绍O渐近上界，Ω渐近下界，θ准确的界）

什么是时间复杂度？

我们先看看一些函数的渐近表达式：

关于时间复杂度的基本要点：

1.时间复杂度反映的是随着问题规模的变大，计算所需的时间的增长速度，与系数的多少关系不大

2.算法的渐近时间复杂度，简称时间复杂度，很多时候为了便于理解，直接把时间复杂度等同于O（）是可以的。

3.常见的时间复杂度，及其增长速度比较

O(1)＜O(log n)＜O(n)＜O(nlog n)＜O(n^2)＜O(n^3)< O(2^n)＜O(n!)＜O(n^n)

可以这么说,看到这里就已经基本掌握时间复杂度的概念了，对于分析常见时间复杂度问题是没问题的

当然，若想深入了解这块知识，请参考课本及其他博客，并耐心地看完下面的内容

（阅读时请结合例子理解）

 

一、大O记号(渐近上界记号)

定义1-1  

设函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在两个正常数c和n0，使得当n≥n0时，有f(n)≤cg(n)，则记做f(n) = O(g(n))，称为大O记号（big Oh notation） 称g(n)是f(n)的一个上界 注： f(n)的阶不高于g(n)

 

例1-1   f(n) = 2n + 3 = O(n)

当n≥3时，2n+3≤3n，

所以，可选c = 3，n0 = 3。对于n≥n0，f(n) = 2n + 3≤3n，

所以， f(n) = O(n) 。这意味着，当n≥3时，该程序步不会超过3n。

 

例1-2  f(n) = 10n2 + 4n + 2 = O(n2)

对于n≥2时，有10n2 + 4n + 2≤10n2 + 5n，

并且当n≥5时，5n≤n2， 因此，可选c = 11, n0 = 5；

对于n≥n0，f(n) = 10n2 + 4n + 2≤11n2， 所以f(n) = O(n2)。

 

例1-3 10n2 + 9 ！=O(n)

使用反证法，假定存在c和n0，使得对于n≥n0，10n2 + 9≤cn始终成立，

那么有10n + 9/n≤c，即n≤c/10 - 9/(10n)总成立。

但此不等式不可能总成立，取n = c/10 + 1时，该不等式便不再成立。

 

重要定理

 

渐近时间复杂度    

使用大O记号及下面定义的几种渐近表示法表示的算法时间复杂度，

称为算法的渐近时间复杂度（asymptotic complexity），简称时间复杂度

适当选择关键操作，算法的渐近时间复杂度可以由关键操作的执行次数之和来计算

一般地，关键操作的执行次数与问题的规模有关，是n的函数

 

【程序1-4】  矩阵乘法

for（i=0; i

总的时间： n3+ n2(n+1)+ n2+ n(n+1)+ n+1 =2n3+3n2+2n+1   渐进时间复杂度：O(n3)

 
大O运算规则:

(1) O(f)+O(g)=O(max(f, g))
(2) O(f)+O(g)=O(f+g)
(3) O(f)O(g)=O(fg)
(4) 如果g(N)=O(f(N)), 则O(f)+O(g)=O(f)
(5) O(Cf(N))=O(f(N)), 其中C是一个正常数
(6) f=O(f)

 

二、Ω记号(渐近下界记号)

定义2-2    设有函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在两个正常数 c和n0，使得当n≥n0时，有f(n)≥c g(n)，则记做f(n) = Ω (g(n))，称为Ω记号（omega notation）。 注： f(n)的阶不低于g(n)

（Ω的相关概念实际上就是O（n）颠倒过来）

 

例1-5  f(n) = 2n + 3 =Ω(n)

对所有n，2n+3≥2n，可选c = 2，n0=0。

对于n≥n0，f(n) = 2n+3≥2n，所以，f(n) = Ω(n)，即2n + 3∈Ω(n)。

 

例1-6  f(n) = 10n2 + 4n + 2 = Ω(n2)

对所有n，10n2 + 4n + 2≥10n2，可选c = 10，n0 = 0。

对于n≥n0，f(n) = 10n2 + 4n + 2≥10n2，所以，f(n) =Ω(n^2)。

重要定理

 

 

三、 θ记号（紧渐近界记号）

定义1-3 设有函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在正常数c1，c2和n0，使得当n≥n0时，有c1 g(n)≤f(n)≤c2 g(n)，则记做f(n) = θ(g(n))，称为θ记号（Theta notation）。 注：此时f(n)和g(n)同阶

例1-7  f(n) = 2n + 3 = θ(n)

例1-8  f(n) = 10n2 + 4n + 2 = θ(n^2)

 

四、算法按时间复杂度分类

多项式时间算法

凡渐近时间复杂度有多项式时间限界的算法称做多项式时间算法（polynomial time algorithm）

O(1)＜O(log n)＜O(n)＜O(nlog n)＜O(n^2)＜O(n^3)

指数时间算法

渐近时间复杂度为指数函数限界的算法称做指数时间算法（exponential time algorithm）

O(2^n)＜O(n!)＜O(n^n)

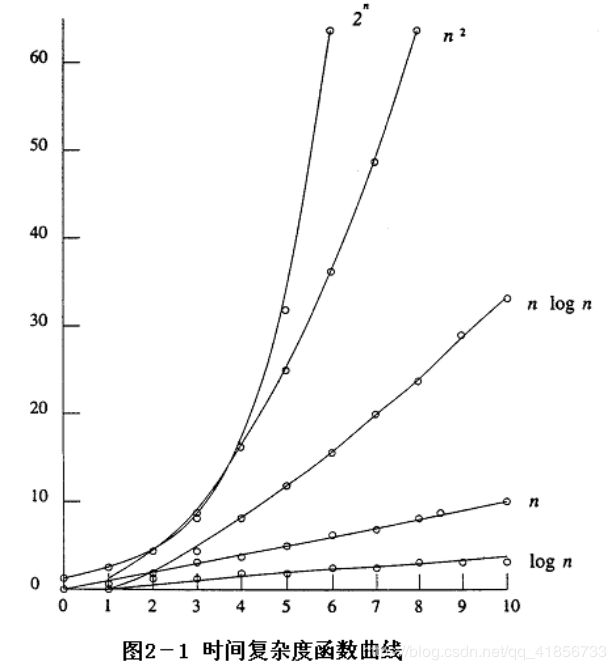
时间复杂度增长示意图

判断时间复杂度是否为准确值相关定理

如果存在正常数n0, 使得当n≥n0时有f(n)>0, g(n)>0

并且    则f(n)=O(g(n))

如果存在正常数n0, 使得当n≥n0时有f(n)>0, g(n)>0

并且   则f(n)=θ(g(n))

书上相关例题参考答案：