LeetCode 198. House Robber 打家劫舍(Java)
题目:
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
Example 2:
Input: [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.
解答:
本题是个经典的动态规划问题。
每个房间,都有偷和不偷两种情况。
假设有[A,B,C,D,…]等房间,则我们自上而下进行分析,如下图所示:
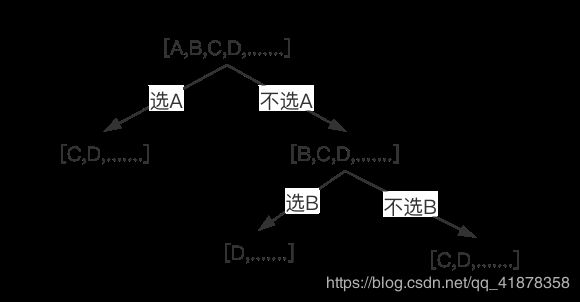
A房间有偷或不偷两种情况,
于是我们可以知道,虽然我们开始想要得到在ABCD中进偷窃的最大收益,但是现在这个问题变成了两个子问题:
- 偷[B,C,D,…]的最大收益
- 偷[C,D,…]的最大收益+房间A的收益
然后,比较以上两个子问题,获取其中的最大值,就能得到在[A,B,C,D,…]中选择房间的最大收益。
以此类推…
针对在BCD中选择房子获得最大收益,可以进行同样的的拆分得到两个子问题:
- 偷[C,D,…]的最大收益
- 偷[D,…]的最大收益+房间B的收益
这时我们发现,计算在[C,D,…]中选择的最大收益这个问题,在计算[A,B,C,D,…]的时候也出现了。我们可以重新计算一遍,也可以把之前的答案保存下来,这样就避免了重复计算。
根据以上分析,我们可以得出递归方程为:
f[n] = max(f[n-1], f[n-2] + nums[n])
因此本问题转化为了一个递归问题,其中:
-
最后状态为:f[n]的值,可以对nums[n]取或者不取
-
转移方程为:f[n] = max( f[n-1], f[n-2] + nums[n]) ,其中n>=2
-
初始条件为:
f[0] = nums[0],
f[1] = max(nums[0], nums[1])
class Solution {
public int rob(int[] nums) {
if(nums.length==0){
return 0;
}
if(nums.length==1){
return nums[0];
}
int[] result=new int[nums.length];
result[0]=nums[0];
result[1]=Math.max(nums[0],nums[1]);
for(int i=2;i<nums.length;i++){
result[i]=Math.max(result[i-1],result[i-2]+nums[i]);
}
return result[nums.length-1];
}
}