数据结构笔记第一章：绪论

第一章：绪论

1. 考研中算法设计的代码规范等基础知识

1.1 书写规范

① 不写 宏定义 #define、头文件 #include、主函数 int main()

② 只写功能函数

1.2 C/C++ 中结构体与指针

1.2.1 结构体

一种可以混合类型的“数组”

1.2.1.1 举例

struct Node    //结构体名称
{
    int a;
    char b;	    // 类型可以不同
    float c;
};  //这里分号不要忘记

1.2.1.2 关于typedef（起小名）

eg:

#define OK 1
#define ERROR 0
typedef int Status;	    //相当于给int起一个小名

1.2.2 指针

指针型变量装的是变量的地址，也称为“指向某个变量”

int *a;
float *b;
struct Node *c;	    //表示定义了某某类型的指针
// (int *)、(float *)…

p = &x;    //对x变量取地址，并存于指针变量p中
*p;    //访问p所存地址对应变量的内容  (这里指x的内容)

考研中指针类型最常使用于和结构体结合构造结点：

1.2.3 构造结点

1.2.3.1 链表结点

typedef struct Node
{
    int data; // 数据域
    struct Node *pNext;    //指针域
}Node,*pNode;	    //起两个小名，一个是struct Node型，
                          //另一个是 struct Node*型

1.2.3.2 二叉树结点

typedef struct BTNode
{
    int data;
    struct BTNode *lChild;    //指向左孩子
	    struct BTNode *rChild;    //指向右孩子
}BTNode,*pBTNode;	    //*pBTNode有无皆可

1.2.3.3 结构体中内容的表示

pNode p;
Node L;		    //以下三种表示等价；
x = p->data;
x = (*p).data;
x = L.data;    

指针用“指”( -> )，结点用“点”( . )

1.2.3.4 malloc()函数

① 为结点申请内存空间

eg: BT = (BTNode *) malloc(sizeof(BTNode));

(强制转换为BTNode *类型)，(BT出来就是指向一个BTNode 大小的指针)

② 动态申请数组空间

eg: p = (int *)malloc(sizeof(int)*n);

注意： malloc申请的内存，要用free()释放掉

1.3 函数

这里使用的是C++中的引用，说白了就是起小名。

因为形参的作用域在函数之内，所以主函数中的变量并不能直接在函数中被改变。

两种解决方案：

① C语言中传入指针：(一般不使用)

void changed(int x, int y)
{
    int temp;
    temp = x;
	    x = y;
    y = temp;
    return;
}    //并不能交换x,y 的值

void changed(int *x,int *y)
{
    int temp;
    temp = *x;
    *x = *y;
    *y = temp;
    return;
}    //可以交换x,y 的值

② C++中引用：（推荐使用）

void changed(int &x, int &y);

注意：这里的"&"，并不是C中的取地址符，而是指引用型

③ 使用技巧：

只要参数在函数中被改变，就要使用&

(除数组外，数组不需要使用&，其他参数，只要被改变都要用&，比如：改变指针的指向，就是 *&x)

2. 基本概念

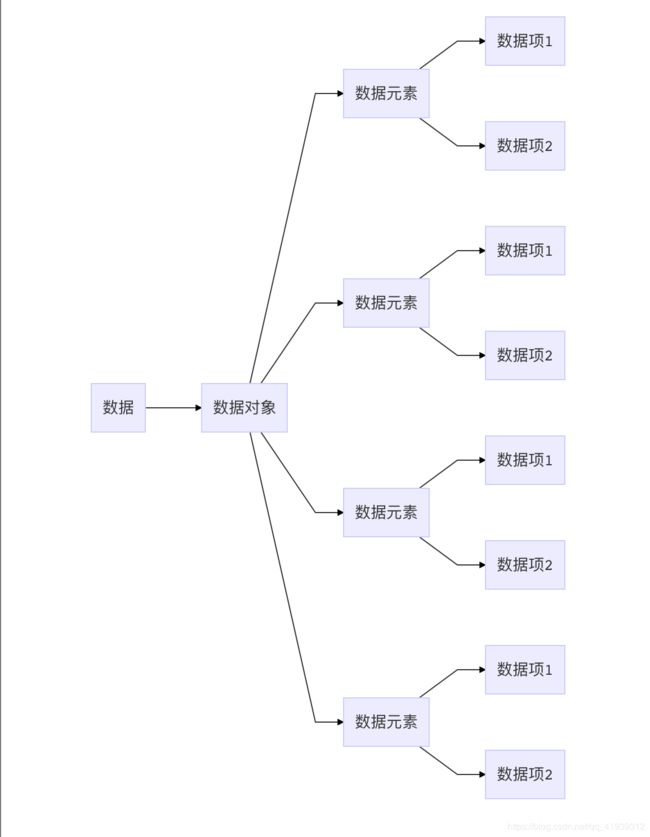
2.1 数据

描述客观事物，计算机可识别和处理的符号集合；

2.2 数据元素

组成数据的、有意义的基本单位；（即 ：记录）

2.3 数据项

组成数据元素，且是最基本、不可分割的最小单位；（即：属性）

2.4 数据对象

具有相同性质的数据元素的集合；

2.5 数据结构

存在特定关系的元素的集合；

2.6 数据类型

① 原子型：不可再分

② 结构型：可再分

③ 抽象数据类型(ADT)：抽象数据组织和相关操作；（由数据对象、数据关系、基本操作集构成）

概念之间关系：

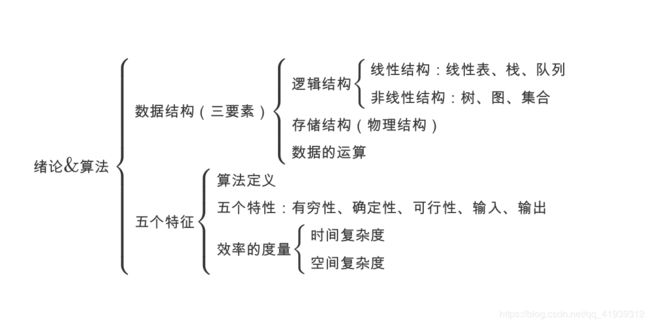
2.7 数据结构三要素

2.7.1 数据的逻辑结构

数据对象中，数据元素之间的关系

模型

① 集合结构：在一个集合中，无其他关系；

② 线性结构：元素之间一对一的关系；

③ 树形结构： 元素之间一对多的关系；

④ 图形结构：元素之间多对多的关系；

2.7.2 数据的存储结构（物理结构）

逻辑结构在计算机中的存储形式

具体工具

① 顺序结构：数据元素存放在连续的存储单元中；

② 链式结构：存储单元可连续，可不连续，上一个结点存放下一个结点的地址信息；

③ 索引结构：一般形式—> <关键字, 地址>；

④ 散列存储：用散列函数（哈希函数）计算结点的存储地址；

2.7.3 数据的运算

运算的定义针对逻辑结构，运算的实现针对存储结构；

2.7.4 注意事项

① 易错点：分不清哪些是逻辑结构，哪些是存储结构。

如：逻辑结构的一些例子：线性表（可以用顺序表或链表实现），栈和队列（可以用顺序存储和链式存储实现），二叉树、有向图、集合等；

即：逻辑结构可以采用多种存储结构实现

② 逻辑结构面向实际问题，抽象表达，独立于存储结构；

而存储结构指逻辑结构在计算机中的映射，不能独立于逻辑结构而存在；

3. 算法及算法评价

3.1 算法

解决特定问题求解步骤的描述，指令的有限序列

3.2 算法的特性

① 有穷性：执行步骤必须有限，每步必须在有限时间内完成；

② 确定性： 含义明确，无二义；（即 对相同的输入，只得到相同的输出）

③ 可行性；

④ 输入：可有零个或多个输入；

⑤ 输出：可有一个或多个输出；

3.3 算法的设计要求

正确性、可读性、健壮性、高效率和低存储；

3.4 算法的度量

3.4.1 时间复杂度

这里是指算法中基本操作的执行次数，而非执行时间

3.4.1.1 基本操作

基本操作一般是指最深层循环内的语句

3.4.1.2 时间复杂度的选取

时间复杂度分为：最好情况，平均情况，最坏情况；

一般选取最坏情况作为基本度量；

3.4.1.3 公式

$T(n)=O(f(n))$

其中大O阶公式如下处理：

① 写出 $f(n)$

eg: $f(n)=2n^3+4n^2+7n+1000$

② 保留 $\mathbf{n}$ 增长最快的阶，并把系数取 $1$

eg: $T(n)=O(f(n))=O(n^3)$

增长速度：（由慢到快）

$\mathbf{O}(1)<\mathbf{O}(\log \mathbf{n})<\mathbf{O}(\mathbf{n})<\mathbf{O}(\mathbf{n}\log \mathbf{n})<\mathbf{O}({\mathbf{n}}^2)<\mathbf{O}({\mathbf{n}}^3)<\cdots <\mathbf{O}({\mathbf{n}}^{\mathbf{k}})<\mathbf{O}(2^{\mathbf{n}})<\mathbf{O}(\mathbf{n}!)<\mathbf{O}({\mathbf{n}}^{\mathbf{n}})$

3.4.2 空间复杂度

算法运行时，对所需存储空间的度量，主要考虑临时占用的存储空间的大小

算法原地工作是指算法所需的辅助空间为常量，即$\mathbf{O}(1)$