【图结构】meta-graph相似度计算
作者:張張張張
github地址:https://github.com/zhanghekai
【转载请注明出处,谢谢!】
文章目录
- meta-graph相似度计算
- 1. meta-graph的定义
- 2. 与meta-path相比
- 3.meta-graph相似矩阵计算
- 4. 拓展
meta-graph相似度计算
1. meta-graph的定义
\qquad m e t a − g r a p h M meta-graph\;M meta−graphM是一个使用单个源节点 n s n_s ns和单个目标节点 n t n_t nt的有向无环图( n s n_s ns的入度为 0 0 0, n t n_t nt的出度为 0 0 0)。定义一个异构信息网络 G = ( V , E ) G=(V,\Epsilon) G=(V,E),它的网络模式为 T G = ( A , R ) \Tau_G={(A,R)} TG=(A,R),其中 V V V是节点的集合, E \Epsilon E是边的集合, A A A是节点类型的集合, R R R是边类型的集合,于是我们定义一个 m e t a − g r a p h meta-graph meta−graph为 M = ( V M , E M , A M , R M , n s , n t ) M=(V_M,\Epsilon_M,A_M,R_M,n_s,n_t) M=(VM,EM,AM,RM,ns,nt),其中 V M ⊆ V V_M\subseteq V VM⊆V, E M ⊆ E \Epsilon_M\subseteq \Epsilon EM⊆E分别受到 A M ⊆ A A_M\subseteq A AM⊆A, R M ⊆ R R_M\subseteq R RM⊆R的约束。
2. 与meta-path相比
\qquad 我们使用两条 m e t a − g r a p h / m e t a − p a t h meta-graph/meta-path meta−graph/meta−path来说明计算问题。
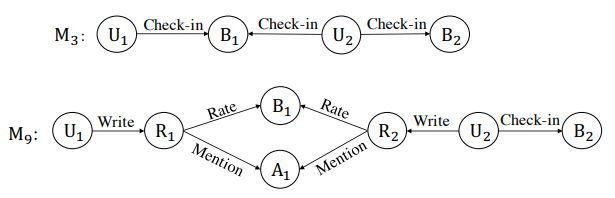
\qquad 在 M 3 M_3 M3、 M 9 M_9 M9中, U ( u s e r ) U(user) U(user)作为源节点 n s n_s ns, B B B(Yelp中的业务)作为目标节点 n t n_t nt。给定上面的 m e t a − g r a p h meta-graph meta−graph定义,我们想要计算源节点和目标节点之间的相似性。
\qquad 最初,交换矩阵 ( c o m m u t i n g m a t r i x ) (commuting\;matrix) (commutingmatrix)被用来计算元路径的基于计数的相似矩阵,假设我们有一条 m e t a − p a t h P = ( A 1 , A 2 , ⋯ , A l ) meta-path\;P=(A_1,A_2,\cdots,A_l) meta−pathP=(A1,A2,⋯,Al),其中 A i A_i Ai是包含在 A A A中的节点类型。然后我们可以定义一个矩阵 W A i A j W_{A_iA_j} WAiAj视为类型 A i A_i Ai和类型 A j A_j Aj之间的邻接矩阵( a d j a c e n c y m a t r i x adjacency\;matrix adjacencymatrix),于是路径 P P P的交换矩阵为 C P = W A 1 A 2 ⋅ W A 2 A 3 ⋅ . . . ⋅ W A l − 1 W l C_P=W_{A_1A_2}\cdot W_{A_2A_3}\cdot...\cdot W_{A_{l-1}W_l} CP=WA1A2⋅WA2A3⋅...⋅WAl−1Wl。例如,对于 M 3 M_3 M3来说, C M 3 = W U B ⋅ W U B T ⋅ W U B C_{M_3}=W_{UB}\cdot W_{UB}^T\cdot W_{UB} CM3=WUB⋅WUBT⋅WUB,其中 W U B W_{UB} WUB是类型 U U U和类型 B B B之间的邻接矩阵。这表明 m e t a − p a t h meta-path meta−path的基于计数的相似性可以通过向上面的 W U B W_{UB} WUB那样的矩阵序列的乘法来计算。实际上,如果邻接矩阵 W W W是稀疏的,我们可以以非常有效的方式实现这一点。
3.meta-graph相似矩阵计算
\qquad 对于 m e t a − g r a p h meta-graph meta−graph问题变得更加复杂。例如 M 9 M_9 M9所示,这里有两种方法可以通过 m e t a − g r a p h meta-graph meta−graph: ( U , R , A , R , U , B ) (U,R,A,R,U,B) (U,R,A,R,U,B)和 ( U , R , B , R , U , B ) (U,R,B,R,U,B) (U,R,B,R,U,B)请注意, R R R表示 H I N HIN HIN中的实体类型“评论”( R e v i e w Review Review)。在路径 ( U , R , A , R , U , B ) (U,R,A,R,U,B) (U,R,A,R,U,B)中的 ( R , A , R ) (R,A,R) (R,A,R)意味着如果两个评论都提到相同的 A A A(方面, A s p e c t Aspect Aspect),那么它们有一些相似性。同样,在路径 ( U , R , B , R , U , B ) (U,R,B,R,U,B) (U,R,B,R,U,B)中的 ( R , B , R ) (R,B,R) (R,B,R)意味着如果两个评论都评价相同的 B B B(业务, B u s i n e s s Business Business),那么它们也有一些相似性
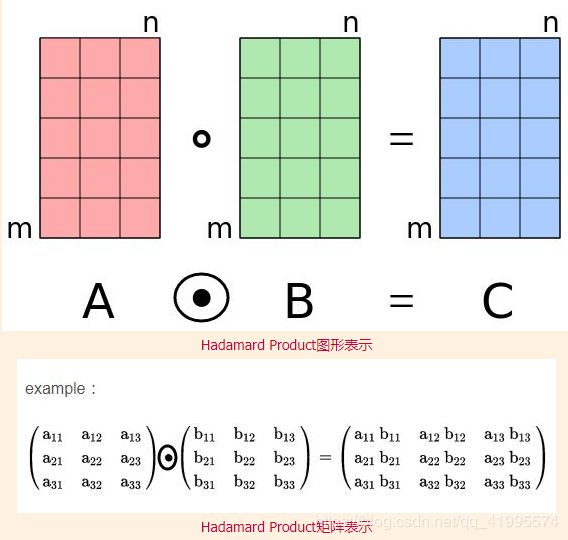
\qquad 当 m e t a − g r a p h meta-graph meta−graph中有从多种从源节点到目标节点方式时,我们应该定义相似逻辑。当有两条路径时:(1)我们可以允许流通过任一路径;(2)约束流通以同时满足这两条路径。通过对第(1)种策略的分析,我们发现它类似于简单地将这种 m e t a − g r a p h meta-graph meta−graph分割成多个元路径,然后再采用之后我们介绍的计算方法。因此,我们选择后者,后者比简单的矩阵乘法需要更多的矩阵运算(即 H a d a m a r d Hadamard Hadamard积或元素相关积)。
\qquad 算法 1 1 1描述了用于计算 M 9 M_9 M9的基于计数的相似性的算法。其中 ⨀ \bigodot ⨀表示 H a d a m a r d Hadamard Hadamard积,在获得 C S r C_{S_r} CSr之后,通过矩阵序列的乘法更容易获得整个交换矩阵 C M 9 C_{M_9} CM9。

★为什么要使用 H a d a m a r d Hadamard Hadamard积来解决 m e t a − g r a p h meta-graph meta−graph中出现的分叉式转移概率计算?
\qquad C P 1 C_{P_1} CP1和 C P 2 C_{P_2} CP2分别表示各自两种路径下从 R R R到 R R R的转移概率( R R R为节点类型 R e v i e w Review Review)。两种转移概率进行 H a d a m a r d Hadamard Hadamard积,实际上就是取逻辑里的“与”关系(两条路径只要有一条路径转移概率为 0 0 0,那么综合的转移概率还是 0 0 0, H a d a m a r d Hadamard Hadamard积正好可以满足这一点),因为本质上 m e t a − g r a p h meta-graph meta−graph分叉的地方,都是需要同时满足的。
\qquad 通过计算沿着 m e t a − g r a p h M meta-graph\;M meta−graphM的所有 u s e r user user和 i t e m item item之间的相似性,我们可以获得 u s e r − i t e m user-item user−item相似性矩阵 R ^ ∈ R m × n \hat{R}\in R^{m\times n} R^∈Rm×n,其中 R ^ i j \hat{R}_{ij} R^ij表示沿着 m e t a − g r a p h M meta-graph\;M meta−graphM的 u s e r u i user\;u_i userui和 i t e m b j item\;b_j itembj之间的相似性, m m m和 n n n分别是 u s e r user user和 i t e m item item的数量。然后通过设计 L L L个 m e t a − g r a p h meta-graph meta−graph,我们可以得到 L L L个不同的 u s e r − i t e m user-item user−item相似性矩阵,用 R 1 , R 2 , ⋯ , R L R_1,R_2,\cdots,R_L R1,R2,⋯,RL表示。
4. 拓展
\qquad 如果我们的 m e t a − g r a p h meta-graph meta−graph矩阵是对称的,如下图所示:
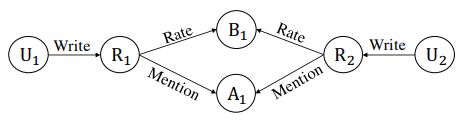
\qquad 那么我们得到交换矩阵( c o m m u t i n g m a t r i x commuting \;matrix commutingmatrix)后,可以使用 P a t h S i m PathSim PathSim,对其进行相似度计算(可以理解为交换矩阵的归一化),公式如下:
S ( x i , x j ) = 2 M i j M i i + M j j S(x_i,x_j)=\frac{2M_{ij}}{M_{ii}+M_{jj}} S(xi,xj)=Mii+Mjj2Mij
其中 M M M为上一小节中计算得到的 m e t a − g r a p h meta-graph meta−graph交换矩阵。
该相似矩阵满足以下两条性质:
- 对称性: S ( x i , x j ) = S ( x j , x i ) S(x_i,x_j)=S(x_j,x_i) S(xi,xj)=S(xj,xi)
- 自我相似性最高: S ( x i , x j ) ∈ [ 0 , 1 ] , a n d S ( x i , x i ) = 1 S(x_i,x_j)\in [0,1],and\;S(x_i,x_i)=1 S(xi,xj)∈[0,1],andS(xi,xi)=1
【参考文献】
- Meta-Graph Based Recommendation Fusion over Heterogeneous Information Networks
- Hadamard Product