BiCycleGAN——Toward Multimodal Image-to-Image Translation，NIPS2017论文解读

论文亮点

1、提出可以生成更具多样性样本的BiCycleGAN框架，确保输入噪声向量与输出图像的双向映射一致性，即隐层向量和输出图像的关系是可逆的。
2、相比pix2pix、CycleGAN等模型，作者鼓励输出和潜层空间有双向映射。双向映射指的是不仅可以有潜层编码（输入噪声）到输出生成图像的映射，还有从生成图像返回到潜层编码的映射。并且确保初始的潜层编码（正向映射中）和返回的潜层编码（反向映射中）一致，这样就能解决不同的输入对应相同的生成图像的问题 （模式崩溃），由一对多的映射变回一对一的映射。
3、不同于CycleGAN的是，BicycleGAN仍然需要成对的图像作为输入。

摘要

  许多图像到图像的翻译任务都是定义模糊的，比如单个输入图像可能需要对应多个可能的输出。在这些工作中，我们致力于在条件生成对抗网络的设定下（即输入不仅仅是噪声，还有条件变量），对可能的输出分布进行建模。映射的模糊性（即实现单输入——多输出）体现在低维隐层向量中，而隐层向量在测试中随机采样。生成器学习将给定输入与这种隐层向量相结合，并将其映射到输出中。我们明确鼓励输出和隐层向量之间的关系是可逆的。这可以帮助避免在训练阶段，隐层向量合成输出时的多对一映射，也被称为“模式崩溃”问题，并且可以产生更具多样性的结果。我们通过应用不同的训练目标、网络结构和加入隐层编码（即噪声）的方式，探索了几种这个方法的变体。我们提出的方法鼓励隐层编码和输出图像的双射一致性。在感知真实性和多样性的方面，展示了一个我们方法和其他变体的系统比较。

介绍

  之前大部分有条件的图像生成工作专注于生成单种结果。在这项工作中，我们对潜在结果的分布进行建模，因为许多问题在自然界中都是多模态的（即单种输入可能对应于多个输出）。如下图所示，晚上拍摄的图像看起来和白天的很不一样，取决于云的模式和光线条件。我们的目标有两个：（1）在感知上逼真；（2）生成结果具有多样性。

  上图展示了使用作者提出的方法进行的多模态图像到图像转换。给定来自一个域（一个场景的晚上图像）的一张输入图像，我们试图建模目标域（相应场景的白天图像）的潜在输出分布，生成逼真而又多样的结果。
  将一个高维输入分布映射到一个高维输出分布是很具挑战性的。用于表示多模态（即使输出图像多样化，如图1）常见的方法是学习一个低维隐层编码，这个隐层编码应该可以表示可能的而又不包括在输入中的输出图像。在推理阶段，确定性的生成器使用输入图像和随机采样的隐层编码，来随机地生成采样输出。已存在方法中的一个共同问题是模式崩溃，其中只有一小部分的真实样本被表现在了网络输出中（即输出结果的多样性非常差）。作者系统地研究了一些方法来解决这个问题。
  我们从$pix2pix$模型开始，$pix2pix$的作者注意到仅仅加入一个随机抽取的隐层编码并不会产生多样性的结果。作为改进，我们鼓励输出图像和隐层空间有双向映射。我们不仅执行从隐层编码（和输入一起）到输出图像的映射，还学习了一个从输出图像返回到隐层空间的编码器。于是，这种方式不会鼓励有两个可以生成相同输出图像的隐层编码存在。在训练中，学习到的编码器试图传递足够的信息给生成器，来解决关于输出模式的任何模糊性。例如，当从一个夜晚图像生成一个白天图像时，隐层向量可以是关于天空的颜色、在地面的光线影响或是云的特征的信息的编码(在训练中由编码器进行，测试时没有编码器，生成器直接从隐层空间随机采样)。有序地组合编码器和生成器可以恢复相同的图像（即cVAE-GAN），而反过来组合则会产生相同的潜层编码（cLR-GAN）。
  受到无条件生成模型的启发，在这项工作中，我们通过探索几种目标函数来说明这个想法：

1. cVAE-GAN（Conditional Variational Autoencoder GAN）——在训练阶段中，先将真实图像（即输出图像）编码到隐层空间，然后给生成器一个朝着期望输出的“附加噪声”（即编码结果）。使用这个“附加噪声”和输入图像，生成器可以重建特定的输出图像。为了确保在测试阶段可以使用随机采样，对真实图像编码得到的隐层空间分布通过KL散度被正则化为一个标准正态分布（如果不是正态分布，则在测试阶段采样就比较困难，随机采样得到的结果可能和编码分布没有关系）。
2. cLR-GAN（Conditional Latent Regressor GAN）——首先提供了一个随机抽取的隐层向量给生成器。在这个例子中，生成的输出可能看起来不接近真实图像，但是它非常逼真（可能生成逼真但和真实图像无关的内容）。然后编码器试图从输出图像中恢复隐层向量，从而实现隐层向量的自我一致性（为什么要实现？）。这个方法可以被视为“潜层回归”模型的条件形式，和InfoGAN相关。
3. BicycleGAN——最终，我们结合了这两个方法来共同地促进隐层向量和输出图像在两个方向上的连接，并取得了更好的表现。我们展示了我们的方法可以生成具有多样性且视觉上更吸引人的结果，特别是在多样性上超过了其他基准模型，包括往$pix2pix$模型中添加噪声的方法。除了损失函数之外，我们还研究了关于几种编码网络的表现，还有不同的将潜层编码输入到生成器网络的方式。
     我们进行了一个对这些方法的系统评估，通过使用人眼判断和视觉距离度量来评估输出的多样性。代码和数据可在BicycleGAN的Pytorch代码上获取。

相关工作

生成模型

  由受限玻尔兹曼机和自编码器——变分自编码器和自递归模型——GAN发展而来，不再赘言。

条件图像生成

  上述所有生成模型都可以很简单地条件化，只需要在输入中额外加入一个条件变量即可。加入条件变量后，图像的生成质量有了很大的提高。但是这种提高是以降低结果的多样性换取的，因为当加入条件变量后，生成器会在很大程度上忽略随机噪声向量。虽然事实上，有结果显示忽略噪声向量导致了更稳定的训练。

确定编码的多模态

  一种表达多个模态（即多种可能的输出图像）的方式是准确地编码它们，并且将编码结果作为输入图像之外的额外条件输入。例如，颜色和形状或是其他的属性已经被作为一个条件变量用于pix2pix中。在无条件生成中虽然已经取得了某种程度上的成功，但有条件的图像到图像的生成仍然和取得与无条件生成相同的结果相差甚远，除非能准确地对上述提到的进行编码。在这项工作中，我们学习了一个通过加强隐层空间和图像空间的紧密连接来对输出的多种模态进行建模的条件图像生成模型。

多模态的图像到图像转换

  我们的目标是学习一个在两个图像域之间的多模态映射，例如同一场景的白天图像转换到夜晚图像。即从输入域$\mathcal{A}\subset {\mathbb{R}}^{H\times W\times 3}$，映射到输出域$\mathcal{B}\subset {\mathbb{R}}^{H\times W\times 3}$中。在训练中，给出了来自这些域的成对样本$\{(\mathbf{A}\in \mathcal{A},\mathbf{B}\in \mathcal{B})\}$，代表了联合分布$p(\mathbf{A},\mathbf{B})$。需要注意的是，在实际场景中，相对于输入图像A可能会有多个合理的B与之对应，而训练集中的B只不过是其中一个（我们的目标就是合成其他的B）。在测试中，给定一个新的样本$\mathbf{A}$，我们的模型应该会生成输出$\mathbf{B}$的不同集合，对应分布$p(\mathbf{B}|\mathbf{A})$中的不同模态。
  尽管条件GAN在图像到图像的翻译任务中取得了成就，但它们主要受限于当给定输入图像$\mathbf{A}$时，会生成一个确定性的输出$\mathbf{B}$。另一方面，我们也希望学习可以从给定$\mathbf{A}$的真实条件分布中能采样出输出$\mathbf{B}$的映射，并且产生具有多样性和逼真性的结果。为了实现这一点，我们学习了一个低维隐层空间$\mathbf{z}\in {\mathbb{R}}^Z$，它压缩了输出模态中未在输入图像上表示出来的模糊不清的方面。例如，一个鞋子的草图可以被映射成一系列的颜色和纹理，而这些颜色和纹理都可以在潜层编码中被压缩。我们接下来学习一个对于输出的确定性映射
$G:(\mathbf{A},\mathbf{z})\to \mathbf{B}$。为了可以随机采样，我们期望潜层编码向量$\mathbf{z}$可以从一些先验分布$p(\mathbf{z})$中提取，我们在这项工作中使用了标准高斯分布$\mathcal{N}(0,I)$。
  我们首先讨论了一个已存在方法的简单拓展，并且讨论了它的强项和弱点，启发了我们自己的工作，所有的方法都在下图中展出。

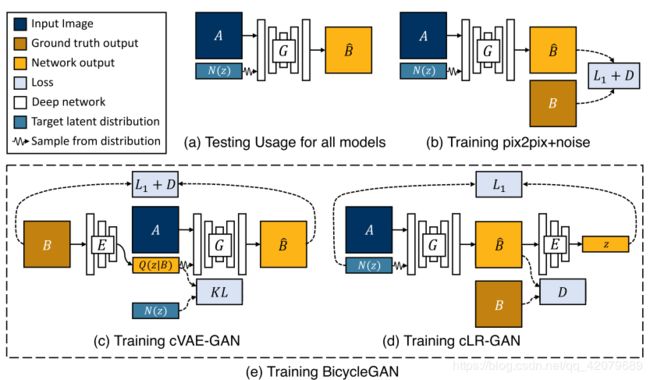
  上图是本文方法的总述（overview）。
  图(a)表述在测试时所有模型的使用方法——为了生成一个样本输出，潜层编码$\mathbf{z}$首先从一个已知分布（例如一个标准正态分布）中随机采样。生成器$G$将输入图像$\mathbf{A}$（蓝色）和潜层编码$\mathbf{z}$映射到一个输出样本$\mathbf{B}$（黄色）上。
  图(b)表述了$pix2pix+noise$的baseline模型，$\mathbf{B}$（棕色）表示对应于$\mathbf{A}$的真实图像。
  图(c)表述了$cVAE-GAN$模型，它从前一个真实目标图像$\mathbf{B}$开始，将它编码到潜层空间。生成器随后尝试着将输入图像$\mathbf{A}$和采样的$\mathbf{z}$（这个z是从编码结果中采样的，而不是噪声正态分布中采样的。在后面，作者讨论了还从噪声正态分布中采样的情况，即cVAE-GAN++）映射回原始图像$\mathbf{B}$。
  图(d)表述$cLR-GAN$模型，它随机地从一个已知分布中采样潜层编码$\mathbf{z}$，并将它和输入图像$\mathbf{A}$一起映射到输出图像$\mathbf{B}$，随后尝试着从输出中重建潜层编码。
  图(e)表述了作者提出的$BicycleGAN$方法，结合了两个方向上的限制。

Baseline:pix2pix+noise$(\mathbf{z}\to \mathbf{B})$

  pix2pix模型的作者在实验过程中发现生成器在很大程度上会忽略噪声，因此他最后并没有采用输入噪声，而是用了Dropout的形式。这在很多有条件的生成实验中也被观测到，在无条件实验中则被称为模式崩溃问题。在这个实验中，我们探索了几种不同的方式来解决这个问题。

Conditional Variational Autoencoder GAN:$\mathrm{c}\mathrm{V}\mathrm{A}\mathrm{E}-\mathrm{G}\mathrm{A}\mathrm{N}(\mathrm{B}\to \mathrm{z}\to \mathrm{B})$

  一种迫使潜层编码$\mathbf{z}$“有用”的方式是直接通过编码器$E$将一个真实图像$\mathbf{B}$映射到潜层编码。然后生成器$G$可以使用潜层编码和输入图像$\mathbf{A}$一起合成期望输出$\mathbf{B}$。整个模型可以简单地理解为$\mathbf{B}$的重建，生成器的输入是潜层编码$\mathbf{z}$和输入图像$\mathbf{A}$的级联。
  这种方法在无条件场景的VAE取得了成功。将它扩展到有条件场景下，通过编码器$E$得到的潜层编码需要符合高斯分布假设（使用重采样技巧）。
  作者在本文中使用的GAN的损失函数为：
$${\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}^{\mathrm{V}\mathrm{A}\mathrm{E}}={\mathbb{E}}_{\mathbf{A},\mathbf{B}\sim p(\mathbf{A},\mathbf{B})}[\log (D(\mathbf{A},\mathbf{B}))]+{\mathbb{E}}_{\mathbf{A},\mathbf{B}\sim p(\mathbf{A},\mathbf{B}),\mathbf{z}\sim E(\mathbf{B})}[\log (1-D(\mathbf{A},G(\mathbf{A},\mathbf{z})))]$$
  需要注意的是，这与原始的VAE-GAN损失函数不同，没有包括从先验分布$p(z)$中采样得到的生成图像的损失，而只有从$E(x)$得到的编码中采样得到的重建图像损失，作者在后面也讨论了加入从先验分布$p(z)$中采样得到的生成图像的损失，称之为VAE-GAN++。
  另外两个损失项还包括编码器得到的编码要接近标准正态分布的KL损失，以及编码-解码（生成）过程后的重建损失，最后，cVAE-GAN的总损失为：
$$G^{\ast },E^{\ast }=\arg \underset{G,E}{\min }\underset{D}{\max }{\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}^{\mathrm{V}\mathrm{A}\mathrm{E}}(G,D,E)+\lambda {\mathcal{L}}_1^{\mathrm{V}\mathrm{A}\mathrm{E}}(G,E)+{\lambda }_{\mathrm{K}\mathrm{L}}{\mathcal{L}}_{\mathrm{K}\mathrm{L}}(E)$$
  作者还考虑了cVAE-GAN的确定性情况，即不在损失函数中加入要求编码器得到的编码接近标准正态分布这一项，称之为cAE-GAN。然而，由于cAE-GAN在潜层空间$\mathbf{z}$上的分布无法确保，在测试的时候对其进行采样会比较困难。

Conditional Latent Regressor GAN:cLR-GAN$(\mathbf{z}\to \hat{\mathbf{B}}\to \mathbf{z})$

  作者探索了另一种方法来迫使生成器网络利用隐层编码。如上图中(d)所示，从一个随机抽取的隐层编码$\mathbf{z}$上开始，并且尝试着通过$\mathbf{z}=E(G(\mathbf{A},\mathbf{z}))$将它进行重建。
  需要特别注意的是，这里的编码器$E$编码得到的是一个$\mathbf{z}$的点估计，而在之前的VAE-GAN中编码器产生的是一个$\mathbf{z}$的高斯分布估计。所谓的点估计即可以逐点计算其损失（L1 Loss），而分布估计则需要用KL散度去度量两分布之间的差距。
$${\mathcal{L}}_1^{\text{latent }}(G,E)={\mathbb{E}}_{\mathbf{A}\sim p(\mathbf{A}),\mathbf{z}\sim p(\mathbf{z})}\Vert \mathbf{z}-E(G(\mathbf{A},\mathbf{z})){\Vert }_1$$
  我们也引入了判别器损失来使网络生成更为逼真的结果，总损失函数可以写为：
$$G^{\ast },E^{\ast }=\arg \underset{G,E}{\min }\underset{D}{\max }{\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}(G,D)+{\lambda }_{\text{latent }}{\mathcal{L}}_1^{\text{latent }}(G,E)$$
  在cLR-GAN中，关于生成图像和真实图像的L1 Loss没有使用。因为噪声向量是随机选取的，所以生成图像$\mathbf{B}$不需要和真实图像过于相似，只需要逼真即可。

Our Hybrid Model:BicycleGAN

  作者结合了cVAE-GAN和cLR-GAN形成了一个混合模型。对于cVAE-GAN来说（缺点），在训练阶段是从真实数据进行编码的，但是在测试阶段随机隐层编码不一定可以生成逼真的图像——KL散度可能没有最优化。更重要的是，判别器$D$并没有机会在训练过程中见到来自先验分布$p(z)$生成的结果（在cVAE-GAN中不可见，在cVAE-GAN++中可见）。在cLR-GAN中（缺点），隐层向量可以很容易从一个简单分布中采样得到（不需要像VAE-GAN一样先对真实图像进行编码），但是生成器并没有通过观察真实的输入-输出对所带来的好处进行训练（没有L1 Loss等，可能生成逼真的，但和真实图像无关的结果）。我们提出在两个方向$\mathbf{B}\to \mathbf{z}\to \hat{\mathbf{B}}$ and $\mathbf{z}\to \hat{\mathbf{B}}\to \mathbf{z}$上进行训练，目的是利用两种循环的优点，因此取名为BicycleGAN。
$$\begin{array}{rl}{G}^{\ast },E^{\ast }=\arg {\min }_{G,E}{\max }_D& {\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}^{\mathrm{V}\mathrm{A}\mathrm{E}}(G,D,E)+\lambda {\mathcal{L}}_1^{\mathrm{V}\mathrm{A}\mathrm{E}}(G,E)\\ & +{\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}(G,D)+{\lambda }_{\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}}{\mathcal{L}}_1^{\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}}(G,E)+{\lambda }_{\mathrm{K}\mathrm{L}}{\mathcal{L}}_{\mathrm{K}\mathrm{L}}(E)\end{array}$$
其中超参数$\lambda$、${\lambda }_{latent}$和${\lambda }_{KL}$控制了每一项的相对重要性。
  在无条件GAN的生成中，VAE-GAN的作者观察到了同时使用来自先验分布$N（0,1）$和编码器生成分布的样本可以进一步提升结果。因此，作者也使用了这种变体，称之为cVAE-GAN++，它可以使判别器看见从先验分布中随机选取的样本。

实施细节

网络结构

  对于生成器$G$，作者使用了U-Net框架，其中包含了编码器-解码器结构，以及对称的跳跃连接。当输入和输出有空间对应性时，U-Net结构已经被证明了可以在单向图像预测上产生很好的结果。对于判别器$D$，我们在不同的尺度上使用了两个PatchGAN，用于判别$70\times 70$和$140\times 140$的区域是真或假。对于编码器E，我们用两种网络进行了实验：（1）$E_{CNN}$：带有一些卷积层和下采样层的CNN；（2）$E_{ResNet}$：带有一些残差块的分类器。

训练细节

  我们基于LSGAN的变体搭建了我们的模型，其中使用了最小均方损失代替交叉熵损失。LSGAN可以通过稳定的训练，生成更高质量的图像。我们也发现在判别器上不添加条件输入（即输入图像$A$）可以产生更好的结果。相比共享权重，我们发现使用两个分开的判别器可以取得更好的视觉结果。对于cLR-GAN中隐编码与它重建结果的L1 Loss（注意只有这一个Loss是单独更新G），我们单独更新G，因为我们发现同时更新G和E的参数会隐藏潜层编码的信息。

注入潜层编码$z$到生成器的方式

  我们探索了两种将潜层编码$z$（噪声）注入到生成器的方式，如下图所示：

  两种方式：将潜层编码$z$（噪声）通过空间复制（成四维张量）和级联注入到编码器的输入层或是编码器（生成器？）的每一层。
  在第一种方式中，我们将潜层编码空间复制为$H\times W\times Z$张量，并将它与$H\times W\times 3$输入图像级联。在第二种方式中，在调整到合适的尺寸后，我们将$z$加入到$G$的每一层。

实验

数据集

  在来自之前工作的一些图像到图像翻译问题上测试了作者提出的模型，这些问题都是一对多映射（one-to-many mappings）。所有的训练图像大小为$256\times 256$。

使用的模型

  评估了上述讨论中提到的模型的表现，包括：【1】pix2pix+noise，【2】cAE-GAN，【3】cVAE-GAN，【4】cVAE-GAN++，【5】cLR-GAN和作者提出的混合模型【6】BicycleGAN。

定性评估

  上图展示了BicycleGAN模型在不同样本下的生成结果。

  上图在labels-facades数据集上，展示了不同模型定性比较的结果。BicycleGAN模型可以产生逼真而又多样性的结果。而pix2pix+noise模型典型地只能产生单一的逼真输出，而没有产生任何有意义的变化。cAE-GAN增加了输出的变化，但是牺牲了结果的质量作为代价。
  我们观察到cVAE-GAN模型的生成结果也有很好的多样性，因为它的潜层空间被鼓励编码关于真实输出的信息。然而，cVAE-GAN模型的潜层空间并不是分布稠密的，因此从中抽取随机样本可能会导致输出中存在伪影。cLR-GAN模型的输出结果的可变性较小，并且有时还会出现模式崩溃。而在混合的BicycleGAN模型中，我们观察到生成的样本既富有多样性，也很逼真。

定量评估

  作者基于上述模型，在Google maps-satellites数据集上进行了关于多样性、逼真性和潜层空间分布的定量分析。

多样性评估

  作者计算了深度特征空间中，随机样本的平均距离。预训练网络曾经被用于计算在图像生成应用中的“perceptual loss”，也可以被用于生成模型中的“验证分数”，例如，评价生成模型的语义质量和多样性，或是评价灰度图像彩色化的语义准确性。

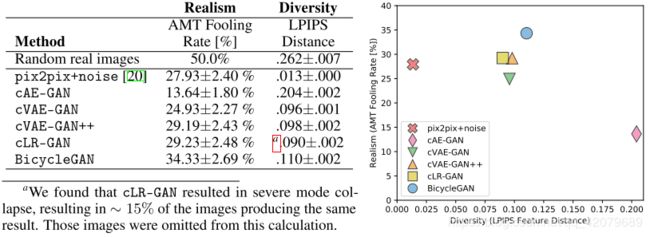
  上图展示了使用LPIPS距离得到的多样性得分。对于每一种模型，我们在1900对随机生成的输出图像$\mathbf{B}$上（采样自100张输入图像$\mathbf{A}$）计算平均距离。在真实图像的随机对上可以计算得到0.262的变化值。pix2pix模型产生了单一的点估计，加入噪声后也没有很大的变化。cAE-GAN模型增加了变化性，其他四个模型都得到了相似的多样性得分，因为它们都对潜层空间做出了明确的限制。我们注意到高多样性得分也可能代表非自然的图像被生成了，这也可能带来一些无意义的多样性变化。因此，作者接下来进行了视觉逼真度量。

感知逼真性评估

  作者找了一些人来进行判断，以人眼判断的错误率作为评价指标。如上一张所示，pix2pix+noise模型可以产生很逼真的图像，但是它的多样性很低。cAE-GAN可以产生多样的图像，但是它产生的图像却不逼真。因为学习到的潜层空间分布是不清晰的，采样的随机样本可能来自于空间的稀疏区域。加入了KL散度的cVAE-GAN提升了视觉逼真性。随后，如期望所示的，检查了随机提取的潜在向量的cVAE-GAN++少量地提升了逼真性（5%）。从预定义的分布随机抽取潜在向量z的cLR-GAN可以达到和cVAE-GAN++相似的逼真性和多样性得分。然而，cLR-GAN模型存在大量的模式崩溃——大约15%的输出产生了相同的结果，与输入图像无关。最后，BicycleGAN模型取得了最优的结果，并且没有出现模式崩溃的问题。

编码器的结构评估

  最终使用了ResNet架构的编码器，而没有使用传统的CNN架构。

注入潜在向量的方式

  上述讨论的两种将潜在向量注入生成器（U-Net）的方式取得了相似的结果，这证明了U-Net结构可以很好地将信息传递给输出，作者最终使用了将潜在向量$z$注入到生成器的所有层的方式。

潜在向量的长度

  在BicycleGAN中，作者研究了潜在向量维度的变化值的影响，其维度取值在$[2,8,256]$。

  其结果如上图所示，一个非常低的维度（比如2）可能会限制结果多样性的表达。相反的，一个非常高的维度则会编码关于输出图像更多的信息，以使得采样困难为代价。最优的潜在向量的长度很大程度上取决于独特的数据集和应用，以及在输出中有多少不确定性。

结论

  作者发现结合多种目标函数来鼓励潜在编码和输出空间之间的双向映射可以获得逼真而又多样性的结果。