网络流最大流-Ford-Fullerson和dinic算法，最小割

网络就是一张带权有向图，把其看作一个输水的管道更直观一点，源点就是整个系统的水源来处，汇点就是水流最后到达的地方。其他的中间点都是闸门，闸门是不会产生和私吞水量的，而每个闸门之间都是由管道连接的，这个管道决定了你能在这个通道中间最大传多少水。每个闸门之间又会交错相连，由此也就有了最大流问题，也就是这个网络最大的流量是多少。
我们还需要知道一个定义：
增广路：从源点找到一条能达到汇点的路，这条路会使总流量增加，就叫做增广路。
找最大流也就是不断的找增广路的过程，直到所有的增广路都被找过。
这个时候可能大家脑海里已经想到了深搜，但深搜的问题还得通过别的方法解决一下，深搜有什么问题呢？
比如

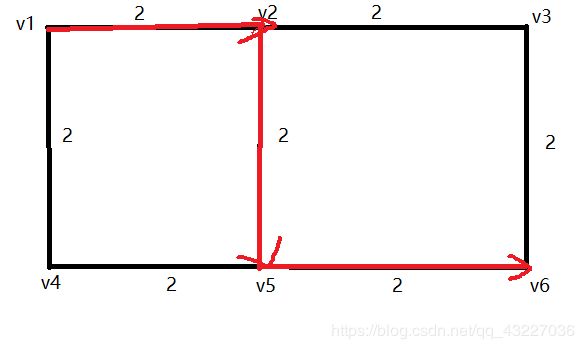
这张图通过深搜肯定会找到v1->v2->v5->v6;
但实际这条路我们并不需要，这个时候就需要给程序一个后悔的机会，能让他把流过去的流量在流回来。因此就有了这个神奇的操作，加一条反向边，如果这条边走过流量f，就把这条边的流量减去f，反向边的流量就加f。

代码如下：

 #include 
#include 
#include  
#include  
#include 

using namespace std;

const int MAX_V = 500001;
const int INF = 0x3f3f3f3f;

struct edge
{
	//终点，容量，反向边 
	int to, cap, rec;
};

struct Node
{
	int from, to;
};

vector p;
vector G[MAX_V];
bool used[MAX_V];

//增加一条从s到t容量为cap的边
void add_edge(int from, int to, int cap)
{
	//正向边，反向边应是第i+1条边，但数组是从0开始的，因此直接加to的size即可
	G[from].push_back((edge){to, cap, G[to].size()});
	//本来应该是第i条边是反向边，但是上面push后size变为了i+1，因此需要减去1
	G[to].push_back((edge){from, 0, G[from].size()-1});
} 

//用dfs寻找增广路
int dfs(int v, int t, int f)
{
	if (v == t)
	{
		return f;
	}
	
	used[v] = true;
	
	for (int i=0; i 0)
		{
			int d = dfs(e.to, t, min(f, e.cap));
			
			if (d > 0)
			{
				e.cap-=d;
				G[e.to][e.rec].cap+=d;
				return d;
			}
		}
	}
	
	return 0;
}

int max_flow(int s, int t)
{
	int flow = 0;
	
	while (1)
	{
		memset(used, 0, sizeof (used));
		
		int f = dfs(s, t, INF);
		
		if (f == 0)
		{
			return flow;
		}
		
		flow+=f;
	}
}

int main()
{
	int n, m;
	
	cin >> n >> m;
	
	for (int i=0; i> a >> b >> cost;
		
		add_edge(a, b, cost);
	}
	
	cout << max_flow(1, n) << endl;
	
	return 0;
} 

我们一般打题都用Dicnic，因为它要比FF快好多
明白了For-Fullerson算法后，Dicnic算法就简单多了，Dicnic算法就是进行一步预处理，通过BFS将图先进行分层操作，然后再用DFS查找增广路。分层后，进行DFS时，只找level高的节点进行深搜，减少了许多不必要的分支。然后其他就都差不多了。
代码如下：

#include 
#include 
#include 
#include 

using namespace std;

const int MAX_N = 500001;
const int INF = 0x3f3f3f3f;

struct edge
{
	int to, cap, rev;
};

vector G[MAX_N];
int level[MAX_N];

void add_edge(int from, int to, int cap)
{
	G[from].push_back((edge){to, cap, G[to].size()});
	//创建反向边
	G[to].push_back((edge){from, 0, G[from].size()-1});
}

void bfs(int s)
{
	memset(level, -1, sizeof(level));
	
	queue que;
	level[s] = 0;
	que.push(s);
	
	while (!que.empty())
	{
		int v = que.front();
		
		que.pop();
		
		for (int i=0; i 0 && level[e.to] < 0)
			{
				level[e.to] = level[v] + 1;
				que.push(e.to);
			}
		}
	}
}

int dfs(int v, int t, int f)
{
	if (v == t)
	{
		return f;
	}
	
	for (int i = 0; i < G[v].size(); i++)
	{
		edge &e = G[v][i];
		
		if (e.cap > 0 && level[v] < level[e.to])
		{
			int d = dfs(e.to, t, min(f, e.cap));
			
			if (d > 0)
			{
				e.cap -= d;
				G[e.to][e.rev].cap += d;
				return d;
			}
		}
	}
	
	return 0;
}

int max_flow(int s, int t)
{
	int flow = 0;
	
	for (;;)
	{
		bfs(s);
		
		if (level[t] < 0)
		{
			return flow;
		}
		
		int f;
		
		while ((f = dfs(s, t, INF)) > 0)
		{
			flow+=f;
		}
	}
}

int main()
{
	int n, m;
	
	cin >> n >> m;
	
	for (int i=0; i> a >> b >> cost;
		
		add_edge(a, b, cost);
	}
	
	cout << max_flow(1, n) << endl;
	
	return 0;
}

然后就是最小割了，为什么在最大流这里面写最小割呢？
二者其实就是一个东西，什么是最小割，就是切断一些边把两个点变得没有一点联系（切断的代价与权值相等），无法通过其中一个点到达另一个点。有一个定理就是最大流等于最小割。所以求最小割的话，就跑一遍最大流就行。