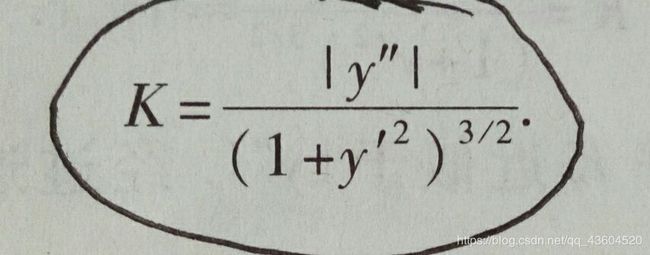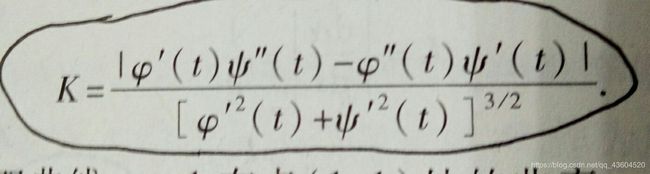- 《高等数学》(同济大学·第7版)第十二章 无穷级数 第四节函数展开成幂级数
一、泰勒级数与麦克劳林级数泰勒多项式与泰勒级数泰勒多项式:若函数f(x)在点x_0处具有直到n阶的导数,则可以构造一个n次多项式:P_n(x)=f(x_0)+f’(x_0)(x-x_0)+[f’'(x_0)/2!](x-x_0)^2+…+[f^(n)(x_0)/n!](x-x_0)^n这个多项式是f(x)在x_0处的最佳逼近多项式。泰勒级数:当n→∞时,若泰勒多项式的余项R_n(x)→0,则f(x
- 《高等数学》(同济大学·第7版)第十二章 无穷级数 第五节函数的幂级数展开式的应用
没有女朋友的程序员
高等数学
一、幂级数展开的核心作用幂级数展开不仅是理论工具,更是解决实际问题的计算利器,主要应用包括:近似计算:用多项式逼近复杂函数(如计算函数值、积分值)。求解微分方程:将解表示为幂级数形式,逐项代入方程求解。求和与积分:将难以处理的级数转化为已知函数的展开式。分析函数性质:通过展开式研究函数的极值、拐点等。二、典型应用详解近似计算函数值原理:用泰勒多项式的前几项近似代替原函数。关键步骤:写出函数的麦克劳
- 《高等数学》(同济大学·第7版)第七章 微分方程 第四节一阶线性微分方程
没有女朋友的程序员
高等数学
好的,这是将您提供的高等数学教案内容中的LaTeX公式转换为纯文本格式后的版本:同学们好!今天我们学习《高等数学》第七章第四节“一阶线性微分方程”。这是一阶微分方程中最重要、应用最广泛的一类方程,掌握它的解法对后续学习(如微分方程的应用、高阶线性微分方程)至关重要。我会用最通俗的语言,结合大量例子,帮你彻底掌握“一阶线性微分方程”的定义、解法和核心思想。一、一阶线性微分方程的定义:长什么样?1.标
- 蔡高厅老师 - 高等数学-阅读笔记 - 01 - 前言、函数【视频第01、02、03、】
Franklin
数学线性代数
高等数学前言;196学时,每周6课主要内容:上册一元、多元函数数,微分学、积分学、矢量代数、空间解析几何无穷级数、微分方程,多元函数微分学和积分学目的:高等数学3基:1高等数学的基本知识2高度数学的基本理论3高等数学的基本计算方法提高数学素养培养:抽象思维、逻辑推理、辩证的思想方法、空间想象能力、分析问题、解决问题的能力为进一步学习打下必要的学习基础和初等数学不同,研究的不是常量而是变量,变量和变
- 《高等数学》(同济大学·第7版)第九章 多元函数微分法及其应用第四节隐函数的求导公式
没有女朋友的程序员
高等数学
以下是将含LaTeX标记的内容转为纯文本的版本:同学们好!今天我们学习《高等数学》(同济·第7版)第九章第四节隐函数的求导公式。我会用最通俗的语言和具体例子,带你彻底理解这个核心概念。如果中途有疑问,随时提出,我们一步步解决!一、隐函数是什么?为什么需要它?1.显函数vs隐函数显函数:直接写出因变量和自变量的关系,例如:y=f(x)或z=f(x,y)隐函数:因变量和自变量的关系隐含在一个方程中,例
- 高等数学》(同济大学·第7版)第七章 微分方程 第五节可降阶的高阶微分方程
没有女朋友的程序员
高等数学
好的,这是将您提供的高等数学第七章第五节教案内容中的LaTeX公式转换为纯文本格式后的版本:同学们好!今天我们学习《高等数学》第七章第五节“可降阶的高阶微分方程”。高阶微分方程(如二阶、三阶)直接求解困难,但许多方程可以通过“降阶”转化为低阶方程(如一阶方程)来求解。本节重点讲解三类可降阶的高阶微分方程,掌握它们的解法对后续学习至关重要。我会用最通俗的语言,结合大量例子,帮你彻底掌握。一、可降阶高
- 《高等数学》(同济大学·第7版)第九章 多元函数微分法及其应用第三节多元复合函数的求导法则
没有女朋友的程序员
高等数学
以下是将含LaTeX标记的内容转为纯文本的版本:同学们好!今天我们学习《高等数学》(同济·第7版)第九章第三节多元复合函数求导法则。我会用“买菜路线”和“温度变化”两个生活例子,带你彻底理解这个核心概念。如果中途有疑问,随时提出,我们一步步解决!一、从买菜路线说起:为什么需要链式法则?场景:小明从家出发,先骑车到菜市场(路程x公里),再步行到超市(路程y公里)。已知:骑车速度v_x=20km/h,
- 高等数学》(同济大学·第7版)第七章 微分方程 第三节齐次方程
没有女朋友的程序员
高等数学
同学们好!今天我们学习《高等数学》第七章第三节“齐次方程”。这是微分方程中一类重要的可转化方程,掌握它的解法对后续学习(如线性微分方程)有重要意义。我会用最通俗的语言,结合大量例子,帮你彻底掌握“齐次方程”的定义、特点和解法。一、齐次方程的定义:什么是“齐次”?1.齐次方程的两种含义在微积分中,“齐次”有两种常见含义,但这里我们特指一阶微分方程中的齐次方程:若一阶微分方程可以写成以下形式:dydx
- 【机器学习】数学基础——张量(傻瓜篇)
一叶千舟
深度学习【理论】机器学习人工智能
目录前言一、张量的定义1.标量(0维张量)2.向量(1维张量)3.矩阵(2维张量)4.高阶张量(≥3维张量)二、张量的数学表示2.1张量表示法示例三、张量的运算3.1常见张量运算四、张量在深度学习中的应用4.1PyTorch示例:张量在神经网络中的运用五、总结:张量的多维世界延伸阅读前言在机器学习、深度学习以及物理学中,张量是一个至关重要的概念。无论是在人工智能领域的神经网络中,还是在高等数学、物
- 线性代数和c语言先学哪个,线性代数和哪个更有用?
段丞博
线性代数和c语言先学哪个
一、从数学与应用数学这个专业来分析下“线性代数”和“高等数学”这两块的内容,无论哪块知识在“考研究生数学科目中的考试”都会涉汲到的,而且有些专业的考试也包括概率论与数理统计这块知识。线性代数和哪个更有用?1、线性代数内容:行列式、矩阵、向量、线性方程组、特征值和特征向量、二次型。2、高等数学内容:函数·极限·连续、导数与微分、不定积分、定积分及广义积分、中值定理的证明、常微分方程、一元微积分的应用
- ICBDDM2025:大数据与数字化管理前沿峰会
鸭鸭鸭进京赶烤
学术会议大数据图像处理计算机视觉AI编程人工智能机器人考研
在选择大学专业时,可以先从自身兴趣、能力和职业规划出发,初步确定几个感兴趣的领域。然后结合外部环境因素,如专业前景、教育资源和就业情况等,对这些专业进行深入的分析和比较。大数据专业:是一个热门且前沿的学科领域,它涉及到数据的收集、存储、处理、分析和应用等多个方面。课程设置基础课程数学基础:高等数学、线性代数、概率论与数理统计等。这些课程为大数据分析提供了必要的数学工具,例如线性代数在机器学习算法中
- 数学与加密货币:区块链技术的数学基础
AI天才研究院
计算ChatGPTAI人工智能与大数据javapythonjavascriptkotlingolang架构人工智能大厂程序员硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLM系统架构设计软件哲学Agent程序员实现财富自由
《数学与加密货币:区块链技术的数学基础》关键词数学基础加密货币区块链技术密码学分布式账本摘要本文旨在探讨数学在加密货币和区块链技术中的基础性作用。通过逐步分析,我们将深入理解数学概念如何支持加密货币的安全性、去中心化和不可篡改性。文章将涵盖初等数学和高等数学的应用,以及算法原理的讲解,帮助读者了解数学与加密货币的紧密联系。目录大纲背景介绍1.1.引言1.2.加密货币与区块链的基本概念数学基础2.1
- AI大模型从0到1记录学习 大模型技术之数学基础 day26
Gsen2819
算法人工智能大模型人工智能学习算法机器学习目标检测深度学习
高等数学导数导数的概念导数(derivative)是微积分中的一个概念。函数在某一点的导数是指这个函数在这一点附近的变化率(即函数在这一点的切线斜率)。导数的本质是通过极限的概念对函数进行局部的线性逼近。当函数f的自变量在一点x_0上产生一个增量h时,函数输出值的增量∆y与自变量增量∆x的比值在∆x趋于0时的极限如果存在,即为f在x_0处的导数,记作f’(x_0)、df/dx(x_0)或〖df/d
- 【概率论与数理统计】第二章 随机变量及其分布(1)
Arthur古德曼
概率论与数理统计概率论随机变量分布离散型连续型夏明亮
第二章随机变量及其分布第一章种学习了随机现象、随机试验、随机事件等概念,讨论了随机事件的关系、运算以及概率;且只考虑了个别事件下的频率问题。接下来,进一步第需要建立随机试验结果与实数的对应关系,这类似于函数的映射,我们称之为随机变量,以便使用高等数学的方法来研究随机试验。1离散型随机变量1.1随机变量的概念随机变量的数学定义:**定义1:**设EEE为随机试验,Ω\OmegaΩ为其样本空间,若对于
- 两矩阵相乘的秩的性质_浅析数学中的行列式与矩阵
weixin_39851977
两矩阵相乘的秩的性质利用逆矩阵解线性方程组
引言线性代数(高等代数)是进入大学之后学习代数的起点,和数学分析,解析几何并称数学三大基础课。需要注意的是,一般理工科学的是线性代数,数学系学的是高等代数,高等代数相比于线性代数,除了内容上增加了多项式以外,难度和深度也有增加。当然,高等数学和数学分析所学的内容也有所区别,这里就不再赘述。以如今的数学观点来看,线性代数几乎无处不在,它的概念与方法已经渗透到和数学相关的方方面面,这也正是为什么线性代
- 李永乐复习全书高等数学 第二章 一元函数微分学
古月忻
考研数学一高等数学刷题错题记录#考研数学一高等数学复习全书高等数学复习全书考研其他
2.1 导数与微分,导数的计算例2 设g(x)g(x)g(x)在x=0x=0x=0处存在二阶导数,且g(0)=1,g′(0)=2,g′′(0)=1g(0)=1,g'(0)=2,g''(0)=1g(0)=1,g′(0)=2,g′′(0)=1,并设f(x)={g(x)−e2xx,x≠00,x=0,f(x)=\begin{cases}\cfrac{g(x)-e^{2x}}{x},&x\ne0\\0,
- 《高等数学》(同济大学·第7版)第四章第四节有理函数的积分
没有女朋友的程序员
高等数学
一、有理函数积分的基本概念什么是有理函数?有理函数是指两个多项式相除的形式:R(x)=P(x)/Q(x)其中P(x)和Q(x)都是多项式。真分式与假分式真分式:分子次数小于分母次数例如:(x+1)/(x²+2x+3)假分式:分子次数大于等于分母次数例如:(x³+2x)/(x²+1)二、有理函数积分的解题步骤第一步:判断分式类型如果是假分式,先用多项式除法化为多项式与真分式的和。第二步:分母因式分解
- 《高等数学》(同济大学·第7版)第四章第二节换元积分法
没有女朋友的程序员
高等数学
一、换元积分法的基本思想换元积分法就像"搭积木",通过变量替换把复杂积分变成简单积分。主要有两种方法:第一类换元法(凑微分法)核心:把被积函数的一部分和dx凑成新的微分口诀:“看结构,凑微分,换变量,求积分”第二类换元法核心:直接设新的变量替换常用于含根式的积分二、第一类换元法详解我们通过具体例子来理解:例1:计算∫2x·cos(x²)dx解:观察发现x²的导数是2x,正好有2xdx设u=x²,那
- 《高等数学 第7版(同济大学 上册).pdf》资源介绍
孟津葵Gilda
《高等数学第7版(同济大学上册).pdf》资源介绍【下载地址】高等数学第7版同济大学上册.pdf资源介绍本资源提供《高等数学第7版(同济大学上册)》电子书,内容涵盖函数与极限、导数与微分、微分方程等核心章节,适合工科和理科学生系统学习。书中包含详细的理论讲解、丰富实例及习题答案,帮助读者深入理解高等数学知识。章节划分清晰,便于查找和学习。资源仅供学习研究使用,请合理利用,尊重知识产权。项目地址:h
- java实现y = x 函数的积分运算(附带源码)
Katie。
Java实战项目数学建模
1.项目背景详细介绍在高等数学中,积分是对函数进行累积求和的过程。对简单函数y=x的不定积分和定积分具有典型意义:不定积分:∫xdx=x²/2+C,其中C为常数项。定积分:∫₀ᵃxdx=a²/2。随着数值计算的广泛应用,如何在计算机程序中准确、高效地实现积分操作成为基础需求。Java作为通用语言,也需要借助数值方法或解析方法来完成函数积分。虽然y=x的积分具有解析解,但项目中往往需要处理任意函数,
- 高等数学基础(拉格朗日乘子法)
Psycho_MrZhang
人工智能数学基础数学算法
求解优化问题,拉格朗日乘子法是常用的方法之一问题引入已知目标函数f(x,y)=x2+y2f(x,y)=x^2+y^2f(x,y)=x2+y2,在约束条件xy=3xy=3xy=3下,求f(x,y)f(x,y)f(x,y)的最小值解:这是一个典型的约束优化问题,在之前最简单的办法就是通过约束条件将其中的变量进行变换,带入目标函数求出极点将y=3xy=\frac{3}{x}y=x3,带入f(x,y)=x
- 高等数学基础(牛顿/莱布尼茨公式)
Psycho_MrZhang
人工智能数学基础数学算法
牛顿/莱布尼茨公式主要是为定积分的计算提供了高效的方法,其主要含义在于求积分的函数(f(x)f(x)f(x))连续时候总是存在一条积分面积的函数(F(x)F(x)F(x))与之对应,牛顿莱布尼茨公式吧微分和积分联系了起来,提供了这种高效计算积分面积的方法参考视频理解:https://www.bilibili.com/video/BV1qo4y1G7Da/积分上限的函数及其导数设函数f(x)f(x)
- 考研数一公式笔记
代码小白 ac
人工智能
考研数学(一)核心结论与易错点详细笔记第一部分:高等数学一、函数、极限、连续(一)重要结论与公式等价无穷小替换(仅限乘除运算,极限过程为x→0或某特定值导致因子→0):sinx~xtanx~xarcsinx~xarctanx~x1-cosx~(1/2)x²e^x-1~xln(1+x)~x(1+x)^α-1~αxa^x-1~xlna(其中a>0,a≠1)重要极限:lim(sinx/x)=1(当x→0
- 先说爱的人为什么先离开
依旧天真无邪
Diary个人开发
2025年5月19日,15~23℃,贼好的一天,无事发生待办:2024年税务申报《高等数学2》取消考试资格学生名单《物理[2]》取消考试资格名单5月24日、25日监考报名《高等数学2》备课《物理[2]》备课职称申报材料教学技能大赛PPT遇见:无意间点到Google相册里面,看到好多曾经。犹记得当年谷歌相册号称无限存储空间,现在已经只有15GB了。这是我第一喜欢的女孩子,在读硕士期间,一起去过昆明失
- 26考研数学全年备考规划!!!
数学再爱我一次5555
考研学习大数据
参考书:《张宇考研数学基础30讲》、《1000题》、《张宇考研数学强化36讲》、《张宇8➕4预测卷备考工具:考研数学欧几里得小程序学习资源类全面资源覆盖:整合历年真题库、各类数学专辑和选择题库,涵盖高等数学、线性代数、概率论与数理统计等考研数学主要科目,满足用户各阶段复习需求。独家不跳步解析:每一道题目都配有详细到每一步骤的解析,确保用户完全掌握解题逻辑,能清楚了解重点题、难题的解题思路,有助于锻
- 高等数学第七章---微分方程(§7.1-§7.3微分方程概念、一阶微分方程、一阶微分线性方程)
门前云梦
高等数学考研笔记经验分享学习高等数学
§7.1微分方程有关概念例题已知曲线y=f(x)y=f(x)y=f(x)过点(1,2)(1,2)(1,2),且该曲线上任一点处的切线斜率为2x2x2x,求该曲线方程。解:由已知条件可得:曲线的导数关系:y′=2xy'=2xy′=2x(或dydx=2x\frac{dy}{dx}=2xdxdy=2x)(1)(1)(1)曲线过点(1,2)(1,2)(1,2):当x=1x=1x=1时,y=2y=2y=2(
- 硬件工程师的成长路线
可喜~可乐
嵌入式硬件硬件工程fpga开发pcb工艺物联网iot
目录第一阶段:基础知识储备第二阶段:核心技能模拟电路设计数字电路设计嵌入式系统开发系统优化和调试技巧第三阶段:专业化方向消费电子方向工业电子方向汽车电子方向第四阶段:进阶技能项目管理能力硬件可靠性设计产品认证与标准化技术文档管理团队协作与技术管理持续学习与创新第一阶段:基础知识储备在硬件工程领域,扎实的基础知识是一切深入学习的前提。数理基础不仅包括电磁学、高等数学和线性代数,还要掌握复变函数、概率
- 1.1函数、极限、连续
x峰峰
#数学考研数学极限
考研数学《函数、极限、连续》八大核心考点精讲引言函数、极限与连续是高等数学的基石,直接影响积分、微分方程等后续章节。本文从实战角度系统梳理8大核心考点,助你高效备考!考点一:函数的特性1️⃣单调性f′(x)≥0f'(x)\geq0f′(x)≥0(仅在孤点处取等号)⇒f(x)\Rightarrowf(x)⇒f(x)单调递增f′(x)≤0f'(x)\leq0f′(x)≤0(仅在孤点处取等号)⇒f(x)
- 数学:拉马努金如何想出计算圆周率的公式?
belldeep
算法科学家算法数学家
拉马努金(SrinivasaRamanujan)提出的圆周率(π)计算公式,源于他对数学模式的超凡直觉、对无穷级数和模形式的深刻洞察,以及独特的非传统数学思维方式。尽管他的思考过程带有强烈的个人色彩,甚至夹杂着神秘主义色彩,但可以从以下几个方面解析其可能的灵感来源:1.直觉与数学洞察力拉马努金自学成才,缺乏正规的高等数学训练,却对数学符号和级数有着惊人的直觉。他曾表示,许多公式是在梦中或冥想中“看
- 辞九门回忆
依旧天真无邪
Diary个人开发
2025年4月27日,13~30℃,挺好的待办:《高等数学2》期末试卷高数重修电子版材料冶金《物理》期末试卷《物理[2]》期末试卷批阅冶金《物理》作业→→统计平时成绩遇见:遇见一位小姐姐。感受或反思:不主动推动关系,是在等吗?还是在筛选?还是都不合适呢?给自己设定的期限是3个月。超过,可能就告辞啦,没有很多的时间。我会觉得可能需求不一样,没有双向奔赴的动力。而恰好双向奔赴这路才有意义。遇见:何警官
- ztree设置禁用节点
3213213333332132
JavaScriptztreejsonsetDisabledNodeAjax
ztree设置禁用节点的时候注意,当使用ajax后台请求数据,必须要设置为同步获取数据,否者会获取不到节点对象,导致设置禁用没有效果。
$(function(){
showTree();
setDisabledNode();
});
- JVM patch by Taobao
bookjovi
javaHotSpot
在网上无意中看到淘宝提交的hotspot patch,共四个,有意思,记录一下。
7050685:jsdbproc64.sh has a typo in the package name
7058036:FieldsAllocationStyle=2 does not work in 32-bit VM
7060619:C1 should respect inline and
- 将session存储到数据库中
dcj3sjt126com
sqlPHPsession
CREATE TABLE sessions (
id CHAR(32) NOT NULL,
data TEXT,
last_accessed TIMESTAMP NOT NULL,
PRIMARY KEY (id)
);
<?php
/**
* Created by PhpStorm.
* User: michaeldu
* Date
- Vector
171815164
vector
public Vector<CartProduct> delCart(Vector<CartProduct> cart, String id) {
for (int i = 0; i < cart.size(); i++) {
if (cart.get(i).getId().equals(id)) {
cart.remove(i);
- 各连接池配置参数比较
g21121
连接池
排版真心费劲,大家凑合看下吧,见谅~
Druid
DBCP
C3P0
Proxool
数据库用户名称 Username Username User
数据库密码 Password Password Password
驱动名
- [简单]mybatis insert语句添加动态字段
53873039oycg
mybatis
mysql数据库,id自增,配置如下:
<insert id="saveTestTb" useGeneratedKeys="true" keyProperty="id"
parameterType=&
- struts2拦截器配置
云端月影
struts2拦截器
struts2拦截器interceptor的三种配置方法
方法1. 普通配置法
<struts>
<package name="struts2" extends="struts-default">
&
- IE中页面不居中,火狐谷歌等正常
aijuans
IE中页面不居中
问题是首页在火狐、谷歌、所有IE中正常显示,列表页的页面在火狐谷歌中正常,在IE6、7、8中都不中,觉得可能那个地方设置的让IE系列都不认识,仔细查看后发现,列表页中没写HTML模板部分没有添加DTD定义,就是<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3
- String,int,Integer,char 几个类型常见转换
antonyup_2006
htmlsql.net
如何将字串 String 转换成整数 int?
int i = Integer.valueOf(my_str).intValue();
int i=Integer.parseInt(str);
如何将字串 String 转换成Integer ?
Integer integer=Integer.valueOf(str);
如何将整数 int 转换成字串 String ?
1.
- PL/SQL的游标类型
百合不是茶
显示游标(静态游标)隐式游标游标的更新和删除%rowtyperef游标(动态游标)
游标是oracle中的一个结果集,用于存放查询的结果;
PL/SQL中游标的声明;
1,声明游标
2,打开游标(默认是关闭的);
3,提取数据
4,关闭游标
注意的要点:游标必须声明在declare中,使用open打开游标,fetch取游标中的数据,close关闭游标
隐式游标:主要是对DML数据的操作隐
- JUnit4中@AfterClass @BeforeClass @after @before的区别对比
bijian1013
JUnit4单元测试
一.基础知识
JUnit4使用Java5中的注解(annotation),以下是JUnit4常用的几个annotation: @Before:初始化方法 对于每一个测试方法都要执行一次(注意与BeforeClass区别,后者是对于所有方法执行一次)@After:释放资源 对于每一个测试方法都要执行一次(注意与AfterClass区别,后者是对于所有方法执行一次
- 精通Oracle10编程SQL(12)开发包
bijian1013
oracle数据库plsql
/*
*开发包
*包用于逻辑组合相关的PL/SQL类型(例如TABLE类型和RECORD类型)、PL/SQL项(例如游标和游标变量)和PL/SQL子程序(例如过程和函数)
*/
--包用于逻辑组合相关的PL/SQL类型、项和子程序,它由包规范和包体两部分组成
--建立包规范:包规范实际是包与应用程序之间的接口,它用于定义包的公用组件,包括常量、变量、游标、过程和函数等
--在包规
- 【EhCache二】ehcache.xml配置详解
bit1129
ehcache.xml
在ehcache官网上找了多次,终于找到ehcache.xml配置元素和属性的含义说明文档了,这个文档包含在ehcache.xml的注释中!
ehcache.xml : http://ehcache.org/ehcache.xml
ehcache.xsd : http://ehcache.org/ehcache.xsd
ehcache配置文件的根元素是ehcahe
ehcac
- java.lang.ClassNotFoundException: org.springframework.web.context.ContextLoaderL
白糖_
javaeclipsespringtomcatWeb
今天学习spring+cxf的时候遇到一个问题:在web.xml中配置了spring的上下文监听器:
<listener>
<listener-class>org.springframework.web.context.ContextLoaderListener</listener-class>
</listener>
随后启动
- angular.element
boyitech
AngularJSAngularJS APIangular.element
angular.element
描述: 包裹着一部分DOM element或者是HTML字符串,把它作为一个jQuery元素来处理。(类似于jQuery的选择器啦) 如果jQuery被引入了,则angular.element就可以看作是jQuery选择器,选择的对象可以使用jQuery的函数;如果jQuery不可用,angular.e
- java-给定两个已排序序列,找出共同的元素。
bylijinnan
java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class CommonItemInTwoSortedArray {
/**
* 题目:给定两个已排序序列,找出共同的元素。
* 1.定义两个指针分别指向序列的开始。
* 如果指向的两个元素
- sftp 异常,有遇到的吗?求解
Chen.H
javajcraftauthjschjschexception
com.jcraft.jsch.JSchException: Auth cancel
at com.jcraft.jsch.Session.connect(Session.java:460)
at com.jcraft.jsch.Session.connect(Session.java:154)
at cn.vivame.util.ftp.SftpServerAccess.connec
- [生物智能与人工智能]神经元中的电化学结构代表什么?
comsci
人工智能
我这里做一个大胆的猜想,生物神经网络中的神经元中包含着一些化学和类似电路的结构,这些结构通常用来扮演类似我们在拓扑分析系统中的节点嵌入方程一样,使得我们的神经网络产生智能判断的能力,而这些嵌入到节点中的方程同时也扮演着"经验"的角色....
我们可以尝试一下...在某些神经
- 通过LAC和CID获取经纬度信息
dai_lm
laccid
方法1:
用浏览器打开http://www.minigps.net/cellsearch.html,然后输入lac和cid信息(mcc和mnc可以填0),如果数据正确就可以获得相应的经纬度
方法2:
发送HTTP请求到http://www.open-electronics.org/celltrack/cell.php?hex=0&lac=<lac>&cid=&
- JAVA的困难分析
datamachine
java
前段时间转了一篇SQL的文章(http://datamachine.iteye.com/blog/1971896),文章不复杂,但思想深刻,就顺便思考了一下java的不足,当砖头丢出来,希望引点和田玉。
-----------------------------------------------------------------------------------------
- 小学5年级英语单词背诵第二课
dcj3sjt126com
englishword
money 钱
paper 纸
speak 讲,说
tell 告诉
remember 记得,想起
knock 敲,击,打
question 问题
number 数字,号码
learn 学会,学习
street 街道
carry 搬运,携带
send 发送,邮寄,发射
must 必须
light 灯,光线,轻的
front
- linux下面没有tree命令
dcj3sjt126com
linux
centos p安装
yum -y install tree
mac os安装
brew install tree
首先来看tree的用法
tree 中文解释:tree
功能说明:以树状图列出目录的内容。
语 法:tree [-aACdDfFgilnNpqstux][-I <范本样式>][-P <范本样式
- Map迭代方式,Map迭代,Map循环
蕃薯耀
Map循环Map迭代Map迭代方式
Map迭代方式,Map迭代,Map循环
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年
- Spring Cache注解+Redis
hanqunfeng
spring
Spring3.1 Cache注解
依赖jar包:
<!-- redis -->
<dependency>
<groupId>org.springframework.data</groupId>
<artifactId>spring-data-redis</artifactId>
- Guava中针对集合的 filter和过滤功能
jackyrong
filter
在guava库中,自带了过滤器(filter)的功能,可以用来对collection 进行过滤,先看例子:
@Test
public void whenFilterWithIterables_thenFiltered() {
List<String> names = Lists.newArrayList("John"
- 学习编程那点事
lampcy
编程androidPHPhtml5
一年前的夏天,我还在纠结要不要改行,要不要去学php?能学到真本事吗?改行能成功吗?太多的问题,我终于不顾一切,下定决心,辞去了工作,来到传说中的帝都。老师给的乘车方式还算有效,很顺利的就到了学校,赶巧了,正好学校搬到了新校区。先安顿了下来,过了个轻松的周末,第一次到帝都,逛逛吧!
接下来的周一,是我噩梦的开始,学习内容对我这个零基础的人来说,除了勉强完成老师布置的作业外,我已经没有时间和精力去
- 架构师之流处理---------bytebuffer的mark,limit和flip
nannan408
ByteBuffer
1.前言。
如题,limit其实就是可以读取的字节长度的意思,flip是清空的意思,mark是标记的意思 。
2.例子.
例子代码:
String str = "helloWorld";
ByteBuffer buff = ByteBuffer.wrap(str.getBytes());
Sy
- org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1, column 1
Everyday都不同
$转义el表达式
最近在做Highcharts的过程中,在写js时,出现了以下异常:
严重: Servlet.service() for servlet jsp threw exception
org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1,
- 用Java实现发送邮件到163
tntxia
java实现
/*
在java版经常看到有人问如何用javamail发送邮件?如何接收邮件?如何访问多个文件夹等。问题零散,而历史的回复早已经淹没在问题的海洋之中。
本人之前所做过一个java项目,其中包含有WebMail功能,当初为用java实现而对javamail摸索了一段时间,总算有点收获。看到论坛中的经常有此方面的问题,因此把我的一些经验帖出来,希望对大家有些帮助。
此篇仅介绍用
- 探索实体类存在的真正意义
java小叶檀
POJO
一. 实体类简述
实体类其实就是俗称的POJO,这种类一般不实现特殊框架下的接口,在程序中仅作为数据容器用来持久化存储数据用的
POJO(Plain Old Java Objects)简单的Java对象
它的一般格式就是
public class A{
private String id;
public Str
![]()