笔记:动手学深度学习pytorch(机器翻译,Transformer,注意力机制和Sequence to sequence模型)
- 机器翻译
- 机器翻译与数据集
- 机器翻译
顾名思义,机器翻译就是将一段文本从一种语言翻译到另外一种语言,简称MT,而利用神经网络解决这个问题就被称为神经机器翻译(NMT)。
特征主要是输出是单词序列而不是单个单词。 输出序列的长度可能与源序列的长度不同。
- 数据预处理
将数据集清洗、转化为神经网络的输入minbatch
with open('/home/kesci/input/fraeng6506/fra.txt', 'r') as f:
raw_text = f.read()
print(raw_text[0:1000])

由于字符在计算机中是以编码的形式存在,我们通常所用的空格是 \x20 ,是在标准ASCII可见字符 0x20~0x7e 范围内。 而 \xa0 属于 latin1 (ISO/IEC_8859-1)中的扩展字符集字符,代表不间断空白符nbsp(non-breaking space),超出gbk编码范围,是需要去除的特殊字符。再数据预处理的过程中,我们首先需要对数据进行清洗。
def preprocess_raw(text):
text = text.replace('\u202f', ' ').replace('\xa0', ' ')
out = ''
for i, char in enumerate(text.lower()):
if char in (',', '!', '.') and i > 0 and text[i-1] != ' ':
out += ' '
out += char
return out
text = preprocess_raw(raw_text)
print(text[0:1000])
- 分词
字符串—单词组成的列表
num_examples = 50000
source, target = [], []
for i, line in enumerate(text.split('\n')):
if i > num_examples:
break
parts = line.split('\t')
if len(parts) >= 2:
source.append(parts[0].split(' '))
target.append(parts[1].split(' '))
source[0:3], target[0:3]
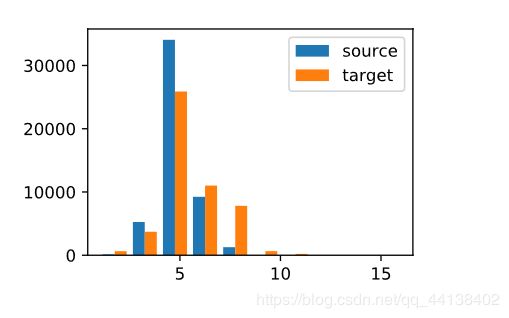
d2l.set_figsize()
d2l.plt.hist([[len(l) for l in source], [len(l) for l in target]],label=['source', 'target'])
d2l.plt.legend(loc='upper right');
- 建立词典
单词组成的列表—单词id组成的列表
def build_vocab(tokens):
tokens = [token for line in tokens for token in line]
return d2l.data.base.Vocab(tokens, min_freq=3, use_special_tokens=True)
src_vocab = build_vocab(source)
len(src_vocab)
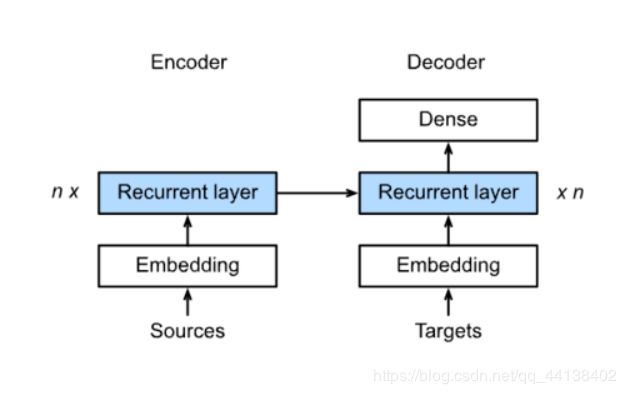
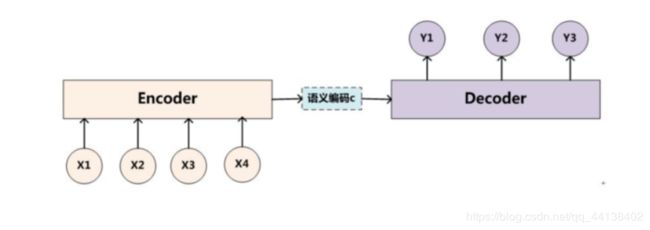
- Encoder-Decoder
encoder:输入到隐藏状态
decoder:隐藏状态到输出
class Encoder(nn.Module):
def __init__(self, **kwargs):
super(Encoder, self).__init__(**kwargs)
def forward(self, X, *args):
raise NotImplementedError
class Decoder(nn.Module):
def __init__(self, **kwargs):
super(Decoder, self).__init__(**kwargs)
def init_state(self, enc_outputs, *args):
raise NotImplementedError
def forward(self, X, state):
raise NotImplementedError
class EncoderDecoder(nn.Module):
def __init__(self, encoder, decoder, **kwargs):
super(EncoderDecoder, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
def forward(self, enc_X, dec_X, *args):
enc_outputs = self.encoder(enc_X, *args)
dec_state = self.decoder.init_state(enc_outputs, *args)
return self.decoder(dec_X, dec_state)
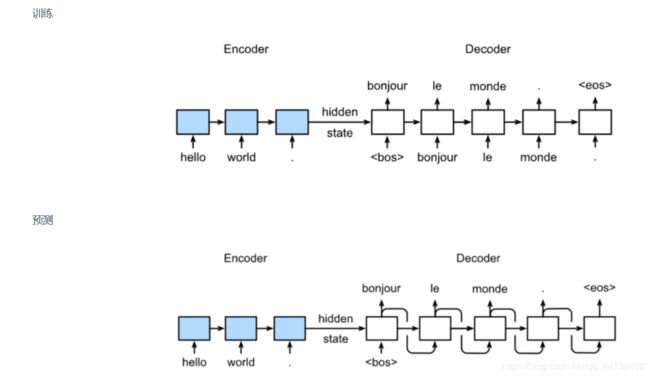
- Sequence to sequence模型
- Encoder
class Seq2SeqEncoder(d2l.Encoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqEncoder, self).__init__(**kwargs)
self.num_hiddens=num_hiddens
self.num_layers=num_layers
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.LSTM(embed_size,num_hiddens, num_layers, dropout=dropout)
def begin_state(self, batch_size, device):
return [torch.zeros(size=(self.num_layers, batch_size, self.num_hiddens), device=device),
torch.zeros(size=(self.num_layers, batch_size, self.num_hiddens), device=device)]
def forward(self, X, *args):
X = self.embedding(X)
X = X.transpose(0, 1)
out, state = self.rnn(X)
return out, state
encoder = Seq2SeqEncoder(vocab_size=10, embed_size=8,num_hiddens=16, num_layers=2)
X = torch.zeros((4, 7),dtype=torch.long)
output, state = encoder(X)
output.shape, len(state), state[0].shape, state[1].shape
![]()
- Decoder
class Seq2SeqDecoder(d2l.Decoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqDecoder, self).__init__(**kwargs)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.LSTM(embed_size,num_hiddens, num_layers, dropout=dropout)
self.dense = nn.Linear(num_hiddens,vocab_size)
def init_state(self, enc_outputs, *args):
return enc_outputs[1]
def forward(self, X, state):
X = self.embedding(X).transpose(0, 1)
out, state = self.rnn(X, state)
out = self.dense(out).transpose(0, 1)
return out, state
decoder = Seq2SeqDecoder(vocab_size=10, embed_size=8,num_hiddens=16, num_layers=2)
state = decoder.init_state(encoder(X))
out, state = decoder(X, state)
out.shape, len(state), state[0].shape, state[1].shape
![]()
- 引入注意力机制的Sequence to sequence模型
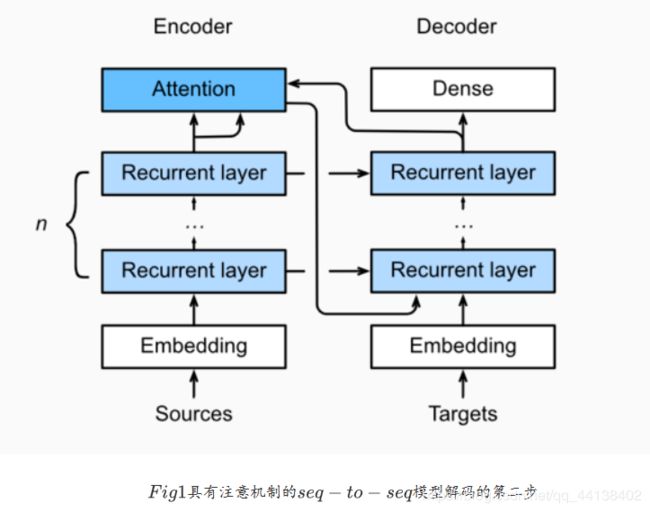
下图展示encoding 和decoding的模型结构,在时间步为t的时候。此刻attention layer保存着encodering看到的所有信息——即encoding的每一步输出。在decoding阶段,解码器的 t t t时刻的隐藏状态被当作query,encoder的每个时间步的hidden states作为key和value进行attention聚合. Attetion model的输出当作成上下文信息context vector,并与解码器输入 D t D_t Dt拼接起来一起送到解码器:

- Beam Search
简单的greedy search
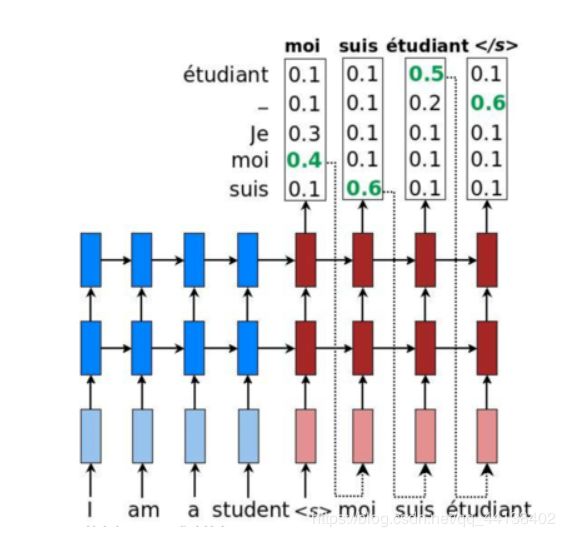
维特比算法:是一种机器学习常用的动态规划算法
维特比算法的基础可以概括为下面三点(来源于吴军:数学之美):
1、如果概率最大的路径经过篱笆网络的某点,则从开始点到该点的子路径也一定是从开始到该点路径中概率最大的。
2、假定第i时刻有k个状态,从开始到i时刻的k个状态有k条最短路径,而最终的最短路径必然经过其中的一条。
3、根据上述性质,在计算第i+1状态的最短路径时,只需要考虑从开始到当前的k个状态值的最短路径和当前状态值到第i+1状态值的最短路径即可,如求t=3时的最短路径,等于求t=2时的所有状态结点x2i的最短路径加上t=2到t=3的各节点的最短路径。
- Transformer
该模型利用attention机制实现了并行化捕捉序列依赖,并且同时处理序列的每个位置的tokens,上述优势使得Transformer模型在性能优异的同时大大减少了训练时间。
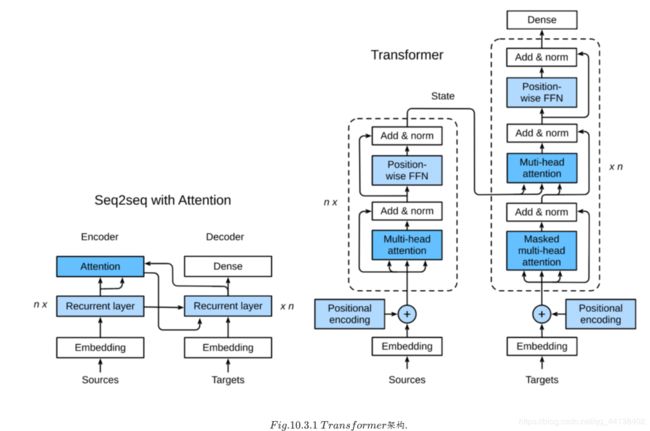
Transformer与上述Sequence to Sequence模型有三点不同之处
- Transformer blocks:将seq2seq模型重的循环网络替换为了Transformer Blocks,该模块包含一个多头注意力层(Multi-head Attention Layers)以及两个position-wise feed-forward networks(FFN)。对于解码器来说,另一个多头注意力层被用于接受编码器的隐藏状态。
- Add and norm:多头注意力层和前馈网络的输出被送到两个“add and norm”层进行处理,该层包含残差结构以及层归一化。
- Position encoding:由于自注意力层并没有区分元素的顺序,所以一个位置编码层被用于向序列元素里添加位置信息。
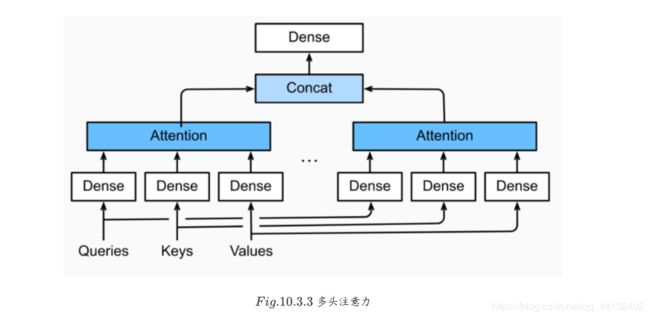
- 多头注意力层
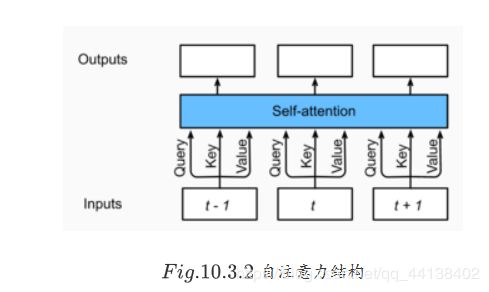
- 自注意力结构
自注意力模型是一个正规的注意力模型,序列的每一个元素对应的key,value,query是完全一致的。
多头注意力层包含 h h h个并行的自注意力层,每一个这种层被成为一个head。对每个头来说,在进行注意力计算之前,我们会将query、key和value用三个现行层进行映射,这个注意力头的输出将会被拼接之后输入最后一个线性层进行整合。
o ( i ) = a t t e n t i o n ( W q ( i ) q , W k ( i ) k , W v ( i ) v ) o^{(i)} = attention(W_q^{(i)}q, W_k^{(i)}k, W_v^{(i)}v) o(i)=attention(Wq(i)q,Wk(i)k,Wv(i)v)
我们将所有head对应的输出拼接起来,送入最后一个线性层进行整合,这个层的权重可以表示为 W o ∈ R d 0 × h p v W_o\in \mathbb{R}^{d_0 \times hp_v} Wo∈Rd0×hpv
o = W o [ o ( 1 ) , … , o ( h ) ] o = W_o[o^{(1)}, \ldots, o^{(h)}] o=Wo[o(1),…,o(h)]
接下来我们就可以实现多头注意力了
假设我们由h个头,隐藏层权重 h i d d e n _ s i z e = p q = p k = p v hidden\_size = p_q = p_k = p_v hidden_size=pq=pk=pv与query,key,value的维度一致。除此之外,因为多头注意力层保持输入与输出张量的维度不变,所以输出feature的维度也设置为 d 0 = h i d d e n _ s i z e d_0 = hidden\_size d0=hidden_size
class MultiHeadAttention(nn.Module):
def __init__(self, input_size, hidden_size, num_heads, dropout, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = DotProductAttention(dropout)
self.W_q = nn.Linear(input_size, hidden_size, bias=False)
self.W_k = nn.Linear(input_size, hidden_size, bias=False)
self.W_v = nn.Linear(input_size, hidden_size, bias=False)
self.W_o = nn.Linear(hidden_size, hidden_size, bias=False)
def forward(self, query, key, value, valid_length):
query = transpose_qkv(self.W_q(query), self.num_heads)
key = transpose_qkv(self.W_k(key), self.num_heads)
value = transpose_qkv(self.W_v(value), self.num_heads)
if valid_length is not None:
# Copy valid_length by num_heads times
device = valid_length.device
valid_length = valid_length.cpu().numpy() if valid_length.is_cuda else valid_length.numpy()
if valid_length.ndim == 1:
valid_length = torch.FloatTensor(np.tile(valid_length, self.num_heads))
else:
valid_length = torch.FloatTensor(np.tile(valid_length, (self.num_heads,1)))
valid_length = valid_length.to(device)
output = self.attention(query, key, value, valid_length)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
- 基于位置的前馈网络
Transformer 模块另一个非常重要的部分就是基于位置的前馈网络(FFN),它接受一个形状为(batch_size,seq_length, feature_size)的三维张量。Position-wise FFN由两个全连接层组成,他们作用在最后一维上。因为序列的每个位置的状态都会被单独地更新,所以我们称他为position-wise,这等效于一个1x1的卷积。
PositionWiseFFN的实现
class PositionWiseFFN(nn.Module):
def __init__(self, input_size, ffn_hidden_size, hidden_size_out, **kwargs):
super(PositionWiseFFN, self).__init__(**kwargs)
self.ffn_1 = nn.Linear(input_size, ffn_hidden_size)
self.ffn_2 = nn.Linear(ffn_hidden_size, hidden_size_out)
def forward(self, X):
return self.ffn_2(F.relu(self.ffn_1(X)))
与多头注意力层相似,FFN层同样只会对最后一维的大小进行改变;除此之外,对于两个完全相同的输入,FFN层的输出也将相等。
- Add and Norm
Transformer还有一个相加归一化层,它可以平滑地整合输入和其他层的输出,因此我们在每个多头注意力层和FFN层后面都添加一个含残差连接的Layer Norm层。
层归一化可以防止层内的数值变化过大,从而有利于加快训练速度并且提高泛化性能。
- 位置编码
与循环神经网络不同,无论是多头注意力网络还是前馈神经网络都是独立地对每个位置的元素进行更新,这种特性帮助我们实现了高效的并行,却丢失了重要的序列顺序的信息。为了更好的捕捉序列信息,Transformer模型引入了位置编码去保持输入序列元素的位置。
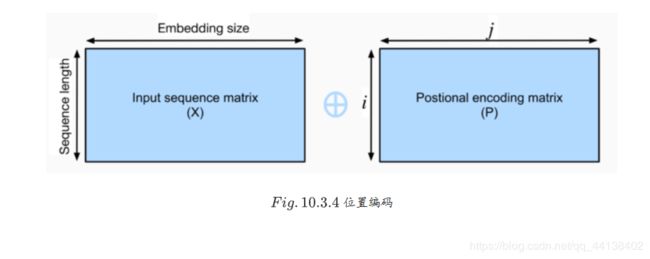
假设输入序列的嵌入表示 X ∈ R l × d X\in \mathbb{R}^{l\times d} X∈Rl×d, 序列长度 l l l为嵌入向量维度为 d d d,则其位置编码为 P ∈ R l × d P \in \mathbb{R}^{l\times d} P∈Rl×d,输出的向量就是二者相加 X + P X+P X+P。
位置编码是一个二维的矩阵,i对应着序列中的顺序,j对应其embedding vector内部的维度索引。我们可以通过以下等式计算位置编码:
P i , 2 j = s i n ( i / 1000 0 2 j / d ) P_{i,2j} = sin(i/10000^{2j/d}) Pi,2j=sin(i/100002j/d)
P i , 2 j + 1 = c o s ( i / 1000 0 2 j / d ) P_{i,2j+1} = cos(i/10000^{2j/d}) Pi,2j+1=cos(i/100002j/d)
f o r i = 0 , … , l − 1 a n d j = 0 , … , ⌊ ( d − 1 ) / 2 ⌋ for\ i=0,\ldots, l-1\ and\ j=0,\ldots,\lfloor (d-1)/2 \rfloor for i=0,…,l−1 and j=0,…,⌊(d−1)/2⌋
class PositionalEncoding(nn.Module):
def __init__(self, embedding_size, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
self.P = np.zeros((1, max_len, embedding_size))
X = np.arange(0, max_len).reshape(-1, 1) / np.power(
10000, np.arange(0, embedding_size, 2)/embedding_size)
self.P[:, :, 0::2] = np.sin(X)
self.P[:, :, 1::2] = np.cos(X)
self.P = torch.FloatTensor(self.P)
def forward(self, X):
if X.is_cuda and not self.P.is_cuda:
self.P = self.P.cuda()
X = X + self.P[:, :X.shape[1], :]
return self.dropout(X)
- 编码器
编码器包含一个多头注意力层,一个position-wise FFN,和两个 Add and Norm层。
class EncoderBlock(nn.Module):
def __init__(self, embedding_size, ffn_hidden_size, num_heads,
dropout, **kwargs):
super(EncoderBlock, self).__init__(**kwargs)
self.attention = MultiHeadAttention(embedding_size, embedding_size, num_heads, dropout)
self.addnorm_1 = AddNorm(embedding_size, dropout)
self.ffn = PositionWiseFFN(embedding_size, ffn_hidden_size, embedding_size)
self.addnorm_2 = AddNorm(embedding_size, dropout)
def forward(self, X, valid_length):
Y = self.addnorm_1(X, self.attention(X, X, X, valid_length))
return self.addnorm_2(Y, self.ffn(Y))
- 解码器
Transformer 模型的解码器与编码器结构类似,然而,除了之前介绍的几个模块之外,编码器部分有另一个子模块。该模块也是多头注意力层,接受编码器的输出作为key和value,decoder的状态作为query。与编码器部分相类似,解码器同样是使用了add and norm机制,用残差和层归一化将各个子层的输出相连。
仔细来讲,在第t个时间步,当前输入 x t x_t xt是query,那么self attention接受了第t步以及前t-1步的所有输入 x 1 , … , x t x_1,\ldots,x_t x1,…,xt。在训练时,由于第t位置的输入可以观测到全部的序列,这与预测阶段的情形项矛盾,所以我们要通过将第t个时间步所对应的可观测长度设置为t,以消除不需要看到的未来的信息。
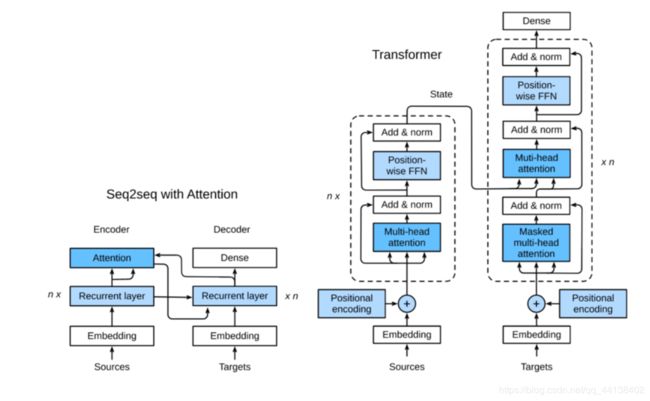
Transformer解码器除了最后一层添加一个dense layer以获得输出的置信度分数。其余和编码器一样。但是解码器还要输出编码器的输出 enc_outputs 和句子有效长度 enc_valid_length。
- 注意力机制
- 注意力机制框架
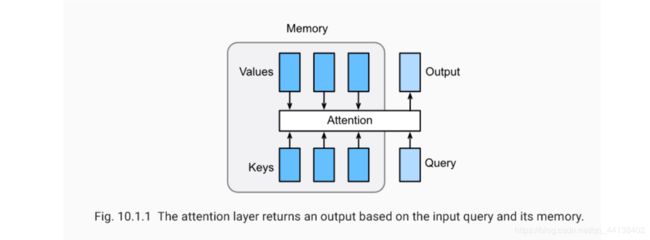
Attention 是一种通用的带权池化方法,输入由两部分构成:询问(query)和键值对(key-value pairs)。 对于一个query来说,attention layer 会与每一个key计算注意力分数并进行权重的归一化,输出的向量则是value的加权求和,而每个key计算的权重与value一一对应。
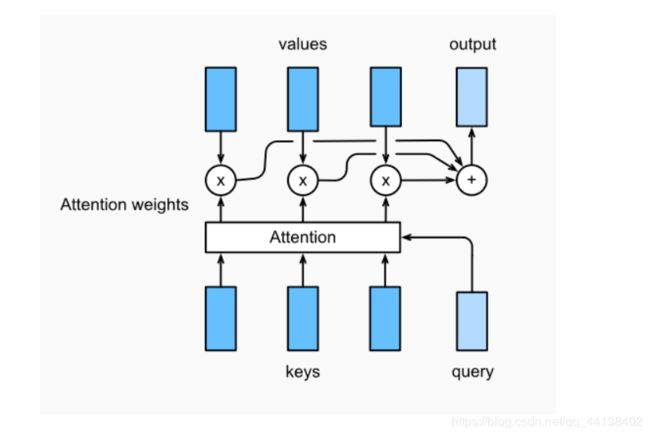
为了计算输出,我们先假设有一个函数 α \alpha α用于计算query和kry的相似性
然后计算attention scores a 1 , … , a n a_1,\ldots,a_n a1,…,an
通过这个公式 a i = α ( q , k i ) . a_i = \alpha(\mathbf q, \mathbf k_i). ai=α(q,ki).
在使用softmax函数,获得权重
b 1 , … , b n b_1,\ldots,b_n b1,…,bn = s o f t m a x ( a 1 , … , a n ) softmax(a_1,\ldots,a_n) softmax(a1,…,an)
最终的输出就是value的加权和
o = ∑ i = 1 n b i v i . \mathbf o = \sum_{i=1}^n b_i \mathbf v_i. o=∑i=1nbivi.
- softmax屏蔽
def SequenceMask(X, X_len,value=-1e6):
maxlen = X.size(1)
#print(X.size(),torch.arange((maxlen),dtype=torch.float)[None, :],'\n',X_len[:, None] )
mask = torch.arange((maxlen),dtype=torch.float)[None, :] >= X_len[:, None]
#print(mask)
X[mask]=value
return X
- 超出2维矩阵的乘法
假设 X X X和 Y Y Y是维度分别为 ( b , n , m ) (b,n,m) (b,n,m)和 ( b , m , k ) (b,m,k) (b,m,k)的张量,在经过 b b b次二维矩阵乘法后得到 Z Z Z , 维度为 ( b , n , k ) (b,n,k) (b,n,k) 。
Z [ i , : , : ] = d o t ( X [ i , : , : ] , Y [ i , : , : ] ) f o r i = 1 , … , n . Z[i,:,:] = dot(X[i,:,:], Y[i,:,:])\qquad for\ i= 1,…,n\ . Z[i,:,:]=dot(X[i,:,:],Y[i,:,:])for i=1,…,n .
torch.bmm(torch.ones((2,1,3), dtype = torch.float), torch.ones((2,3,2), dtype = torch.float))
- 多层感知机注意力
class MLPAttention(nn.Module):
def __init__(self, units,ipt_dim,dropout, **kwargs):
super(MLPAttention, self).__init__(**kwargs)
self.W_k = nn.Linear(ipt_dim, units, bias=False)
self.W_q = nn.Linear(ipt_dim, units, bias=False)
self.v = nn.Linear(units, 1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, query, key, value, valid_length):
query, key = self.W_k(query), self.W_q(key)
features = query.unsqueeze(2) + key.unsqueeze(1)
scores = self.v(features).squeeze(-1)
attention_weights = self.dropout(masked_softmax(scores, valid_length))
return torch.bmm(attention_weights, value)
总结:
- 注意力层显式地选择相关的信息。
- 注意层的内存由键-值对组成,因此它的输出接近于键类似于查询的值。