How powerful are GNN学习笔记
How powerful are GNN
1、GNN实现的功能:节点分类、连接预测、图形分类、捕获图形的相似性。
该论文有效的实现了图的分类。
2、证明了GNN在图形结构分类上能达到且最多只和 Weisfeiler-Lehman (WL) test 一样有效
WL测试:
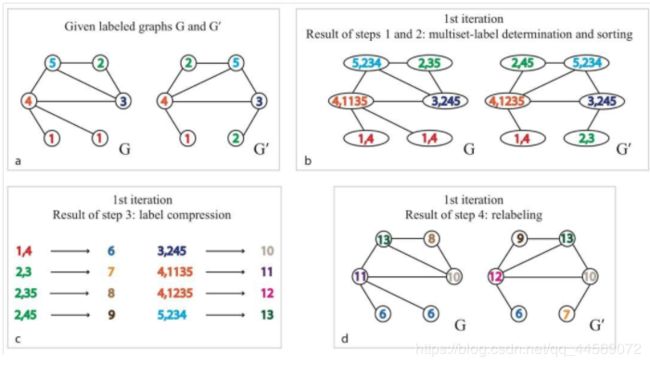


若两者的新标签不同,这表示两个图是异构的。
注:图同构问题指两个图在拓扑结构上相同
3、embedding:就是将一个节点embedding成一个特征向量;
4、参照WL test,把目前的GNN拆分为三个步骤:
Aggregate:当前节点的所有邻居如何整合
Combine:邻居和当前节点如何整合
READOUT:所有的节点如何整合
数学表示为:

通过图像具体表示为:
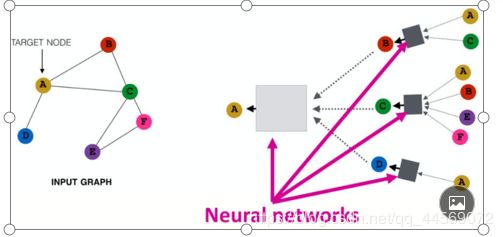
具体的聚合和拼接主要有这几种形式:
例子1:GraphSAGE:
Aggregate = weighted and ReLU + Maxpooling:
![]()
Combine = weighted and combined
![]()
例子2:GCN
the AGGREGATE and COMBINE steps are integrated:
![]()
上述两个例子求出的hv(k)可以直接用于节点分类, 若用于图形分类,还需要读出函数:
![]()
READOUT函数从最后一次迭代中聚合节点特征来获取整个图的表征向量h(G):
READOUT函数可以是一个简单的置换不变函数,例如求和或者graph-level级别的pooling函数。
“只要Aggreate/Combine/READOUT能够区别不同图的结构,那么就是和WL同等强大的。”
但是这种GNN的变体graghSage和GCN不能有效的区分图的结构:
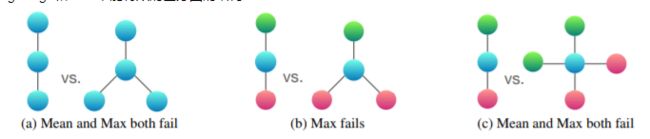
该图说明了平均池和最大池聚合器对结构对无法区分 在图3a中,每个节点具有相同的特征a,并且 f(a)在所有节点上是相同的(对于任何函数f)。当执行邻域聚合时,f(a)上的均值或最大值仍为f(a),并且通过归纳,我们总是在任何地方获得相同的节点表示。因此,均值和最大池聚合器无法捕获任何结构信息。相反,求和聚合器可以区分结构,因为2·f(a)和3·f(a)给出了不同的值。相同的参数可以应用于任何未标记的图。如果节点度不是常量值,则可以用作节点输入特征,原则上,均值可以覆盖求,但最大池不能。
图3a表明均值和最大值难以区分具有重复特征的节点的图。假设h(color)(r代表红色,g代表绿色)表示由f转换后的节点特征。图3b显示蓝色节点附近的最大值产生max(h(g),h®)和max(h(g),h®,h®),这两个值折叠成相同的表示。因此,最大池无法区分它们。相比之下,求和聚合器仍然有效,因为1/2(h(g)+h®)和1/3(h(g)+h®+h®)通常是不等同的。同样地,在图3c中,平均值和最大值均为失败1/2(h(g)+h®)和1/4(h(g)+h(g)+h®+h®)。
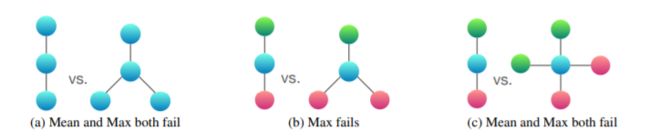
该图根据三个聚合器的表示能力对其进行排序。在这里,节点颜色表示不同的节点特征,我们假设GNN在将它们与中心节点组合之前先聚合邻居。
论文涉及的定义和理论:
定义一:多集:多重集是集合的一个广义概念,它允许其元素有多个实例。更正式地讲,多重集是一个二元组 X =(S,m),其中 S 是由其不同元素组成的 X 的基础集合,而 m:S→N (≥1) 给出了元素的多样性。直观上就是某个特定节点的邻接节点的特征向量组合。例如,{1,1,1,2,2,3}不是一个集合,而是一个多重集。
为了分析 GNN 的表达能力,我们分析了 GNN 何时将两个节点映射到嵌入空间中的相同位置。直观地说,最强大的 GNN 仅当两个节点具有相同的子树结构,并且在对应的节点上具有相同的特征时,才会将它们映射到相同的位置。(类似上面WL测试的hash过程。实际上映射过程都是单射的。)
引理2.设G1和G2为任何非同构图。如果一个图神经网络A: G → R(d) 遵循领域聚合方案,将G1和G2映射到不同的嵌入,Weisfeiler-Lehman图同构检验也判定G1和G2不是同构的。
定理二表明GNN可以达到和WL测试同样的效果。
定理 3. 设 A:G→R (d) 是一个遵循邻域聚合方案的 GNN。 通过足够的迭代,如果满足以下条件,则 A 可以将通过 Weisfeiler-Lehman 测试的图 G1 和 G2 为非同构图映射到不同的嵌入:
a) A 每次迭代聚合更新节点特征向量
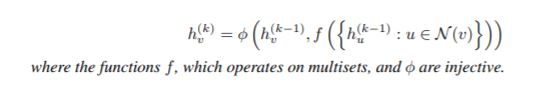
b)A 的图级别的 readout 函数,运行在节点特征的多重集上{h (k)(v)},是一个单射函数。
我们在定理3中得到的答案是肯定的:如果邻居聚合和图池化函数是单射的,那么得到的GNN就像WL测试一样强大。
在可数集上,单射性很好地描述了一个函数是否保留了输入的区别性,本文定义的所有节点特征都是可数的,那么更深层的节点是否可数?定理四表明可数性可以跨层传播。
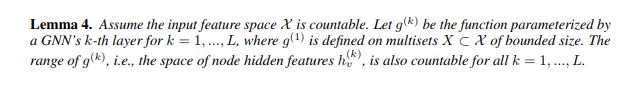
4、设计一个简单有效的区分图形结构的方法(GIN)

定理5表明求和聚合函数满足定理3中的聚合单射情况。
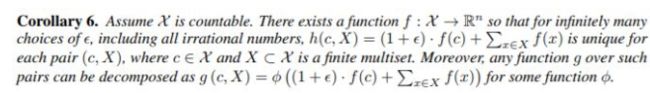
进一步的推论包括 "Aggregate设置为sum,Combine设置为1+theta都满足定理3中的单射条件。
由于通用逼近定理(Hornik等,1989; Hornik,1991),我们可以使用多层感知器(MLP)来推导和学习推论6中的f和φ,
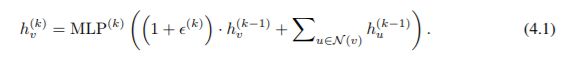
图级读出(readout)的一个重要方面是,随着迭代次数的增加,对应于子树结构的节点表征变得更加精细和全局。足够数量的迭代是实现良好区分力的关键。 然而,特征的早期迭代有时可能更好地泛化。为了考虑所有的结构信息,GIN 从模型的所有深度 / 迭代使用信息。 我们通过类似于跳跃知识网络(JK-Nets)(Xu 等人,2018)的架构来实现这一点,其中在所有的迭代中我们使用连接后的图的表征向量替换了 Eq.2.4:
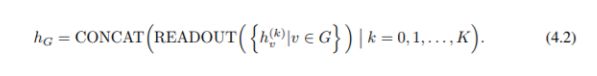
5、一些现在存在不足但值得讨论的话题:

定理7表明一层感知机结构无法区分图的结构问题。

为了描述平均聚合器可以区分多重集的类,考虑示例 X1 = (S, m) and X2 = (S, k・m),其中 X1 和 X2 具有相同的一组不同元素的集合,但 X2 包含 X1 的每个元素的 k 个副本。任何平均聚合器都将 X1 和 X2 映射到相同的嵌入,因为它只需要对单个元素的特征取平均值。因此,定理8表明平均值可以捕获多重集中元素的分布(或者比例),而不是精确的多重集。

定理9表明最大池聚合不捕获确切的结构和分布。 但是,它可能适用于某些识别任务,这些任务中识别元素或 “骨架” 更重要,而不是区分确切的结构或分布。