《大话数据结构》读书笔记--第6章 树

6.2 树的定义

1. 是n（n>=0）个结点的有限集，1.n=0为空树；2.有且仅有一个结点称为根（Root）结点;3.当n>1时，其余结点可分为m（m>0）个互不相交的有限集合，根的子树。
2. 根结点、内部结点、叶结点或终端结点
3. 树中结点的最大层次称为树的深度或高度

6.2.1 结点分类

1. 结点拥有的子树数称为结点的度
2. 度为0称为叶结点或终端结点
3. 度不为0，非终端结点或分支结点（内部结点）
4. 树的度是树内各结点点的最大值

6.2.2 结点间关系

1. 结点子树称做孩子结点，改结点称做孩子的双亲结点。
2. 兄弟结点。
3. 树中结点最大层次称为树的深度或高度
4. 森林是 m 棵互不相交的数的集合

6.3 数的抽象数据结构

6.4 树的存储结构

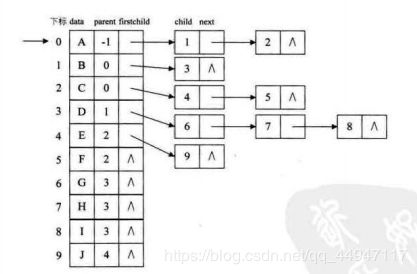
6.4.1 双亲表示法

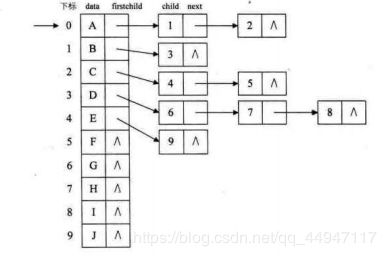
1. data（数据域） 和 parent（指针域，双亲在数组中的下标）
2. 改进：data、parent、firstchild（长子域）
3. 双亲域、长子域、右兄弟域

typedef int TElemType;
typedef struct PTNode{
   TElemeType data;  //结点数据
   int parent;       //双亲位置
}PTNode;
typedef struct{
   PTNode nodes[MAXSIZE];
   int r;     //根结点      
   int n;     //结点数
}

6.4.2 孩子表示法

1. 每个结点有多个指针域，其中每个指针指向一个子树的根节点，叫多重链表表示法。
2. 两种方式：

1.data child1 child2
指针域的个数等于树的度

2.data degree（度域） child1 child2
每个结点指针域的个数等于该结点的度，一个位置存储结点指针域的个数

6. 孩子表示法：把每个结点的孩子结点排列起来，以单链表作为存储结构，则n个结点有n个孩子链表，如果是叶子节点则此单链表为空，然后 n 个头指针又组成一个线性表，采用顺序存储结构，存放到一维数组中。
   

//孩子结点
typedef struct CTNode{
   int child;
   struct CTNode *next;
}*ChildPtr;
//表头
typedef struct {
   TElemType data;
   ChildPtr firstchild;
}CTBox;
//树结构
typedef struct{
   CTBox nodes[MAXSIZE];
   int r;     //根结点      
   int n;     //结点数;
}

7. 孩子双亲表示法
   

6.4.3 孩子兄弟表示法

1. 任意一棵树, 它的结点的第一个孩子如果存在就是唯一的，它的兄弟如果存在也是唯一的， 因此，我们设置两个指针 分别指向该结点的第一个孩子和此结点的右兄弟。

typedef struct CSNode{
    TElemType data; 
    struct CSNode *firstchild, *rightsib; 
} CSNode,*CSTree;

找双亲结点域缺陷，增加一个 parent 指针域。

6.5 二叉树

1. 二叉树是n（n>=0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

6.5.1 二叉树特点

1. 五种形态
   1.空二叉树
   2.只要一个根结点
   3.根结点只有左子树
   4.根结点只有右子树
   5.根结点既有左子树，又有右子树。

6.5.2 特殊二叉树

1. 斜树：左斜树、右斜树
2. 满二叉树：除了叶子结点（必须在同一层上），所有结点都有左右子树。
3. 完全二叉树
   

6.6 二叉树的性质

1. 在二叉树的第 i 层上至多有 2^i-1个结点
2. 深度为 k 的二叉树至多有 2^k-1 个结点
3. 对任何一棵二叉树 T，如果其终端结点数为 n₀,度为 2 的结点数为n₂,则 n₀=n₂+1
4. 具有n个结点的完全二叉树的深度为 [log₂n] + 1
5. 对于一棵有n个结点的完全二叉树的结点按层序标号，对任一结点i（i<=i<=n）有：1.如果i=1 ，则结点i是完全二叉树的根，无双亲；如果i>1，则双亲是结点[i/2]。2.如果2i>n ，则结点 i 无左孩子(结点 i 为叶子结点) ;否则其左孩子是结点2i;3.如果 2i+1>n ，则结点i无右孩子;否则其右孩子是结点 2i+1

6.7 二叉树的存储结构

1. 顺序存储结构，一般只用于完全二叉树。

6.7.2.二叉链表

1. 二叉树每个结点最多有两个孩子，数据域和两个指针域。二叉链表
2. 结构：lchild data rchild

typedef struct BiTNode{
  TElemeType data;
  struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

6.8. 遍历二叉树

1. 从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。（访问、次序）

6.8.2 二叉树遍历方法

1. 前序遍历 根 左 右
2. 中序遍历 左 根 右
3. 后序遍历 左 右 根
4. 层序遍历 一层 自上而下

     A
   B    C
  D    E  F
 G  H   I
前序：ABDGHCEIF
中序：GDHBAEICF
后序：GHDBIEFCA
层序：ABCDEFGHI

//前序 根左右
void PreOrderTraverse(BiTree T){
  if(T == null){
     return; 
  }
  printf("%c",T->data);
  PreOrderTraverse(T->lchild);
  PreOrderTraverse(T->rchild);
}
//中序 左根右
void InOrderTraverse(BiTree T){
  if(T == null){
     return; 
  }
  InOrderTraverse(T->lchild);
  printf("%c",T->data);
  InOrderTraverse(T->rchild);
}
//后序 左右根
void PostOrderTraverse(BiTree T){
  if(T == null){
     return; 
  }
  PostOrderTraverse(T->lchild);
  PostOrderTraverse(T->rchild);
  printf("%c",T->data);
}

5.已知前序和中序（后序和中序）可以确定唯一二叉树

6.9 二叉树的建立

1. 扩展二叉树
   

void CreateBiTree(BiTree *T){
   TElemType ch;
   scanf("%c",&ch);
   if(ch == "#"){
       *T  = NULL;
   }else{
     *T = (BiTree)malloc(sizeof(BiTNOde)); 
      if(!*T){
         exit(OVERFLOW);
      }else{
         (*T)->data = ch;
         CreateBiTree(&(*T)->lchild);
         CreateBiTree(&(*T)->rchild);
      }
   }
}

6.10 线索二叉树

1. 二叉树
   
2. 指向前驱和后驱的指针称为线索，加上线索的二叉链表称为线索二叉树，相应的二叉树称为线索二叉树。
3. 下图中序遍历：将 rchild 指向下一个结点。
   

所有空指针域 lchild 指向前驱。

3. 对二叉树以某种次序遍历使其变为线索二叉树的过程称做是线索化。
   
4. 区分 lchild 指向左孩子还是前驱结点，需要加 tag 判断
   
   

//二叉树的二叉线索树存储结构定义
typedef enum {
  Link,Thread
}PointerTag;//Link=0 表示指向左右孩子指针，Thread = 1 表示指向前驱或后驱
typedef struct BiThrNode{
   TElemType data;
   struct BiThreNode *lchild,*rchild;
   PointerTag LTag;
   PointerTag RTag;
}BiTheNode,*BiTheTree;

5. 线索化实质，将二叉链表中的空指针改为指向前驱或后驱的线索，线索化的过程就是在遍历的过程中修改空指针的过程。

BiThrThree pre;
void InTheading(BiThrThree p){
  if(p){
    InThreadDing(p->lchild);//递归左子树线索化
    if(!p->lchild){      //没有左孩子
      p->LTag = Thread;  //前驱线索
      p->lchild = pre;   //指向前驱
    }
     if(!pre->rchild){  //前驱没有右孩子
      pre->RTag = Thread; 
      pre->rchild = p;   //前驱右孩子指针指向后驱（当前节点 p）
    }
    pre = p; // 保持 pre 指向 p 的前驱
    InThreading(p->rchild); //递归右子树线索化
  }
}

//遍历
Status InOrderTraverse_Thr(BiThrTree T){
    BiThrTree p;
    p = T->lchild; //p 指向根节点
    while(p != T){ //空树或遍历结束，p == T
      while(p->LTag == Link){ //LTag ==0是循环中序序列第一个结点
        p = p->lchild;
        printf("%c",p->data);//显示结点数据
        while(p->RTag == Thread && p->rchild !=T){
           p = p->rchild;
           printf("%c",p->data);
      }
      p = p->rchild; //p进至其右子树根
    }
    return OK;
}

1. 如果所用的二叉树需经常遍历或查找结点时需要某种遍历序列中的前驱和后继，那么采用线索二叉链袤的存储结构就是非常不错的选择。

6.11 树、森林与二叉树的转换

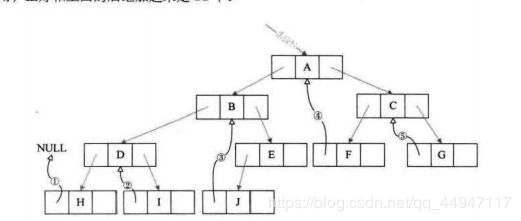
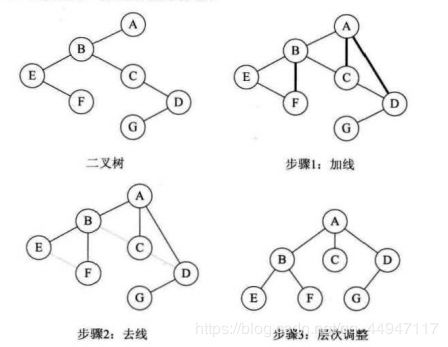
6.11.1 树转换为二叉树

1. 加线，兄弟结点加线
2. 去线，保留第一个孩子线
3. 层次调整，顺时针选择一定角度

6.11.2 森林转换为二叉树

1. 把每棵树转换成二叉树
2. 第一棵不动，后面的树把根极点作为前一棵根结点孩子。

6.11.3 二叉树转换为树

6.11.4 二叉树转换为森林

6.11.5 树与森林的遍历

1. 树遍历：先根遍历、后根遍历
2. 森林遍历：前序、后序

6.12 赫夫曼树及应用

6.12.1 赫夫曼树

1. 从树中一个结点到另一个结点之间的分支构成两个结点之间的路，路径上的分支数目称做路劲长度。
2. 树的路径长度就是从树根到每一结点的路径长度之和
3. 带权路径长度 WPL 最小的二叉树称做赫夫曼树，也叫最优二叉树。

6.12.3 赫夫曼编码

1. 若要设计长短不等的编码，则必须是任一字符的编码都不是另一个字符的编码的前缀，这种编码称做前缀编码。