[TOC]
写在前面
本篇文章整理《数据结构(C++语言版)》关于二叉树这种线性结构知识点。
整个数据结构部分章节列表如下:
1 向量
2 列表
3 栈
4 队列
5 二叉树
6 图
6 图
6.1 图的描述
比较特殊的两种图
(1)欧拉环路:经过所有的边有且仅有一次的环路。
(2)哈密尔顿环路经过所有点有且仅有一次的环路。
邻接矩阵与关联矩阵
图可以通过矩阵形式进行描述。
(1)邻接矩阵:描述顶点之间相互邻接关系。(n x n格式,n个顶点)
(2)关联矩阵:描述顶点与边之间的关联关系。(n x e格式,n个顶点,e条边)
6.2 图结构的实现
图结构接口定义代码如下
template
class Graph {
private:
void reset() { //所有顶点,边的辅助信息复位
for (int i = 0; i < n; i++) { //顶点
status(i) = UNDISCOVERED; dTime(i) = fTime(i) = -1;
parent(i) = -1; priority(i) = INT_MAX;
for (int j = 0; j < n; j++) //边
if (exists(i, j)) status(i, j) = UNDETERMINED;
}
}
public: /*...顶点操作、边操作,图算法
}
6.2.1 顶点类型的实现
代码如下
typedef enum { UNDISCOVERED, DISCOVERED, VISITED } VStatus;
template
struct Vertex { //顶点对象(并未严格封装)
Tv data; int inDegree, outDegree; //数据、出入度
VStatus status; //(如上三种)状态
int dTime, fTime; //时间标签
int parent; //在遍历树中的父节点
int priority; //在遍历树中的优先级(最短通路,极短跨边等)
Vertex(Tv const & d): //构造函数,初始化列表,构造新顶点
data(d), inDegree(0), outDegree(0), status(UNDISCOVERED),
dTime(-1), fTime(-1), parent(-1), priority(INT_MAX) {}
}
TIPS:关于typedef与define
1.使用方式
宏定义: #difine int_PTR int * //将int * 用int_PTR代替
typedef: typedef int * int_ptr //将int * 用int_ptr代替
2.编译处理
宏定义是预处理指令,在编译预处理时进行简单的替换,不做正确性检查;typedef是在编译时处理的。
const int_ptr p; //相当于const int * p,把指针锁住,即p不能改变,但其指向的内容可变
const int_PTR p; //仅仅将其替换掉,相当于const( int * p),把指针指向对象锁住,即p指向的内容不能改变
6.2.2 边类型的实现
代码如下
typedef enum{UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD} EStatus;
template
struct Edge { //边对象(并未严格封装)
Te data; //数据
int weight; //权重
EStatus status; //类型
Edge(Te const& d, int w) : //构造函数,初始化列表,构造新边
data(d), weigth(w), status(UNDETERMINED) {}
}
6.2.3 基于邻接矩阵实现图结构
首先将顶点集与边集兑现为对应的数据结构。
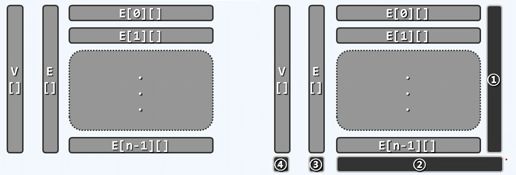
对于边集而言,这里套用了两层Vector结构,继承了Vector中重载的[ ]操作符用法。第一层,将以某个顶点为中心的所有关联边整合(行向量),随后再整合为列向量。因而E[i] [j]即为邻接矩阵。
代码如下
template
class GraphMatrix : public Graph {
private:
Vector< Vertex > V; //顶点集
Vector< Vector< Edge* > > E; //边集
public:
/*...操作接口...*/
GraphMatrix() {n = e = 0; }
~GraphMatrix() { //析构
for (int j=0; j 6.3 相关算法
6.3.1 顶点操作
1.枚举当前顶点所有邻接顶点
即从当前顶点i开始,依次判断其余顶点j与顶点i之间是否有关联边(i, j)存在。
int nextNbr(int i, int j) { //若已枚举至邻居j,则转向下一个邻居
while( (-1 < j) && !exits(i, --j) ); //逆序查找
return j;
}
int firstNbr(int i){
return nextNbr(i, n);
}
2.顶点插入
插入一个新顶点,需要对邻接矩阵进行扩充。①表示增加每个顶点到新顶点的边集合(初始化为NULL)②表示新顶点到每个顶点的边集合(初始化为NULL)③④表示对边集合与顶点集合扩充。
int insert(Tv const & vertex){ //插入顶点,返回编号
for(int j = 0; j < n; j++) E[j].insert(NULL); //①
n++; //增大矩阵列数
E.insert( Vector< Edge* >(n, n, NULL) ); //②③
return V.insert( Vertex (vertex) ); //④
}
3.顶点删除
Tv remove(int i) { //删除顶点及其关联边,返回该顶点信息
for(int j = 0; j < n; j++) {//删除关联矩阵中第i行(删除所有出边)
if (exists(i, j)) {
delete E[i][j];
V[j].inDegree--;
}
}
E.remove(i); //删除第i行
for(int j = 0; j < n; j++) {//删除关联矩阵第i列(删除所有入边)
if (exists(j, i)) {
delete E[j][i];
V[j].outDegree--;
}
}
Tv vBak = vertex(i); //备份顶点i的信息
V.remove(i);
return vBak;
}
6.3.2 广度优先遍历
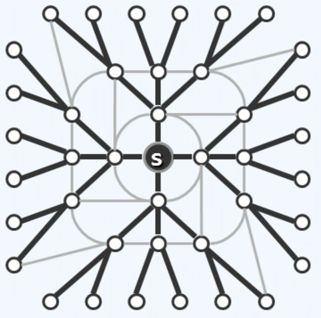
以当前顶点为中心,遍历其所有邻接点。再以每个邻接点为中心,遍历其所有尚未访问的邻接点。该算法的实现与树的层次遍历类似,或者说,树的层次遍历是图的广度优先遍历的一种特殊情况。
具体算法中,每个顶点共设置三种状态{UNDISCOVERED, DISCOVERED, VISITED}分别表示未被发现、被发现、被访问,每条边共设置三种状态{UNDETERMINED, CROSS, TREE}分别表示未被发现、被访问、不访问。
template
void Graph::BFS(int v, int & clock){
Queue Q; status(v) = DISCOVERED; Q.enqueue(v);
while( !Q.empty() ) {
int v = Q.dequeue();
dTime(v) = ++clock; //取出队首顶点v
for(int u = firstNbr(v); -1 < u; u = nextNbr(v, u)) { //找寻当前顶点v的邻接点u
if(UNDISCOVERED == status(u)) { //若u未被发现
status(u) = DISCOVERED; Q.enqueue(u); //发现该节点并入队
status(v, u) = TREE; parent(u) =v; //访问该关联边
} else //若u已被发现(已入队)或已被访问
status(v, u) = CROSS; //设置该关联边为不访问状态
}
status(v) = VISITED;
}
}
变式:若该图中包含不只一个连通域的情形,采用BFS搜索,只需逐一检查每个顶点,若状态为UNDISCOVERED,则对当前顶点启动BFS搜索。
6.3.3 深度优先遍历
起始于顶点s,在其未被访问的邻接点中任选其一,递归执行。
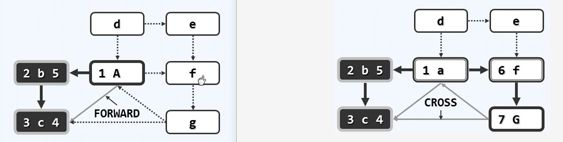
设父节点为v,其递归执行的子节点u。
①若u的邻接节点s状态为UNDISCOVERED,则继续递归执行;
j的邻居包含g么?????????
②若状态为DISCOVERED(表明该节点s已置入遍历树中),则将边(u,s)设置为BACKWARD(该边不置入遍历树),回退到其父节点u;
③若状态为VISITED,则比较节点u与节点s的发现时间(dTime)标签。若u标签更小,即u更早被发现,则标记边(u,s)为FORWARD;否则,标记为CROSS。
代码如下
template
void Graph::DFS(int v, int & clock) {
dTime(v) = ++clock; status(v) = DISCOVERED;
for(int u = firstNbr(v); -1 < u; u = nextNbr(v, u)) {
switch( status(u) ) {
case UNDISCOVERED: //u尚未发现,支撑数可在u点进行拓展
status(v, u) = TREE; parent(u) =v; DFS(u, clock); break; //在u点递归
case DISCOVERED: //u已被发现
status(v, u) = BACKWARD; break;
default: //u已访问完毕
status(v, u) = dTime(v) < dTime(u) ? FORWARD : CROSS; break;
}
status(v) = VISITED; fTime(v) = ++clock; //记录节点访问完毕的时钟
}
嵌套引理
1.顶点活动期active[u] = ( dTime[u], fTime[u] )
2.给定有向图G=(V, E)及其任一DFS森林,则
active[u] ⊆ active[v],则u是v的后代;
active[u] ⊇ active[v],则u是v的祖先;
active[u] ∩ active[v] = ∅,则u与v无亲缘关系。