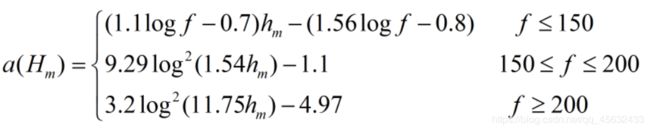无线信道模型
目录
- 1 信道 无线信道
- 天线增益
- 2 信道模型
- 2-1 瑞利衰落信道模型
- 2-2 莱斯衰落信道模型
- 2-3 AWGN信道模型
- 2-4 适用条件对比
- 3 无线信道中的衰落
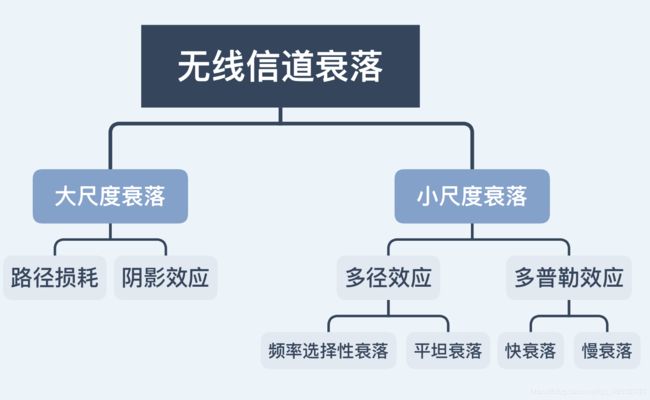
- 3-1 大尺度衰落与小尺度衰落
- 3-2 路径损耗
- 3-3 多径传播
- 3-4 四种小尺度衰落
- 3-5 阴影效应
- 4 Hata模型
- 4-1 简介
- 4-2 适用条件
- 4-3 传播损耗公式及其单位
- 5 参考文章
1 信道 无线信道
各类信号从发射端发送出去以后,在到达接收端之前经历的所有路径统称为信道。
如果其中传输的是无线电信号,电磁波所经历的路径称之为无线信道。
天线增益
在位置A处可以达到相同的辐射强度
- 方向性天线,A 在其最大辐射方向上,发射功率为 P t P_t Pt
- 理想化点源的发射功率为 P t G P_tG PtG
则G为该方向性天线的增益,理想化点源 G = 1 G=1 G=1,方向性天线 G > 1 G>1 G>1
2 信道模型
信道模型是用数学表达式描述信道特性
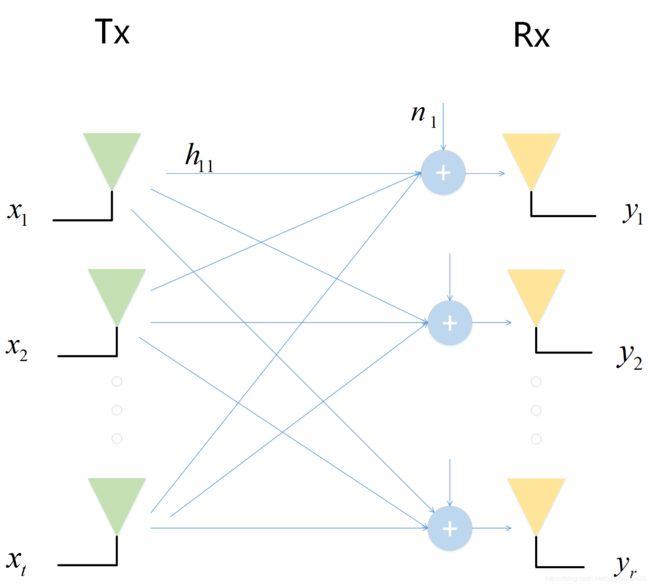
h i j h_{ij} hij,其中 i i i表示接受天线, j j j表示发送天线, H 21 H_{21} H21表示 1 1 1发 2 2 2收
y 1 = h 11 x 1 + h 12 x 2 + . . . + h 1 t x t y_1=h_{11}x_1+h_{12}x_2+...+h_{1t}x_t y1=h11x1+h12x2+...+h1txt
y 2 = h 21 x 1 + h 22 x 2 + . . . + h 2 t x t y_2=h_{21}x_1+h_{22}x_2+...+h_{2t}x_t y2=h21x1+h22x2+...+h2txt
. . . ... ...
y r = h r 1 x 1 + h r 2 x 2 + . . . + h t x t y_r=h_{r1}x_1+h_{r2}x_2+...+h_{t}x_t yr=hr1x1+hr2x2+...+htxt
写成矩阵形式为:
y = H x + n \mathbf{y=Hx+n} y=Hx+n
[ y 1 y 2 . . . y r ] = [ h 11 h 12 . . . . . . h 1 t h 21 h 22 . . . . . . h 2 t . . . . . . . . . . . . . . . h r 1 h r 2 . . . . . . h r t ] [ x 1 x 2 . . . x t ] + [ n 1 n 2 . . . n r ] \begin{bmatrix} y_1\\y_2\\...\\y_r\end{bmatrix} = \begin{bmatrix} h_{11}&h_{12}&...&...&h_{1t}\\ h_{21}&h_{22}&...&...&h_{2t}\\ ...&...&...&...&...\\ h_{r1}&h_{r2}&...&...&h_{rt}\\ \end{bmatrix} \begin{bmatrix} x_1\\x_2\\...\\x_t\end{bmatrix} +\begin{bmatrix} n_1\\n_2\\...\\n_r\end{bmatrix} ⎣⎢⎢⎡y1y2...yr⎦⎥⎥⎤=⎣⎢⎢⎡h11h21...hr1h12h22...hr2........................h1th2t...hrt⎦⎥⎥⎤⎣⎢⎢⎡x1x2...xt⎦⎥⎥⎤+⎣⎢⎢⎡n1n2...nr⎦⎥⎥⎤
2-1 瑞利衰落信道模型
信号通过无线信道之后,其信号的幅度是随机的,即“衰落”,并且其包络服从瑞利分布,这样的信道叫做“瑞利信道”。
瑞利衰落属于小尺度的衰落效应,它总是叠加于如阴影、衰减等大尺度衰落效应上。
2-2 莱斯衰落信道模型
如果收到的信号中除了经反射折射散射等来的信号外, 还有从发射机直接到达接收机 (如从卫星直接到达地面接收机)的信号,那么总信号的强度服从莱斯分布, 故称为莱斯衰落。
信号在传输过程中由于多径效应,接收信号是直射信号(主信号)和多径信号的叠加,此时接收信号的包络服从莱斯分布。
2-3 AWGN信道模型
信道的噪声在频谱(频域)上均匀分布(即白噪声),幅度上(时域)呈高斯分布
噪声在整个信道带宽下功率谱密度为常数
2-4 适用条件对比
| 信道模型 | 适用条件 | 适用场景 |
|---|---|---|
| 瑞利信道 | 从发射机到接收机不存在直射信号的情况,即经过发射、折射或者衍射到达接收机 | 存在能够大量散射无线电信号的障碍物的无线传播环境:多径通道和多普勒频移现象、电离层和对流层发射的短波信道,以及建筑物密集的城市环境 |
| 莱斯信道 | 移动台与基站间存在直射波信号,即有一条主路径 | |
| AWGN信道 | 不存在干扰,网络中只有一个基站,基站下只有一个终端 | 恒参信道,例如卫星通信,光纤信道,同轴电缆 香农公式成立条件 |
3 无线信道中的衰落
自由空间传播模型:
L 0 = 32.45 + 20 l o g ( f ) + 20 l o g ( d ) L_0=32.45+20log(f)+20log(d) L0=32.45+20log(f)+20log(d)
3-1 大尺度衰落与小尺度衰落
大尺度是指距离远远大于波长,是宏观意义上的衰落;小尺度是几倍波长,短距离、短时间,研究的是微观意义上的衰落。
大尺度衰落:信号经过长距离(几百米到几十公里)传播后场强的变化,大尺度衰落主要是由于建筑物、高山等的阻挡造成的,因此也叫作阴影衰落。
小尺度衰落:在电波传播过程中,信号场强在短距(几个信号波长)或短时(秒级)上呈现出快速波动的状况,包括由移动台和基站的相对运动造成多普勒频移引起的时间选择性衰落和由多径引起的频率选择性衰落。
3-2 路径损耗
路径损耗,或称传播损耗,指电波在空间传播所产生的损耗,是由发射功率的辐射扩散及信道的传播特性造成的,反映宏观范围内接收信号功率均值的变化。
大尺度路径损耗:大尺度平均路径损耗用于测量发射机和接收机之间信号的平均衰落,定义为有效发射功率和平均接收功率之间的差值。几种常用的描述大尺度衰落的模型有自由空间模型、布灵顿模型、EgLi模型、Hata-Okumura模型。
路径损耗模型
实测表明,在发射功率、天线参数和高度、电波频率给定的情况下,平均路径损耗 P L PL PL随传播距离(T-R距离) d d d的变化规律为:
P L ( d ) ∝ ( d d 0 ) n , d > d 0 PL(d)\propto(\frac{d}{d_0})^n ,d>d_0 PL(d)∝(d0d)n,d>d0
其中 d 0 d_0 d0为靠近发端的参考点距发端的距离。该参考点处的路径损耗一般可以通过实测获得, n n n为路径损耗指数,具体指数依赖于传播环境。
对数距离路径损耗模型
距离增加 10 10 10,分贝值增加 10 n d B 10ndB 10ndB
P L ( d a ) − P L ( d b ) = 10 n d B PL(d_a)-PL(d_b)=10ndB PL(da)−PL(db)=10ndB
d a = 10 d b d_a=10d_b da=10db
P L ( d ) [ d B ] = P L ( d 0 ) [ d B ] + 10 n l g ( d d 0 ) PL(d)[dB]=PL(d_0)[dB]+10nlg(\frac{d}{d_0}) PL(d)[dB]=PL(d0)[dB]+10nlg(d0d)
P r [ d B m ] = P t [ d B m ] − P L ( d 0 ) [ d B ] − 10 n l g ( d d 0 ) , d > d 0 Pr[dBm]=P_t[dBm]-PL(d_0)[dB]-10nlg(\frac{d}{d_0}),d>d_0 Pr[dBm]=Pt[dBm]−PL(d0)[dB]−10nlg(d0d),d>d0
3-3 多径传播
多径传播:从发射机天线发射的无线电波(信号),沿两个或多个路径到达接收机天线的传播现象。
多径效应:指电磁波经不同路径传播后,各分量场到达接收端时间不同,按各自相位相互叠加而造成干扰,使得原来的信号失真,或者产生错误。瑞利衰落
3-4 四种小尺度衰落
多普勒扩展1与相干时间2表征了信道时变特性,时延扩展和相干带宽用于描述本地信道时间色散特性。多普勒扩展与相干时间成反比,时延扩展与相干带宽3成反比。
频率选择性衰落:
- 信号带宽>信道带宽
- 时延扩展>发射信号符号周期
平坦衰落:
- 信号带宽<信道带宽
- 时延扩展<发射信号符号周期
快衰落:
- 高多普勒扩展
- 相干时间<发射信号符号周期
- 信道变化快于基带信号变化
慢衰落:
- 低多普勒扩展(与基带信号带宽相比很小)
- 相干时间>发射信号符号周期
- 信道变化慢于基带信号变化
3-5 阴影效应
在无线通信系统中,移动台在运动的情况下,由于大型建筑物和其他物体对电波的传输路径的阻挡而在传播接收区域上形成半盲区,从而形成电磁场阴影,这种随移动台位置的不断变化而引起的接收点场强中值的起伏变化叫做阴影效应。
阴影衰落一般服从对数正态分布
在给定距离处,实际的路径损耗呈现出随机变化,其分贝值(dB)的概率密度函数为:
p ( P L ) = 1 2 π σ P L e x p ( − ( P L − μ P L ) 2 2 σ P L 2 ) p(PL)=\frac{1}{\sqrt{2\pi}\sigma_{PL}}exp(-\frac{(PL-\mu_{PL})^2}{2\sigma^2_{PL}}) p(PL)=2πσPL1exp(−2σPL2(PL−μPL)2)
其中 μ P L \mu_{PL} μPL为对数距离路径损耗模型中所得到的给定距离处的平均路径损耗的分贝值
对数正态阴影模型的另一种形式:
P L ( d ) [ d B ] = P L ( d 0 ) [ d B ] + 10 n l g ( d d 0 ) + X σ [ d B ] PL(d)[dB]=PL(d_0)[dB]+10nlg(\frac{d}{d_0})+X_{\sigma}[dB] PL(d)[dB]=PL(d0)[dB]+10nlg(d0d)+Xσ[dB]
其中 X σ X_{\sigma} Xσ为均值为 0 d B 0dB 0dB,标准差为 σ P L ( d B ) \sigma_{PL}(dB) σPL(dB)的正态随机变量。
4 Hata模型
4-1 简介
以准平坦地形大城市地区的场强中值路径损耗作为基准,对不同的传播环境和地形条件等因素用校正因子加以修正。
4-2 适用条件
三点假设:
● 作为两个全向天线之间的传播损耗处理;
● 作为准平滑地形而不是不规则地形处理;
● 以城市市区的传播损耗公式作为标准,其他地区采用校正公式进行修正
| 参数描述 | 参数值 |
|---|---|
| 无线电载波频率f | 150 M H z − 1500 M H z 150MHz-1500MHz 150MHz−1500MHz |
| 基站天线垂直高度 H b H_b Hb | 30 m − 200 m 30m-200m 30m−200m |
| 移动台天线垂直高度 H m H_m Hm | 1 m − 10 m 1m-10m 1m−10m |
| 移动台与基站间的传播距离 d d d | 1 k m − 20 k m 1km-20km 1km−20km |
4-3 传播损耗公式及其单位
P L = 69.5 + 29.16 l o g ( f ) − 13.8 l o g H b − a ( H m ) + [ 44.9 − 6.5 l o g H b ] l o g d − K PL=69.5+29.16log(f)-13.8logH_b-a(H_m)+[44.9-6.5logH_b]logd-K PL=69.5+29.16log(f)−13.8logHb−a(Hm)+[44.9−6.5logHb]logd−K
a ( H m ) a(H_m) a(Hm)与 K K K的取值4:
| a ( H m ) a(H_m) a(Hm) | K K K | |
|---|---|---|
| 大城市 | 3.2 l o g 2 ( 11.75 H m ) − 4.97 3.2log^2(11.75H_m)-4.97 3.2log2(11.75Hm)−4.97 | 0 0 0 |
| 中小城市 | ( 1.11 l o g f − 0.7 ) H m − ( 1.56 l o g f − 0.8 ) (1.11logf-0.7)H_m-(1.56logf-0.8) (1.11logf−0.7)Hm−(1.56logf−0.8) | 0 0 0 |
| 郊区 | ( 1.11 l o g f − 0.7 ) H m − ( 1.56 l o g f − 0.8 ) (1.11logf-0.7)H_m-(1.56logf-0.8) (1.11logf−0.7)Hm−(1.56logf−0.8) | 2 l o g 2 ( f / 28 ) + 5.4 2log^2(f/28)+5.4 2log2(f/28)+5.4 |
| 乡镇 | ( 1.11 l o g f − 0.7 ) H m − ( 1.56 l o g f − 0.8 ) (1.11logf-0.7)H_m-(1.56logf-0.8) (1.11logf−0.7)Hm−(1.56logf−0.8) | 4.78 l o g 2 f − 18.33 l o g f + 40 4.78log^2f-18.33logf+40 4.78log2f−18.33logf+40 |
当 H m = 1.5 H_m=1.5 Hm=1.5时, a ( H m ) = 0 a(H_m)=0 a(Hm)=0
| 物理量 | 单位 |
|---|---|
| 载波频率 f f f | MHz |
| 基站天线垂直高度 H b H_b Hb | m m m |
| 移动台天线垂直高度 H m H_m Hm | m m m |
| 移动台与基站间的传播距离 d d d | k m km km |
| 移动台天线的校正因子 a ( H m ) a(H_m) a(Hm) | d B dB dB |
| 传播损耗 P L PL PL | d B dB dB |
5 参考文章
【LTE基础知识】无线传播模型之Okumura-Hata模型介绍
无线通信中的小尺度衰落
无线信道衰落分类
无线信道信道衰落知识点总结
瑞利、莱斯与Nakagami-m信道衰落模型
通信 之 无线信道衰落
无线通信中信号的多径效应
西电复试——无线通信05级课本第4章节 .ppt
大尺度路径损耗(第4章) 移动无线信道课件