算法入门之递归

递归

在正式介绍递归之前，我们首先要先来了解以下递归的定义是什么。

其实，递归就是反复的调用自身的函数，以此达到将问题规模一步步缩小的结果。

好了，下面开始说人话。还是用一个引例来进入今天的主题。

引例

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自上而下、由小到大按顺序放置n个金盘。
游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。
操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上。

分析

为了更好的理解递归，我们先从最简单的开始：

假设n=1，那么移动方法就很简单了，直接进行移动就可：

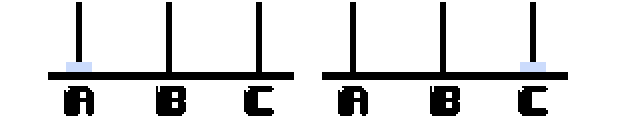
那么我们再来看一下n=2的情况：

这里我们就要借助B柱来完成这个任务，可以先将蓝色的移动到B柱上，然后进行移动即可：

下面我们再来看一下n=3时的移动方法。在这里，我们需要用到一点上一步的方法。

我们将三个圆盘从小到大编号为1、2、3。那么我们可以先将1、2盘移动到B上（可以参考上面n=2时的情况）然后再将然后将3移动到C上，最后再将1、2从B移动到C上。

具体步骤为：
1）1、2（A->B）
2）3（A->C）
3）1、2（B->C）

那么我们很容易就能找到解决方案，步骤如下示意图所示：

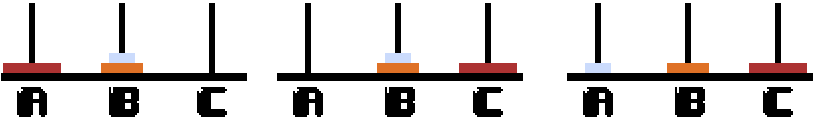
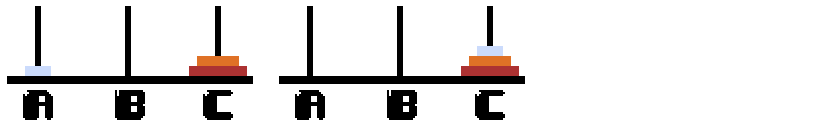
看了n=3时的思路，那么我们再来看一下n=4时的方法，与n=3时类似。从小到大编号为1、2、3、4。

具体步骤为：
1）1、2、3（A->B）
2）4（A->C）
3）1、2、3（B->C）

而上面的步骤一和三可以使用刚刚n=3时的移动方法。

通过上面的讨论，我们可以看出：每次我们都将问题规模缩小简化，最终达到了我们能够实现的目标，那么我们现在来讨论一下当圆盘数为n时的情况：

很容易写出步骤为：
1）1、2、……、n-1（A->B）
2）n（A->C）
3）1、2、……、n-1（B->C）

上面的步骤一和三又可以参考n-1时的移动情况。

找到了递归的式子。下面我们还有一个很重要的任务：找到递归边界。

递归边界就是递归停下来的条件，否则将会不断调用函数无法跳出。

我们可以看出，汉诺塔问题每次都将n的规模不断减小，每次调用函数时n的数值也在不断变小，那么我们是不是可以设置一个n的最小值来达到设定一个递归边界的目的呢？

不难看出，n为1时就是函数调用的边界，只需要将圆盘从A移动到C即可。n不可能是正整数以外的数。

代码

我们来看一下如何写出代码来实现汉诺塔游戏：

首先，我们先写一个圆盘移动的函数，避免代码过分赘余。

void move(char x, char y)
{
	printf("%c -> %c\n", x, y);
}

那么我们就开始写主要的递归函数void hanoi(int n, char a, char b, char c)了：

首先，我们要在函数内部加一个判断条件，即刚刚我们所说的递归边界，让n等于1时直接将圆盘进行移动，不再调用自身的函数。

if(n==1)
	move(a, c);

那么除了递归的边界，我们就可以将刚刚的步骤进行书写即可。

我们将每一步转换为代码书写出来：

1）1、2、……、n-1（A->B）

hanoi(n-1, a, c, b);

2）n（A->C）

move(a, c);

3）1、2、……、n-1（B->C）

hanoi(n-1, b, a, c);

那么我们的递归函数也就基本完成了，完整的递归函数为如下所示

void hanoi(int n, char a, char b, char c)
{
	if(n==1)
		move(a, c);
	else{
		hanoi(n-1, a, c, b);
		move(a, c);
		hanoi(n-1, b, a, c);
	}
}

实现汉诺塔的完整代码为如下所示：

#include
void move(char x, char y)
{
	printf("%c -> %c\n", x, y);
}
void hanoi(int n, char a, char b, char c)
{
	if(n==1)
		move(a, c);
	else{
		hanoi(n-1, a, c, b);
		move(a, c);
		hanoi(n-1, b, a, c);
	}
}
int main()
{
	int n;
	scanf("%d", &n);
	hanoi(n, 'A', 'B', 'C');
	return 0;
}

我们可以试一下当n=3时的运行结果：

可以发现结果和我们刚刚的结果一样。当n等于其他值时也是正确的。

好了，如果上面的内容你没有看太懂，那么下面让我们再来看几个典例深入了解一下。

递归问题解决

几个要点

要想解决递归问题，其实无非就是找到两个重要条件。

1）递归式
2）递归边界

在上面的汉诺塔问题中，我们就是先找到当圆盘数为n时的步骤与圆盘数为n-1时的关系，这就是我们找到的递归式，然后将n等于1作为递归边界。就完美解决了一个递归的问题。

下面我们就看几个使用递归的典例来深入的理解一下：

典例

问题一：使用递归求解n的阶乘。

我们要实现的功能很简单：就是计算以下n的阶乘。

首先，我们知道 $n!=1\ast 2\ast \cdot \cdot \cdot \ast n$ ，也可以写成为 $n!=(n-1)!\ast n$，是不是将规模为n的问题转换为了规模为n-1的问题了呢？

那么我们的递归式就可以写成$func(n)=func(n-1)\ast n$，这就是我们找到的递归式，下面只需要找到递归边界就好了。

不难发现，当n=0时，$0!=1$，所以我们可以用0来作为递归的边界。

现在两个条件都有了，我们来写一下代码来实现这个函数的功能。

int func(int n)
{
	if(n==0) return 1;			//到达递归边界时的情况
	else return func(n-1)*n;	//不断地递归调用
}

问题二：使用递归求解斐波那契数列的第n项。

首先，我们先来分析一下递归式。从斐波那契数列的求解我们就很容易得到$fib(n)=fib(n-1)+fib(n-2)$。

那么我们再来看一下递归边界，因为每次递归都将问题规模从n缩小到了n-1和n-2，所以我们要考虑一下n的大小。

很容易想到，当n为1或2时，直接返回1即可。那么我们的递归边界就是1和2时。

下面是实现该功能的一个代码：

int fib(int n)
{
	if (n == 1 || n == 2) return 1;
	else return fib(n - 1) + fib(n - 2);
}

看了两个示例之后如果还是疑惑不解，可以去找一些题目自己练练手，这样效果会更好( ఠൠఠ )ﾉ