c语言基础(一)---编程入门
c语言基础(一 )
文章目录
- c语言基础(一 )
- 一.进制转换
- 1.将二进制、八进制、十六进制转换为十进制
- 2.将十进制转换为二进制、八进制、十六进制
- 3.二进制和八进制、十六进制的转换
- 二.数据存储
- 三.数据运行
一.进制转换
1.将二进制、八进制、十六进制转换为十进制
二进制、八进制和十六进制向十进制转换都非常容易,就是“按权相加”。所谓“权”,也即“位权”。
假设当前数字是 N 进制,那么:
- 对于整数部分,从右往左看,第 i 位的位权等于Ni-1
- 对于小数部分,恰好相反,要从左往右看,第 j 位的位权为N-j。
更加通俗的理解是,假设一个多位数(由多个数字组成的数)某位上的数字是 1,那么它所表示的数值大小就是该位的位权。
1) 整数部分
将八进制数字 53627 转换成十进制:
53627 = 5×8^4 + 3×8^3 + 6×8^2 + 2×8^1 + 7×8^0 = 22423(十进制)
将十六进制数字 9FA8C 转换成十进制:
9FA8C = 9×16^4 + 15×16^3 + 10×16^2 + 8×16^1 + 12×16^0 = 653964(十进制)
将二进制数字 11010 转换成十进制
11010 = 1×2^4 + 1×2^3 + 0×2^2 + 1×2^1 + 0×2^0 = 26(十进制)
2) 小数部分
将八进制数字 423.5176 转换成十进制:
423.5176 = 4×8^2 + 2×8^1 + 3×8^0 + 5×8^-1 + 1×8^-2 + 7×8^-3 + 6×8^-4 = 275.65576171875(十进制)
将二进制数字 1010.1101 转换成十进制:
1010.1101 = 1×2^3 + 0×2^2 + 1×2^1 + 0×2^0 + 1×2^-1 + 1×2^-2 + 0×2^-3 + 1×2^-4 = 10.8125(十进制)
2.将十进制转换为二进制、八进制、十六进制
将十进制转换为其它进制时比较复杂,整数部分和小数部分的算法不一样,下面我们分别讲解。
- 整数部分
十进制整数转换为 N 进制整数采用==“除 N 取余,逆序排列”==法。具体做法是:
- 将 N 作为除数,用十进制整数除以 N,可以得到一个商和余数;
- 保留余数,用商继续除以 N,又得到一个新的商和余数;
- 仍然保留余数,用商继续除以 N,还会得到一个新的商和余数;
- ……
- 如此反复进行,每次都保留余数,用商接着除以 N,直到商为 0 时为止。
把先得到的余数作为 N 进制数的低位数字,后得到的余数作为 N 进制数的高位数字,依次排列起来,就得到了 N 进制数字。
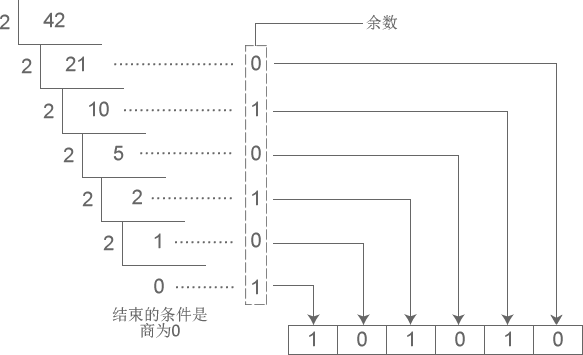
下图演示了将十进制数字 42 转换成二进制的过程:
从图中得知,十进制数字 42 转换成二进制的结果为 101010。
- 小数部分
十进制小数转换成N 进制 小数采用==“乘 N 取整,顺序排列”==法。具体做法是:
- 用 N 乘以十进制小数,可以得到一个积,这个积包含了整数部分和小数部分;
- 将积的整数部分取出,再用 N 乘以余下的小数部分,又得到一个新的积;
- 再将积的整数部分取出,继续用 N 乘以余下的小数部分;
- ……
- 如此反复进行,每次都取出整数部分,用 N 接着乘以小数部分,直到积中的小数部分为 0,或者达到所要求的精度为止。
把取出的整数部分按顺序排列起来,先取出的整数作为 N 进制小数的高位数字,后取出的整数作为低位数字,这样就得到了 N 进制小数。
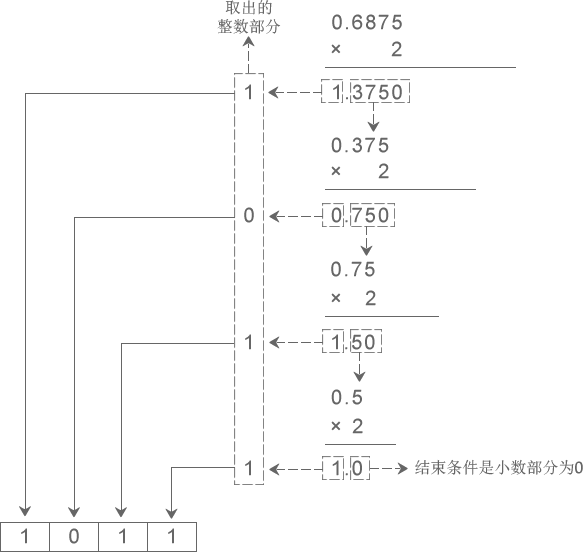
下图演示了将十进制小数 0.6875 转换成二进制小数的过程:
从图中得知,十进制小数 0.6875 转换成二进制小数的结果为 0.1011。
如果一个数字既包含了整数部分又包含了小数部分,那么将整数部分和小数部分开,分别按照上面的方法完成转换,然后再合并在一起即可。例如:
- 十进制数字 36926.930908203125 转换成八进制的结果为 110076.7345;
- 十进制数字 42.6875 转换成二进制的结果为 101010.1011。
下表列出了前 17 个十进制整数与二进制、八进制、十六进制的对应关系:
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 二进制 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 |
| 八进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 20 |
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
注意,十进制小数转换成其他进制小数时,结果有可能是一个无限位的小数。请看下面的例子:
- 十进制 0.51 对应的二进制为 0.100000101000111101011100001010001111010111…,是一个循环小数;
- 十进制 0.72 对应的二进制为 0.1011100001010001111010111000010100011110…,是一个循环小数;
- 十进制 0.625 对应的二进制为 0.101,是一个有限小数。
3.二进制和八进制、十六进制的转换
二进制整数和八进制整数之间的转换
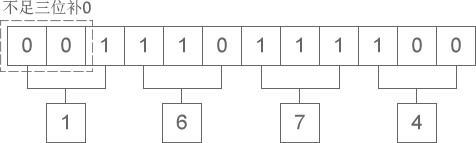
1 二进制整数转换为八进制整数时,每三位二进制数字转换为一位八进制数字,运算的顺序是从低位向高位依次进行,高位不足三位用零补齐。下图演示了如何将二进制整数 1110111100 转换为八进制:
从图中可以看出,二进制整数 1110111100 转换为八进制的结果为 1674。
2 八进制整数转换为二进制整数时,思路是相反的,每一位八进制数字转换为三位二进制数字,运算的顺序也是从低位向高位依次进行。下图演示了如何将八进制整数 2743 转换为二进制:
从图中可以看出,八进制整数 2743 转换为二进制的结果为 10111100011。
二进制整数和十六进制整数之间的转换
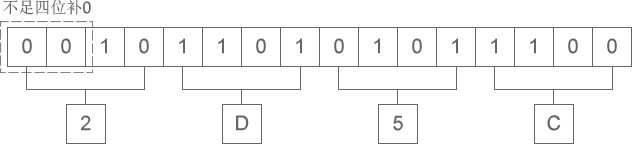
1 二进制整数转换为十六进制整数时,每四位二进制数字转换为一位十六进制数字,运算的顺序是从低位向高位依次进行,高位不足四位用零补齐。下图演示了如何将二进制整数 10 1101 0101 1100 转换为十六进制:
从图中可以看出,二进制整数 10 1101 0101 1100 转换为十六进制的结果为 2D5C。
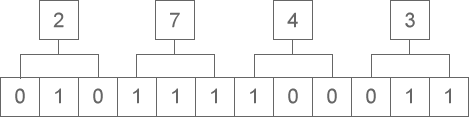
2 十六进制整数转换为二进制整数时,思路是相反的,每一位十六进制数字转换为四位二进制数字,运算的顺序也是从低位向高位依次进行。下图演示了如何将十六进制整数 A5D6 转换为二进制:
从图中可以看出,十六进制整数 A5D6 转换为二进制的结果为 1010 0101 1101 0110。
二.数据存储
计算机要处理的信息是多种多样的,如数字、文字、符号、图形、音频、视频等,这些信息在人们的眼里是不同的。但对于计算机来说,它们在内存中都是一样的,都是以二进制的形式来表示。
要想学习编程,就必须了解二进制,它是计算机处理数据的基础。
内存条是一个非常精密的部件,包含了上亿个电子元器件,它们很小,达到了纳米级别。这些元器件,实际上就是电路;电路的电压会变化,要么是 0V,要么是 5V,只有这两种电压。5V 是通电,用1来表示,0V 是断电,用0来表示。所以,一个元器件有2种状态,0 或者 1。
我们通过电路来控制这些元器件的通断电,会得到很多0、1的组合。例如,8个元器件有 28=256 种不同的组合,16个元器件有 216=65536 种不同的组合。虽然一个元器件只能表示2个数值,但是多个结合起来就可以表示很多数值了。
我们可以给每一种组合赋予特定的含义,例如,可以分别用 1101000、00011100、11111111、00000000、01010101、10101010 来表示 C、语、言、中、文、网 这几个字,那么结合起来 1101000 00011100 11111111 00000000 01010101 10101010 就表示”C语言中文网“。
一般情况下我们不一个一个的使用元器件,而是将8个元器件看做一个单位,即使表示很小的数,例如 1,也需要8个,也就是 00000001。
1个元器件称为1比特(Bit)或1位,8个元器件称为1字节(Byte),那么16个元器件就是2Byte,32个就是4Byte,以此类推:
- 8×1024个元器件就是1024Byte,简写为1KB;
- 8×1024×1024个元器件就是1024KB,简写为1MB;
- 8×1024×1024×1024个元器件就是1024MB,简写为1GB。
单位换算:
- 1Byte = 8 Bit
- 1KB = 1024Byte = 210Byte
- 1MB = 1024KB = 220Byte
- 1GB = 1024MB = 230Byte
- 1TB = 1024GB = 240Byte
- 1PB = 1024TB = 250Byte
- 1EB = 1024PB = 260Byte
我们平时使用计算机时,通常只会设计到 KB、MB、GB、TB 这几个单位,PB 和 EB 这两个高级单位一般在大数据处理过程中才会用到。
你看,在内存中没有abc这样的字符,也没有gif、jpg这样的图片,只有0和1两个数字,计算机也只认识0和1。所以,计算机使用二进制,而不是我们熟悉的十进制,写入内存中的数据,都会被转换成0和1的组合。
三.数据运行
如果你的电脑上安装了QQ,你希望和好友聊天,会双击QQ图标,打开QQ软件,输入账号和密码,然后登录就可以了。
那么,QQ是怎么运行起来的呢?
首先,有一点你要明确,你安装的QQ软件是保存在硬盘中的。
双击QQ图标,操作系统就会知道你要运行这个软件,它会在硬盘中找到你安装的QQ软件,将数据(安装的软件本质上就是很多数据的集合)复制到内存。对!就是复制到内存!QQ不是在硬盘中运行的,而是在内存中运行的。
为什么呢?因为内存的读写速度比硬盘快很多。
对于读写速度,内存 > 固态硬盘 > 机械硬盘。机械硬盘是靠电机带动盘片转动来读写数据的,而内存条通过电路来读写数据,电机的转速肯定没有电的传输速度(几乎是光速)快。虽然固态硬盘也是通过电路来读写数据,但是因为与内存的控制方式不一样,速度也不及内存。
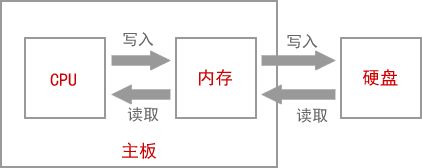
所以,不管是运行QQ还是编辑Word文档,都是先将硬盘上的数据复制到内存,才能让CPU来处理,这个过程就叫作载入内存(Load into Memory)。完成这个过程需要一个特殊的程序(软件),这个程序就叫做加载器(Loader)。
CPU直接与内存打交道,它会读取内存中的数据进行处理,并将结果保存到内存。如果需要保存到硬盘,才会将内存中的数据复制到硬盘。
例如,打开Word文档,输入一些文字,虽然我们看到的不一样了,但是硬盘中的文档没有改变,新增的文字暂时保存到了内存,Ctrl+S才会保存到硬盘。因为内存断电后会丢失数据,所以如果你编辑完Word文档忘记保存就关机了,那么你将永远无法找回这些内容。
虚拟内存
如果我们运行的程序较多,占用的空间就会超过内存(内存条)容量。例如计算机的内存容量为2G,却运行着10个程序,这10个程序共占用3G的空间,也就意味着需要从硬盘复制 3G 的数据到内存,这显然是不可能的。
操作系统(Operating System,简称 OS)为我们解决了这个问题:当程序运行需要的空间大于内存容量时,会将内存中暂时不用的数据再写回硬盘;需要这些数据时再从硬盘中读取,并将另外一部分不用的数据写入硬盘。这样,硬盘中就会有一部分空间用来存放内存中暂时不用的数据。这一部分空间就叫做虚拟内存(Virtual Memory)。
3G - 2G = 1G,上面的情况需要在硬盘上分配 1G 的虚拟内存。
硬盘的读写速度比内存慢很多,反复交换数据会消耗很多时间,所以如果你的内存太小,会严重影响计算机的运行速度,甚至会出现”卡死“现象,即使CPU强劲,也不会有大的改观
总结:CPU直接从内存中读取数据,处理完成后将结果再写入内存。