2020大一寒假ACM培训⑤（GCD&&快速幂篇）

鸽了一个月，我终于记起了我还没写完的寒假acm培训博客，相当于复习啦。
这篇主要讲的是初级数论中gcd函数，lcm函数以及快速幂取模的知识。
预备知识：
%求与符号,a%b=r,a=kb+r
| 整除符号,a|b,表示a能整除b,即b=ka,b%a==0
同余符号, 为一个同余式，表示a%c=b%c

取模运算的运算规则:
(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p) % p
(a * b) % p = (a % p * b % p) % p
a ^ b % p = ((a % p)^b) % p

一、gcd（最大公约数）

实现方法：(本文只写了欧几里得算法)

1.非递归法：

int gcd(int a,int b)
{
    int r=a%b;
    while(r)
    {
        a=b;
        b=r;
        r=a%b;
    }
    return b;
}

2.递归法：

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}

3.调用函数法
c++内置了gcd函数，使用方法：_gcd(a,b)

二、lcm（最小公倍数）

最小公倍数是可以通过先求最大公约数得到的。（敲重点）

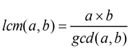
为了防止溢出可写为

补充：gcd的一些性质：
gcd(a , b) = gcd(b , a-b)
gcd(ma , mb) = m*gcd(a , b), m为一个自然数
gcd(a+mb , b) = gcd(a , b)
m=gcd(a , b) 则gcd(a/m,b/m)=gcd(a,b)/m
gcd(a, lcm(b, c)) = lcm(gcd(a, b), gcd(a, c))
lcm(a, gcd(b, c)) = gcd(lcm(a, b), lcm(a, c))
快速幂：
详细解释请看：模板 | 整数快速幂 & 快速幂取模

又到了喜闻乐见的写题时间！

nefu 1077 最大公约数和最小公倍数

#include 

using namespace std;

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}

int main()
{
    int a,b,s,p;
    while(cin>>a>>b)
    {
    s=gcd(a,b);
 p=a/gcd(a,b)*b;
 printf("%d %d\n",s,p);
    }
    return 0;
}

nefu 992 又见GCD

#include 
#include 

using namespace std;

int main()
{
    long long i,a,b,s;
    while(cin>>a>>b)
    {
    for(i=b+1;;i++)
    {
     s=__gcd(a,i);
     if(s==b)
     break;
    }
    cout<<i<<endl;
    }
    return 0;
}

nefu 764 多个数的最大公约数

#include 
#include 
using namespace std;
int main()
{
    long long x,s,b;
    while(cin>>x)
    {
    scanf("%lld",&s);
    x--;
    while(x--)
    {
    scanf("%lld",&b);
    s=__gcd(s,b);
    }
    printf("%lld\n",s);
    }
    return 0;
}

nefu 765 多个数的最小公倍数

#include 
#include 
using namespace std;

int main()
{
    long long a[15];
    long long x,gys,gbs;
    while(cin>>x)
    {
    memset(a,0,sizeof(a));
    for(int i=0;i<x;i++)
    cin>>a[i];
    for(int i=0;i<x-1;i++)
    {
    gys=__gcd(a[i],a[i+1]);
    gbs=a[i]/gys*a[i+1];
    if(i<x-2)
    a[i+1]=gbs;
    }
    printf("%lld\n",gbs);
    }
    return 0;
}

nefu 1411 LCM&GCD

#include 
#include 

using namespace std;
typedef long long ll;
ll gcd(ll a,ll  b )
{
   ll r;
    r=a%b;
    while(r)
    {
        a=b;
        b=r;
        r=a%b;
    }
    return b;
}


int main()
{
    ll b,t,x,y,f,p;
    ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
        {
            f=0;
            cin>>x>>y;
            for(ll i=x; i<=y; i++)
            {
                if(x*y%i==0)
                {b=x*y/i;
                p=gcd(b,i);
                if(b>=x&&b<=y&&p==x)
                    f++;}
            }
            printf("%lld\n",f);
        }
    return 0;
}

nefu 1221 人见人爱gcd

这题要用数学公式推导出gcd(x,y)=gcd(a,b)。(但是一开始我没推出来QAQ)
从而得到 x² + y² = a²-2 * b * gcd(a,b) （我觉得这个题更像个数学题）

#include 
#include 

using namespace std;
int  a,b,t;

int main()
{
    ios::sync_with_stdio(false);
    while(cin>>t)
    {
        while(t--)
        {cin>>a>>b;
        printf("%d\n",a*a-2*b*__gcd(a,b));
        }
    }
    return 0;
}

nefu 1669 高木同学的因子

#include 

using namespace std;
typedef long long ll;
ll x,y,k,ans,i;
int main()
{
    scanf("%lld%lld",&x,&y);
    k=__gcd(x,y);//求x，y的最大公约数k
    for( i=1;i*i<k;i++)//求k的因子数
    {
        if(k%i==0)ans+=2;
    }
        if(i*i==k)ans++;
        printf("%lld",ans);
    return 0;
}

nefu 601 快速幂取模

#include 
#include 

using namespace std;
long long a,b,c;
int main()
{
    while(scanf("%lld%lld%lld",&a,&b,&c)!=EOF)
    {
        int s=1;
        a=a%c;
        if(b==0)
        s=1%c;
        while(b)
        {
            if(b&1)
            s=(s*a)%c;
            b=b>>1;
            a=(a*a)%c;
        }
    cout<<s<<endl;
    }
    return 0;
}

nefu 1666 库特的数学题

这个题先打打表看看规律：
a[1]=6=3¹ * 2;
a[2]=18=3² * 2;
a[3]=54=3³ * 2;
a[4]=162=3⁴ * 2;
a[5]=486=3⁵ * 2;

#include 
#include 

using namespace std;
long long a,c,n;
const long long m=1e9+7;

long long mqm (long long b)
{
    int s=1;
        a=3;//快速幂的底数为3
        a=a%m;
        if(b==0)
        return 1%m;
        while(b)
        {
            if(b&1)
            s=(s*a)%m;
            b=b>>1;
            a=(a*a)%m;
        }
        return s;
}

int main()
{
    while(scanf("%lld",&n)!=EOF)
    {
        a=mqm(n);
        c=(2*a)%m;
      cout<<c<<endl;
    }
    return 0;
}

nefu 1834 异或方程解的个数

#include 

using namespace std;
int x,f;
int main()
{
    int i;
    while(scanf("%d",&x)!=EOF)
    {
        f=1;
        while(x)
        {
          if(x&1)
            f*=2;
          x=x>>1;
        }
      printf("%d\n",f);
    }
    return 0;
}