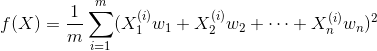传统机器学习-PCA VS LDA（线性判别分析）
PCA
1-什么是PCA
PCA是一个非监督的机器学习算法，主要用于数据将为，也可用于可视化和去噪。
第一主成分
我们想要在降维后样本保持一个比较好的区分。如何找到让样本间间距最大的轴？我们可以使用方差来代表样本间的间距（因为方差可以描述样本的疏密程度）。则问题变为找到一个轴，使得样本间的所有点映射到这个轴后，方差最大。
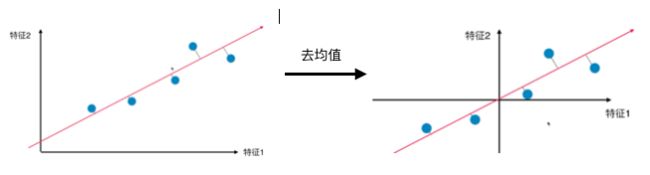
去完均值后，每一维的均值均为0，则方差由
（图一），其中均值为0，则
（图二）
对所有的样本进行demean处理
想要求一个轴的方向
使得所有样本，映射到w以后，有：
最大
2-使用梯度上升法求解PCA降维
目标：求w，使得
w的初始值不能为0，因为若w为零向量，则它的梯度也是零向量，则w值不会变化。
不能对数据进行标准化的操作，因为标准化不是线性变化，最终求出的主成分的坐标轴的方向与原始数据不一样，为了求出用户给定数据的主成分，是不能标准化的。但是我们做了去均值，这个是可以的，因为是线性变化，不影响数据的整体分布，只是相当于整个数据在坐标轴上进行了一个位移。
3-PCA最大方差理论
目标：最大化投影方差，让数据在主轴上投影的方差最大。
参照2，去均值后投影后的方差可以表示为
其中，
就是样本的协方差矩阵，将其计作
，由于w是单位向量，故有
，因此要解一个最大化问题
引入拉格朗日橙子，对w求导令其为0，可得
带入得
发现，x投影后的方差就是协方差矩阵的特征值，最大的方差就是协方差矩阵最大的特征值，最佳投影方向就是最大特征值所对应的特征向量。次最佳投影方向位于最佳投影方向的正交空间中，是第二大特征值对应的特征向量。
1）去均值
2）求样本协方差矩阵
3）对协方差矩阵进行特征值分解，将特征值从大到小排列
4）取特征值前k大对应的特征向量
，通过以下映射将n维样本映射到k维
4-求数据的前n个主成分
主成分分析法的本质是从一个坐标系转换到了另一组坐标系
其中，
是
去掉第一主成分上的分量得到的新的数据。
求出第一主成分以后，如何求出下一个主成分？
数据进行改变，将数据在第一个主成分上的分量去掉
在新的数据上求第一主成分（即原来数据的第二主成分，以此类推）
5-高维数据映射为低维数据
原数据
前k个主成分
将n维数据映射到k维，
，其中X是(m,n)，
是(m,k)，
是前k个主成分组成的矩阵，形状(n, k)，这就是数据的降维
将k维的数据还原到n维
，由于降维过程中丢失了部分信息，故恢复的数据不是原来的结果。
LDA（线性判别分析）
思想：给定训练集，设法将样本投影到一条直线上，使同类样本的投影点尽可能接近、异类样本的投影点尽可能远离。再遇到新样本时，将其投影到该直线上，再依据投影点的位置来确定类别。
二分类
两类样本的中心在直线上的投影：
，
，其中
表示第
类样本的均值向量
两类样本的协方差：
，
其中,
和
分别表示第i类样本的集合和协方差矩阵，易知、、和均是标量。
欲使同类样本的投影点尽可能接近，可以通过让同类样本的协方差矩阵尽可能小来表示，即
尽可能小；欲使异类样本的投影点进可能远离，可以通过让类中心之间的距离尽可能大表示，即
尽可能大。兼顾二者则最大化
：
我们定义“类内散度矩阵”：
我们定义“类间散度矩阵”：
则(1)式可写作：
看式(2)，我们要最大化J，我们注意到分子分母均是实数，且若
是解（可使J取到最大值），则
也是一个解，即(2)式的解与的模无关，则我们可放心的对其进行缩放，此处为了方便，我们令
，则最大化（2）式中的J等价于：
带约束的最优化问题，使用拉格朗日乘子：
对(4)关于求偏导：
要求解（5），我们注意到
，其中 
是标量，也即
的方向恒为
，（5）式若为其中一个解，则也是一个解，不妨令
，将带入（5）得：
问题转换成求解
的逆。考虑到数值稳定性，实践中我们通常对进行SVD分解，得到
，再由
得到
。最终我们可推得：
。
LDA VS PCA
1、相同点
（1）均可以对数据进行降维
（2）两者都假设符合高斯分布
2、不同点
（1）LDA是有监督的降维方法（利用了样本的标签），PCA是无监督的（没有涉及到样本的标签）。
（2）LDA降维最多降到类别数K-1的维数，PCA没有这个限制。
（3）LDA更依赖均值，如果样本信息更依赖方差的话，效果将没有PCA好。
（4）LDA可能会过拟合数据。
总体来说，PCA是为了去除原始数据集中冗余的维度，让投影子空间的各个维度的方差尽可能大，也就是熵尽可能大，再降维的同时尽量保留原数据的良好的区分度。LDA是通过数据降维找到那些具有discriminative的维度，使得原始数据在这些维度上的投影，不同类别尽可能区分开来。
参考：百面机器学习
慕课网波波老师的视频
机器学习（周志华）