灰度图形态学运算知识点总结 gray-scale morphology
一般, 结构元素B是flat.
1. 腐蚀
f以正无穷大扩边, 选取B覆盖f区域中的最小值.
2. 膨胀
f以负无穷大扩边, 选取B覆盖f区域中的最大值.
3. 开运算
先腐蚀后膨胀.
开运算会抑制小size的白点(高灰度对象).
4. 闭运算
先膨胀后腐蚀.
闭运算会填充小size的黑洞(低灰度对象).
5. 腐蚀,膨胀,开,闭的一维仿真
四种运算的仿真代码:
%% 灰度图形态学运算
clc;close all;clear;
x=1:600;
y=2*sin(0.01*x)+sin(0.02*x)+sin(0.04*x);
SELen=51; % odd number
SE=ones(1,SELen);
%% 腐蚀运算
y_erosion=nan(size(y));
for i=1:length(y)
h=max(1,i-floor(SELen/2));
t=min(length(y),i+floor(SELen/2));
y_erosion(i)=min(y(h:t));
end
%% 膨胀
y_dilation=nan(size(y));
for i=1:length(y)
h=max(1,i-floor(SELen/2));
t=min(length(y),i+floor(SELen/2));
y_dilation(i)=max(y(h:t));
end
%% 开运算
y_open=y_erosion; % 先腐蚀后膨胀
for i=1:length(y_erosion)
h=max(1,i-floor(SELen/2));
t=min(length(y_erosion),i+floor(SELen/2));
y_open(i)=max(y_erosion(h:t));
end
%% 闭运算
y_close=y_dilation; % 先膨胀后腐蚀
for i=1:length(y_dilation)
h=max(1,i-floor(SELen/2));
t=min(length(y_dilation),i+floor(SELen/2));
y_close(i)=min(y_dilation(h:t));
end
figure;plot(x,y,'r-',x,y_erosion,'g-',x,y_dilation,'b-');
xlabel('点序号');ylabel('灰度值');legend('原曲线','腐蚀','膨胀');
figure;plot(x,y_open,'r-',x,y_close,'b-');
xlabel('点序号');ylabel('灰度值');
legend('开','闭');
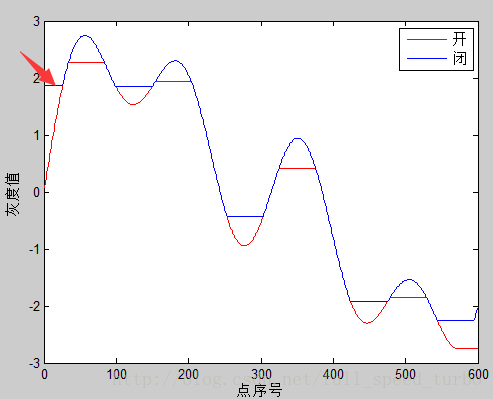
注意: 闭运算曲线开头处, 是一段水平线, 没有和原曲线重合. 和DIP书中不一致.
使用Matlab的内置函数验证一下:
%% 内置灰度形态运算
clc;close all;clear;
x=1:600;
y=2*sin(0.01*x)+sin(0.02*x)+sin(0.04*x);
SELen=51; % odd number
SE = strel('line', 50, 0);
%% imerode imdilate
y_imerode=imerode(y,SE);
y_imdilate=imdilate(y,SE);
%% imclose 闭运算
y_imclose = imclose(y,SE);
%% imopen 开运算
y_imopen=imopen(y,SE);
%% plot
figure;plot(x,y,'r-',x,y_imerode,'g-',x,y_imdilate,'b-');
xlabel('点序号');ylabel('灰度值');legend('原曲线','imerode','imdilate');
figure;plot(x,y_imopen,'r-',x,y_imclose,'b-');
legend('imopen','imclose');结果和上面的完全一致.
6. 形态学平滑
a. 对于噪声灰度高于背景灰度的情形, 先开后闭. 因为开运算会抑制小size的白点(高灰度对象). 或者连续地先开后闭运算, SE逐渐增大.
b. 对于噪声灰度低于背景灰度的情形, 先闭后开. 因为闭运算会填充小size的黑洞(低灰度对象).也可以连续操作.
7. 形态学梯度
膨胀减去腐蚀.
8. top-hat
原图减去开运算
9. bottom-hat
闭运算减去原图.
top-hat和bottom-hat 可以用于移除背景, 校正不均匀光照.
可以作为分割的前处理.
10. 粒度分析 Granulometry
统计相同形状不同size的粒子位置和数量.
a. 先做形态平滑.
b. 使用逐渐增大的SE做opening.
c. 不同尺度SE的opening结果求差分.
d. 差分曲线有较大尖峰的地方就是提取的相应size的粒子.
11. 文本分割 Textual Segment
和粒度分析类似.
a. 先用闭运算把较小的黑洞填平. SE大小要合适.
b. 使用开运算把较大黑洞连成一片. 形成了界限分明的两个区域.
c. 使用形态梯度算法提取边界.
12. 形态学重建
形态学重建运算比简单的形态学运算好的地方在于:
a. 对背景的提取较为完整干净.
b. 对前景(对象)的保留较为完整.

