C语言四种方法求最大公约数

一、实验要求

运行最大公约数的常用算法，并进行程序的调试与测试，要求程序设计风格良好，并添加异常处理模块。

二、实验方法（四种）

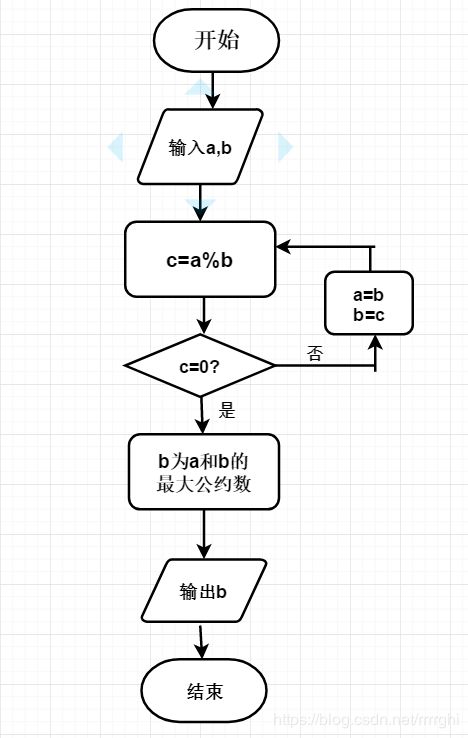
1.辗转相除法（欧几里德法） C语言中用于计算两个正整数a,b的最大公约数，采用函数嵌套调用形式进行求两个数的最大公约数。其算法过程为：

前提：设两数为a,b设其中a做被除数,b做除数,temp为余数

Steps:大数放a中，小数放b中；

求a/b的余数；

若temp=0则b为最大公约数；

如果temp!=0则把b的值给a,temp的值给a；

返回第二步。

流程图：

2、穷举法（枚举法）

从两个数中较小数开始由大到小列举，直到找到公约数立即中断列举，得到的公约数便是最大公约数。

流程图：

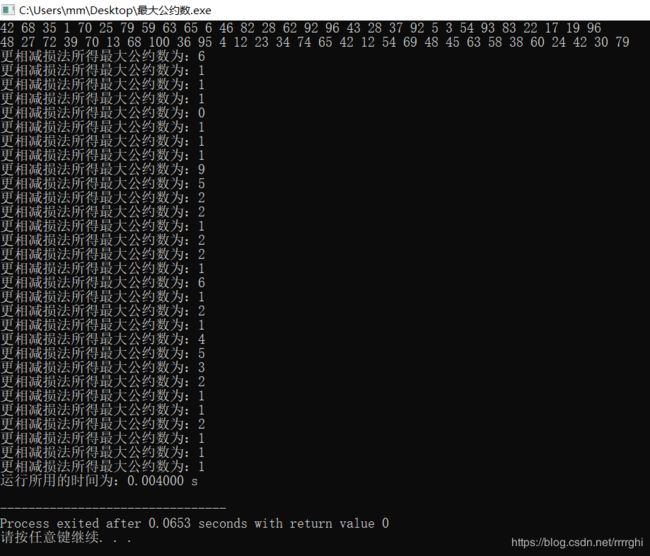
3、更相减损法

Steps：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步；

以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。

则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
流程图：

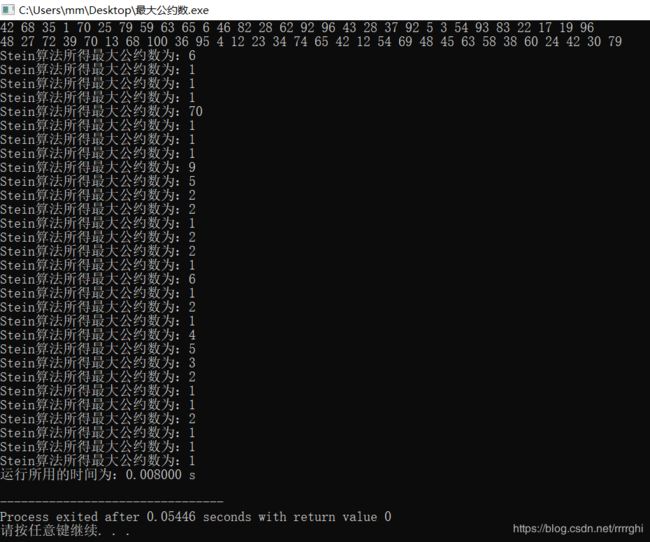
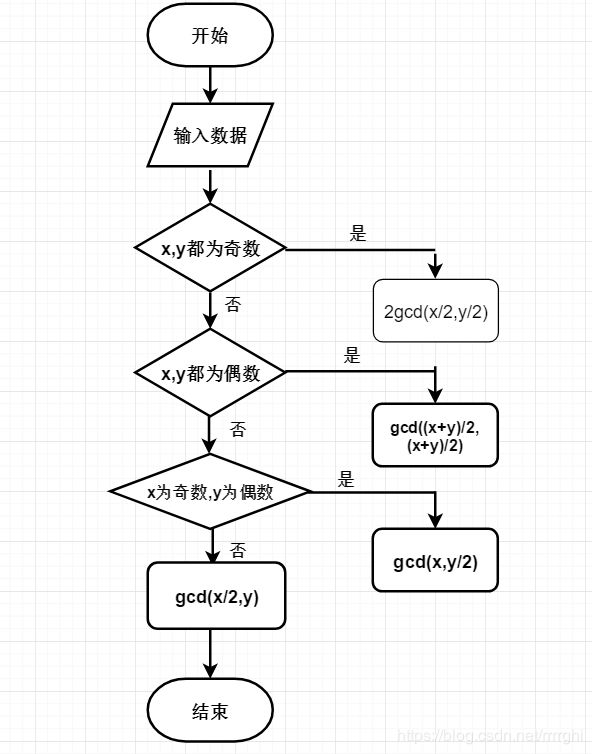
4、Stein算法

性质：gcd(kx,ky)=k*gcd(x,y)

对两个正整数 x>y

均为偶数 gcd(x,y)=2gcd(x/2,y/2);

均为奇数 gcd(x,y)=gcd((x+y)/2,(x-y)/2);

X奇 y偶 gcd(x,y)=gcd(x,y/2);

X偶 y奇 gcd(x,y)=gcd(x/2,y)
或 gcd(x,y)=gcd(y,x/2).
流程图：

三、算法实现

//C语言实现 四种方法求最大公约数 

// 2019 03

// WANTING WANG

#include

#include

#include

#include

//辗转相除法 

 int gcd(int a,int b)

 { 
     if(a%b==0)
     return b;
         else;
         return gcd(b,a%b);
 }


//穷举法

 int divisor (int a, int b) //自定义函数求两数的最大公约数

 {
      int  temp;//定义整型变量
     temp=(a>b)?b:a;//采种条件运算表达式求出两个数中的最小值
     while(temp>0)

      {
              if(a%temp==0&&b%temp==0)//只要找到一个数能同时被a,b所整除，则中止循环
              break;
              temp--;//如不满足if条件则变量自减，直到能被a,b所整除 
      } 
     return (temp);//返回满足条件的数到主调函数处 
  } 

//更相减损法
 int gcd2(int m,int n)
 {
     int i=0,temp,x;
     while(m%2==0&&n%2==0)//判断m和n能被多少个2整除
    {
         m/=2;
         n/=2;
         i+=1;
    } 
     if(mx)?n:x;
        n=(n> 1;
                                x -= y;
                        }
                        else
                        {/* when x is odd and y is even */
                                y >>= 1;
                        }
                }
                else
                {/* when x is even */
                        if ( y & 0x1 )
                        {/* when x is even and y is odd */
                                x >>= 1;
                                if ( x < y )
                                {
                                        temp = x;
                                        x = y;
                                        y = temp;
                                }
                        }
                        else
                        {/* when x and y are both even */
                                x >>= 1;
                                y >>= 1;
                                ++factor;
                        }
                }
        }
        return ( x << factor );
}


int main()
{
      int i;     
      int a[30];
      for(i=0;i<30;i++)
     {
             a[i]=rand()%100 + 1;
             printf("%d ",a[i]);
      }
       printf("\n");
       int b[30];
       for(i=0;i<30;i++)
      {
         b[i]=rand()%100 + 1;
         printf("%d ",b[i]);
      }
      printf("\n");
      clock_t start,finish;
      double dur;
      start= clock();
      for(i=0;i<30;i++)
    {
        //printf("辗转相除法所得最大公约数为：%d\n",gcd(a[i],b[i]));
        //printf("穷举法所得最大公约数为：%d\n",divisor(a[i],b[i]));
          printf("更相减损法所得最大公约数为：%d\n",gcd2(a[i],b[i]));
        //printf("Stein算法所得最大公约数为：%d\n",Stein(a[i],b[i]));
    }
 finish=clock();
 dur=(double)(finish-start)/CLOCKS_PER_SEC;
 printf("运行所用的时间为：%lf s\n",dur); 
    return 0;
 }

四、测试