The CMA(Covariance matrix Adaptation) Evolution Strategy
The CMA Evolution Strategy
最近,学习一些优化算法,看到一种自适应协方差矩阵进化算法,抽点时间研究一下。CMA是一种随机的,不需要计算梯度的数值优化算法。主要用来解决非线性、非凸的优化问题,属于进化算法的一类,具有随机性。本文主要翻译的:The CMA Evolution Strategy: A Tutorial,代码参见CMA-ES主页,个人理解,欢迎批评指针。
主要内容如下:
- 前言知识
- CMA-ES 算法
- matlab代码 解释
1、前言知识
- 正定矩阵的特征分解
- 多元正态分布
- 随机优化
- Hessian矩阵和协方差矩阵
正定矩阵的特征分解
正定对称矩阵C ,对于任意一个不为0的向量x,都有 xTCx>0 x T C x > 0 。矩阵C有标准的正交向量 B=[b1,...,bn] B = [ b 1 , . . . , b n ] ,特征值 d12,...dn2>0 d 1 2 , . . . d n 2 > 0 。
即: Cbi=di2bi C b i = d i 2 b i
标准的正交向量矩阵 BTB=I B T B = I
C的正交分解
C−1=(BD2BT)−1=BT−1D−2B−1=BD−2BT=B⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢1d21⋮⋮⋮⋯1d22⋮⋮⋯⋯⋱⋯⋯⋯⋮1d2n⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥BT C − 1 = ( B D 2 B T ) − 1 = B T − 1 D − 2 B − 1 = B D − 2 B T = B [ 1 d 1 2 ⋯ ⋯ ⋯ ⋮ 1 d 2 2 ⋯ ⋯ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ ⋯ 1 d n 2 ] B T
其中:
D2=DD=diag(d1,...,dn)2=diag(d12,.....dn2) D 2 = D D = d i a g ( d 1 , . . . , d n ) 2 = d i a g ( d 1 2 , . . . . . d n 2 )
di d i 是特征值的平方根。协方差矩阵是个半正定的矩阵。
多元正态分布
多元正态分布 N(m,C) N ( m , C ) ,m是均值,C是协方差。
对于一个二维向量x和一个正定实对称矩阵C,方程 xTCx=D x T C x = D ,其中D是常量,描述了一个中心在原点的椭圆。(参考PCA的相关知识)
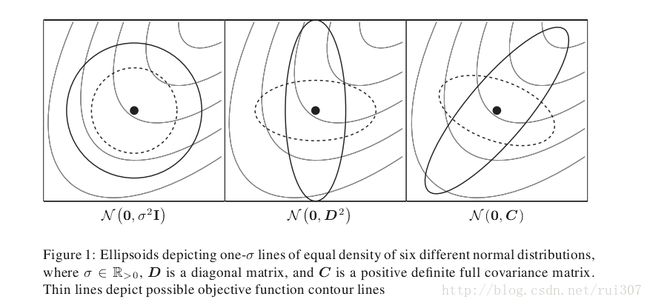
中心在原点的椭圆协方差矩阵的几何解释如下图:椭圆的主轴对应协方差的特征向量,主轴长度对应于协方差的特征值的大小。特征分解 C=BD2BT C = B D 2 B T 。如果 D=δI D = δ I , C=δI C = δ I ,此时如下图左,描述的是一个圆。假如,B=I, C=D2 C = D 2 ,此时如图(中),椭圆的主轴平行于坐标(或垂直)。
正态分布 N(m,C) N ( m , C ) 能够写成不同的形式:
N(m,C) N ( m , C ) ~ m+N(0,C) m + N ( 0 , C )
~ m+C12N(0,I) m + C 1 2 N ( 0 , I )
~ m+BDBTN(0,I) m + B D B T N ( 0 , I )
~ m+BDN(0,I) m + B D N ( 0 , I )
上式可以用来计算正态分布的向量。 其中,BTN(0,I) 其 中 , B T N ( 0 , I ) ~ N(0,I) N ( 0 , I )
黑箱随机优化
考虑一个黑箱搜索情景,想要最小化代价函数,目标是寻找一个或者多个点x,使得函数 f(x) f ( x ) 尽可能的小。而黑箱搜索,所能提供的信息只有函数 f(x) f ( x ) 。搜索点可以自由的选择。但是同时意味着大的搜索信息量。
- f:x f : x → f(x) f ( x )
一个随机优化的流程如下:
初始化分布参数 θ θ
迭代代数 g:0,1,2,……
- 从分布中采样n个独立的点 P(x/θ(g)) P ( x / θ ( g ) ) → x1,...,xn x 1 , . . . , x n
- 利用 f(x) f ( x ) 评估样本 x1,...,xn x 1 , . . . , x n
- 更新参数 θ(g+1)=Fθ(θ(g),(x1,f(x1)),...,(xn,f(xn))) θ ( g + 1 ) = F θ ( θ ( g ) , ( x 1 , f ( x 1 ) ) , . . . , ( x n , f ( x n ) ) )
- 中断条件满足,结束
在CMA进化算法中,分布函数P是一个多元正态分布。在给定均值和协方差后,正态分布具有最大的熵。
Hessian矩阵和协方差矩阵
一个凸二次目标函数 fH:x f H : x → 12xTHx 1 2 x T H x ,其中,H是Hessian矩阵(简单理解为二阶导),是个正定矩阵。在我们搜索的分布函数正态分布 N(m,C) N ( m , C ) 中,C与H有相近的关系。前面推导中: BTC−1B=D2,D2是个对角阵 B T C − 1 B = D 2 , D 2 是 个 对 角 阵 ,假如H=C=I, fH f H 等同于优化函数 f(x)=12xTx f ( x ) = 1 2 x T x 。,设置 C−1=H C − 1 = H ,在凸二次规划,设置搜索分布的协方差矩阵等于Hession矩阵的逆矩阵等同于把一个椭球函数缩放到一个球面上。因此认为协方差矩阵优化等同于Hessian矩阵逆矩阵的优化。进一步,选择协方差矩阵或者选择一个线性仿射变化对于搜索空间是等价的。因为对于所有满秩的N X N的矩阵A,我们都能找到一个正定Hession矩阵。
例如:
最终,CMA的目标是尽可能的估计目标函数的等高线。例如,上图最右边的实线图,目标函数的等高线图最适合,可以简单的预测它能够最易于帮助目标优化。
2、CMA-ES
- 采样
- 选择策略,参数更新
- 自适应协方差矩阵
- 控制步长
采样
CMA算法从多元正态分布中采样:
每一代 g=0,1,2.... g = 0 , 1 , 2.... :

公式中 δ(g) δ ( g ) 为步长,与样本标准差有关系。
选择策略,参数更新
均值 m(g+1) m ( g + 1 ) 通过采用数据 x(g+1)1,...,x(g+1)λ x 1 ( g + 1 ) , . . . , x λ ( g + 1 ) 的加权均值来更新。上面的公式中,从 λ λ 个后代中选取 μ μ 个权重最大的作为更新均值的样本数据。
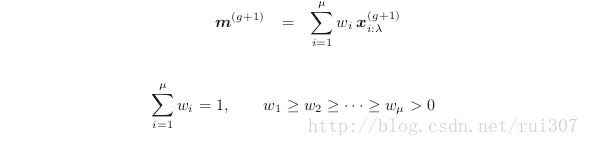

后代方差有效性选择的数量 λeff λ e f f 计算( 1<=λeff<=μ 1 <= λ e f f <= μ )。通常, λeff≈λ/4 λ e f f ≈ λ / 4 是一个合理的值:
λeff=(||ω||1||ω||2)2=(∑μi=1|ω|)2∑μi=1ω2=1∑μi=1ω2 λ e f f = ( | | ω | | 1 | | ω | | 2 ) 2 = ( ∑ i = 1 μ | ω | ) 2 ∑ i = 1 μ ω 2 = 1 ∑ i = 1 μ ω 2均值 m(g+1) m ( g + 1 ) 的更新公式为:
m(g+1)=m(g)+cm∑i=1μωi(x(g+1)i:λ−m(g)) m ( g + 1 ) = m ( g ) + c m ∑ i = 1 μ ω i ( x i : λ ( g + 1 ) − m ( g ) )
其中: cm<=1 c m <= 1 代表学习率,通常设置为1.
自适应协方差矩阵
1、 估计协方差矩阵
估计协方差矩阵需要用到均值:一种是利用子代的所有采样计算均值,另一种是利用上一代的均值计算协方差。

为了更好的估计方差,要利用到权重选择的机制,选择 μ μ 个子代,协方差更新如下式:
C(g+1)μ=∑i=1μωi(x(g+1)i:λ−m(g))(x(g+1)i:λ−m(g))T C μ ( g + 1 ) = ∑ i = 1 μ ω i ( x i : λ ( g + 1 ) − m ( g ) ) ( x i : λ ( g + 1 ) − m ( g ) ) T
为了保证上面估计的可靠性, μeff μ e f f 要足够大,一般约等于优化函数维度的10倍。
对于一般的多元正太分布算法(EMNA),利用当前代的均值估计,其中 m(g+1)=1μ∑μi=1x(g+1)i:λ m ( g + 1 ) = 1 μ ∑ i = 1 μ x i : λ ( g + 1 ) :
C(g+1)EMNAglobal=1μ∑i=1μωi(x(g+1)i:λ−m(g+1))(x(g+1)i:λ−m(g+1))T C E M N A g l o b a l ( g + 1 ) = 1 μ ∑ i = 1 μ ω i ( x i : λ ( g + 1 ) − m ( g + 1 ) ) ( x i : λ ( g + 1 ) − m ( g + 1 ) ) T2、 Rank−μ−Update R a n k − μ − U p d a t e
更新 μ μ 个子代的协方差与EMNA对比如下图,图像右上角为目标函数优化的方向(min f(x))。

协方差矩阵的迭代更新策略: cμ<=1,是迭代更新率,具体更新用上一代的协方差和当前代的选择μ个样本更新后的协方差做指数平滑 c μ <= 1 , 是 迭 代 更 新 率 , 具 体 更 新 用 上 一 代 的 协 方 差 和 当 前 代 的 选 择 μ 个 样 本 更 新 后 的 协 方 差 做 指 数 平 滑 (注:具体实现参见原文)
C(g+1)=(1−cμ)C(g)+cμ1(δ(g))2C(g+1)μ C ( g + 1 ) = ( 1 − c μ ) C ( g ) + c μ 1 ( δ ( g ) ) 2 C μ ( g + 1 )
cμ c μ 的选择是至关重要的,小的值可能导致学习比较慢,大的值可能导致协方差矩阵的退化,前一代的信息丢失过多。实验表明当n比较大时, cμ=μeff/n2 c μ = μ e f f / n 2 是一个比较好的选择。3、 Rank−one−Update R a n k − o n e − U p d a t e
考虑 Rank−μ−Update R a n k − μ − U p d a t e 中的协方差更新式子中,假设μ个子代取1,更新公式变为:
C(g+1)=(1−c1)C(g)+c1(x(g+1)i:λ−m(g)δ(g))(x(g+1)i:λ−m(g)δ(g))T C ( g + 1 ) = ( 1 − c 1 ) C ( g ) + c 1 ( x i : λ ( g + 1 ) − m ( g ) δ ( g ) ) ( x i : λ ( g + 1 ) − m ( g ) δ ( g ) ) T
用 y(g+1)=(x(g+1)i:λ−mg)/δ(g) y ( g + 1 ) = ( x i : λ ( g + 1 ) − m g ) / δ ( g ) ;
C(g+1)=(1−c1)C(g)+c1y(g+1)y(g+1)T C ( g + 1 ) = ( 1 − c 1 ) C ( g ) + c 1 y ( g + 1 ) y ( g + 1 ) T
接下来提出进化路径,上式中利用 y(g+1)y(g+1)T y ( g + 1 ) y ( g + 1 ) T 更新协方差矩阵,对于连续的许多代,进化路径可以表达成进化路径的叠加,个人理解为增强每2代中心点变化的方向协方差,使进化方向朝此方向运动:
m(g+1)−m(g)δ(g)+m(g)−m(g−1)δ(g−1)+m(g−1)−m(g−2)δ(g−2) m ( g + 1 ) − m ( g ) δ ( g ) + m ( g ) − m ( g − 1 ) δ ( g − 1 ) + m ( g − 1 ) − m ( g − 2 ) δ ( g − 2 )
进化路径的解释如图:

实际中进化路径用指数平滑的更新策略:

最后 Rank−one−Update R a n k − o n e − U p d a t e 利用进化路径 p(g+1)c p c ( g + 1 ) 协方差的更新策略:
C(g+1)=(1−c1)C(g)+c1p(g+1)cp(g+1)cT C ( g + 1 ) = ( 1 − c 1 ) C ( g ) + c 1 p c ( g + 1 ) p c ( g + 1 ) T
结合 Rank−one−Update R a n k − o n e − U p d a t e 和 Rank−μ−Update R a n k − μ − U p d a t e 的协方差更新策略见下图:

控制步长调整
(待更新……)
3、matlab代码
下面是CMA-ES的MATLAB代码,来自hansen的源码。
function xmin=purecmaes
% (mu/mu_w, lambda)-CMA-ES
% CMA-ES: Evolution Strategy with Covariance Matrix Adaptation
% for nonlinear function minimization.
%
% This code is "an excerpt" from cmaes.m and implements the key
% parts of the algorithm. It is intendend to be used for READING
% and UNDERSTANDING the basic flow and all details of the CMA-ES
% *algorithm*. To run "serious" simulations better use the cmaes.m
% code: it is longer, but offers restarts, far better termination
% options, and, in particular, supposedly quite useful output.
%
% Author: Nikolaus Hansen, 2003-09.
% e-mail: hansen[at]lri.fr
%
% License: This code is released into the public domain (that is,
% you may use and modify it however you like).
%
% URL: http://www.lri.fr/~hansen/purecmaes.m
% References: See end of file. Last change: April, 29, 2014
% -------------------- Initialization --------------------------------
% User defined input parameters (need to be edited)
strfitnessfct = 'fsphere'; %优化的函数三维球体name of objective/fitness function
N = 3; % 三维球体number of objective variables/problem dimension
xmean = rand(N,1); % 初始化均值 objective variables initial point
sigma = 0.5; % 初始化标准差 coordinate wise standard deviation (step size)
stopfitness = 1e-10; % 停止优化指标stop if fitness < stopfitness (minimization)
stopeval = 1e3*N^2; % 迭代次数最大值stop after stopeval number of function evaluations
% Strategy parameter setting: Selection
lambda = 4+floor(3*log(N)); %后代数量 population size, offspring number
mu = lambda/2; % number of parents/points for recombination
weights = log(mu+1/2)-log(1:mu)'; % muXone array for weighted recombination
mu = floor(mu);
weights = weights/sum(weights); % normalize recombination weights array
mueff=sum(weights)^2/sum(weights.^2); %后代方差有效数量 variance-effectiveness of sum w_i x_i
% Strategy parameter setting: Adaptation
cc = (4 + mueff/N) / (N+4 + 2*mueff/N); % time constant for cumulation for C
cs = (mueff+2) / (N+mueff+5); % t-const for cumulation for sigma control
c1 = 2 / ((N+1.3)^2+mueff); %rank-one的学习率 learning rate for rank-one update of C
cmu = min(1-c1, 2 * (mueff-2+1/mueff) / ((N+2)^2+mueff)); % rank-mu的学习率 for rank-mu update
damps = 1 + 2*max(0, sqrt((mueff-1)/(N+1))-1) + cs; % damping for sigma
% usually close to 1
% Initialize dynamic (internal) strategy parameters and constants
pc = zeros(N,1); ps = zeros(N,1); % evolution paths for C and sigma
B = eye(N,N); % B defines the coordinate system
D = ones(N,1); % diagonal D defines the scaling
C = B * diag(D.^2) * B'; % covariance matrix C
invsqrtC = B * diag(D.^-1) * B'; % C^-1/2
eigeneval = 0; % track update of B and D
chiN=N^0.5*(1-1/(4*N)+1/(21*N^2)); % expectation of
% ||N(0,I)|| == norm(randn(N,1))
out.dat = []; out.datx = []; % for plotting output
i=0;
% -------------------- Generation Loop --------------------------------
counteval = 0; % the next 40 lines contain the 20 lines of interesting code
while counteval < stopeval
i=i+1;
% Generate and evaluate lambda offspring(随机产生后代)
for k=1:lambda,
arx(:,k) = xmean + sigma * B * (D .* randn(N,1)); % m + sig * Normal(0,C)
arfitness(k) = feval(strfitnessfct, arx(:,k)); % objective function call
counteval = counteval+1;
end
% Sort by fitness and compute weighted mean into xmean(排序,选择值较小的采样点)
[arfitness, arindex] = sort(arfitness); % minimization
xold = xmean;
xmean = arx(:,arindex(1:mu)) * weights; % recombination, new mean value(新的均值)
% Cumulation: Update evolution paths(更新进化路径,在协方差矩阵更新的时候利用,协方差更新的方法:rank one 和rank U 融合的方式)
ps = (1-cs) * ps ...
+ sqrt(cs*(2-cs)*mueff) * invsqrtC * (xmean-xold) / sigma;
hsig = sum(ps.^2)/(1-(1-cs)^(2*counteval/lambda))/N < 2 + 4/(N+1);
pc = (1-cc) * pc ...
+ hsig * sqrt(cc*(2-cc)*mueff) * (xmean-xold) / sigma;
% Adapt covariance matrix C(更新协方差矩阵)
artmp = (1/sigma) * (arx(:,arindex(1:mu)) - repmat(xold,1,mu)); % mu difference vectors
C = (1-c1-cmu) * C ... % regard old matrix
+ c1 * (pc * pc' ... % plus rank one update
+ (1-hsig) * cc*(2-cc) * C) ... % minor correction if hsig==0
+ cmu * artmp * diag(weights) * artmp'; % plus rank mu update
% Adapt step size sigma更新步长
sigma = sigma * exp((cs/damps)*(norm(ps)/chiN - 1));
% Update B and D from C
if counteval - eigeneval > lambda/(c1+cmu)/N/10 % to achieve O(N^2)
eigeneval = counteval;
C = triu(C) + triu(C,1)'; % enforce symmetry
[B,D] = eig(C); % eigen decomposition, B==normalized eigenvectors
D = sqrt(diag(D)); % D contains standard deviations now
invsqrtC = B * diag(D.^-1) * B';
end
% Break, if fitness is good enough or condition exceeds 1e14, better termination methods are advisable
if arfitness(1) <= stopfitness || max(D) > 1e7 * min(D)
break;
end
% Output
more off; % turn pagination off in Octave
disp([num2str(counteval) ': ' num2str(arfitness(1)) ' ' ...
num2str(sigma*sqrt(max(diag(C)))) ' ' ...
num2str(max(D) / min(D))]);
% with long runs, the next line becomes time consuming
out.dat = [out.dat; arfitness(1) sigma 1e5*D' ];
out.datx = [out.datx; xmean'];
end % while, end generation loop
% ------------- Final Message and Plotting Figures --------------------
disp([num2str(counteval) ': ' num2str(arfitness(1))]);
xmin = arx(:, arindex(1)); % Return best point of last iteration.
% Notice that xmean is expected to be even
% better.
figure(1); hold off; semilogy(abs(out.dat)); % abs for negative fitness
figure(2);
semilogy(out.dat(:,1) - min(out.dat(:,1)), 'k-'); % difference to best ever fitness, zero is not displayed
title('fitness, sigma, sqrt(eigenvalues)'); grid on; xlabel('iteration');
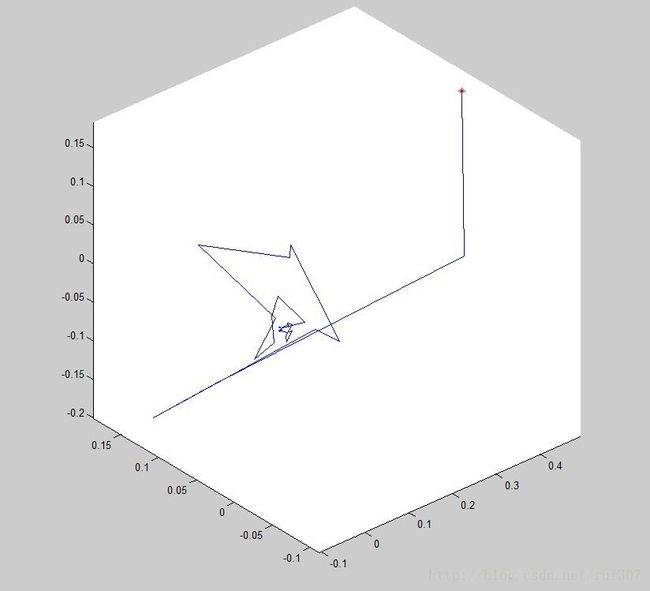
figure(3); hold off; plot(out.datx);
title('Distribution Mean'); grid on; xlabel('iteration')
figure(4)
plot3(out.datx(1,1),out.datx(1,2),out.datx(1,3),'*')
hold on
plot3(out.datx(:,1),out.datx(:,2),out.datx(:,3))
% ---------------------------------------------------------------
function f=frosenbrock(x)
if size(x,1) < 2 error('dimension must be greater one'); end
f = 100*sum((x(1:end-1).^2 - x(2:end)).^2) + sum((x(1:end-1)-1).^2);
function f=fsphere(x)
f=sum(x.^2);
function f=fssphere(x)
f=sqrt(sum(x.^2));
function f=fschwefel(x)
f = 0;
for i = 1:size(x,1),
f = f+sum(x(1:i))^2;
end
function f=fcigar(x)
f = x(1)^2 + 1e6*sum(x(2:end).^2);
function f=fcigtab(x)
f = x(1)^2 + 1e8*x(end)^2 + 1e4*sum(x(2:(end-1)).^2);
function f=ftablet(x)
f = 1e6*x(1)^2 + sum(x(2:end).^2);
function f=felli(x)
N = size(x,1); if N < 2 error('dimension must be greater one'); end
f=1e6.^((0:N-1)/(N-1)) * x.^2;
function f=felli100(x)
N = size(x,1); if N < 2 error('dimension must be greater one'); end
f=1e4.^((0:N-1)/(N-1)) * x.^2;
function f=fplane(x)
f=x(1);
function f=ftwoaxes(x)
f = sum(x(1:floor(end/2)).^2) + 1e6*sum(x(floor(1+end/2):end).^2);
function f=fparabR(x)
f = -x(1) + 100*sum(x(2:end).^2);
function f=fsharpR(x)
f = -x(1) + 100*norm(x(2:end));
function f=fdiffpow(x)
N = size(x,1); if N < 2 error('dimension must be greater one'); end
f=sum(abs(x).^(2+10*(0:N-1)'/(N-1)));
function f=frastrigin10(x)
N = size(x,1); if N < 2 error('dimension must be greater one'); end
scale=10.^((0:N-1)'/(N-1));
f = 10*size(x,1) + sum((scale.*x).^2 - 10*cos(2*pi*(scale.*x)));
function f=frand(x)
f=rand;
% ---------------------------------------------------------------
%%% REFERENCES
%
% Hansen, N. and S. Kern (2004). Evaluating the CMA Evolution
% Strategy on Multimodal Test Functions. Eighth International
% Conference on Parallel Problem Solving from Nature PPSN VIII,
% Proceedings, pp. 282-291, Berlin: Springer.
% (http://www.bionik.tu-berlin.de/user/niko/ppsn2004hansenkern.pdf)
%
% Further references:
% Hansen, N. and A. Ostermeier (2001). Completely Derandomized
% Self-Adaptation in Evolution Strategies. Evolutionary Computation,
% 9(2), pp. 159-195.
% (http://www.bionik.tu-berlin.de/user/niko/cmaartic.pdf).
%
% Hansen, N., S.D. Mueller and P. Koumoutsakos (2003). Reducing the
% Time Complexity of the Derandomized Evolution Strategy with
% Covariance Matrix Adaptation (CMA-ES). Evolutionary Computation,
% 11(1). (http://mitpress.mit.edu/journals/pdf/evco_11_1_1_0.pdf).
%