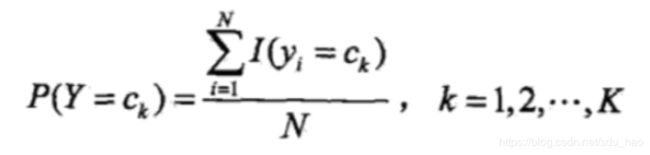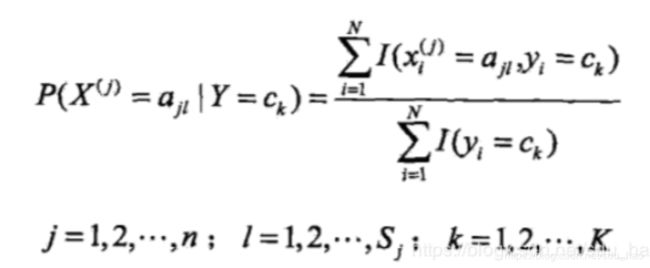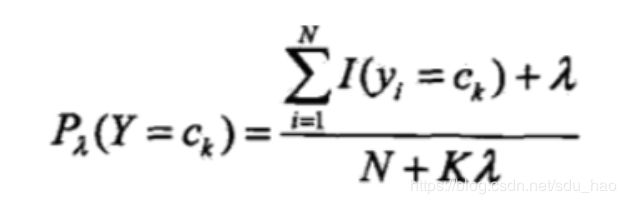李航机器学习 | (7) 统计学习方法(第2版)笔记 --- 朴素贝叶斯习题与编程作业
1. 用极大似然估计法推出朴素贝叶斯法中的概率估计公式:
2. 用贝叶斯估计法推出朴素贝叶斯法中的概率估计公式:
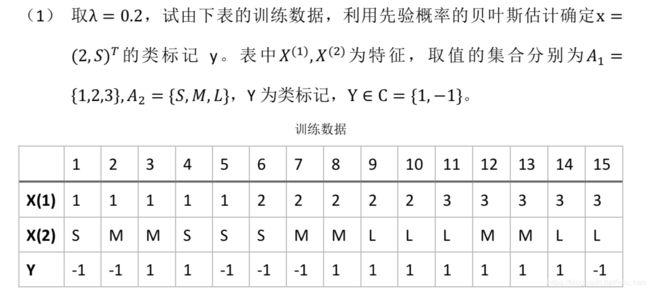
3. 贝叶斯估计求解过程
4. 自编程实现朴素贝叶斯算法,对上述表格中的训练数据进行分类。
"""
朴素贝叶斯算法的实现
2019/4/12
"""
import numpy as np
import pandas as pd
class NaiveBayes():
def __init__(self, lambda_):
self.lambda_ = lambda_ # 贝叶斯系数 取0时,即为极大似然估计 非0时为贝叶斯估计
self.y_types_count = None # y的(类型:数量)
self.y_types_proba = None # y的(类型:概率)
self.x_types_proba = dict() # (xi 的编号,xi的取值,y的类型):概率
def fit(self, X_train, y_train):
self.y_types = np.unique(y_train) # y的所有取值类型
X = pd.DataFrame(X_train) # 转化成pandas DataFrame数据格式,下同
y = pd.DataFrame(y_train)
# y的(类型:数量)统计
self.y_types_count = y[0].value_counts()
# y的(类型:概率)计算
self.y_types_proba = (self.y_types_count + self.lambda_) / (y.shape[0] + len(self.y_types) * self.lambda_)
# (xi 的编号,xi的取值,y的类型):概率的计算
for idx in X.columns: # 遍历xi
for j in self.y_types: # 选取每一个y的类型
p_x_y = X[(y == j).values][idx].value_counts() # 选择所有y==j为真的数据点的第idx个特征的值,并对这些值进行(类型:数量)统计
for i in p_x_y.index: # 计算(xi 的编号,xi的取值,y的类型):概率
self.x_types_proba[(idx, i, j)] = (p_x_y[i] + self.lambda_) / (
self.y_types_count[j] + p_x_y.shape[0] * self.lambda_)
def predict(self, X_new):
res = []
for y in self.y_types: # 遍历y的可能取值
p_y = self.y_types_proba[y] # 计算y的先验概率P(Y=ck)
p_xy = 1
for idx, x in enumerate(X_new):
p_xy *= self.x_types_proba[(idx, x, y)] # 计算P(X=(x1,x2...xd)/Y=ck)
res.append(p_y * p_xy)
for i in range(len(self.y_types)):
print("[{}]对应概率:{:.2%}".format(self.y_types[i], res[i]))
# 返回最大后验概率对应的y值
return self.y_types[np.argmax(res)]
def main():
X_train = np.array([
[1, "S"],
[1, "M"],
[1, "M"],
[1, "S"],
[1, "S"],
[2, "S"],
[2, "M"],
[2, "M"],
[2, "L"],
[2, "L"],
[3, "L"],
[3, "M"],
[3, "M"],
[3, "L"],
[3, "L"]
])
#标签
y_train = np.array([-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1])
#创建朴素贝叶斯分类器对象
clf = NaiveBayes(lambda_=0.2)
#训练 计算先验概率和条件概率
clf.fit(X_train, y_train)
#预测样本
X_new = np.array([2, "S"])
#预测
y_predict = clf.predict(X_new)
print("{}被分类为:{}".format(X_new, y_predict))
if __name__ == "__main__":
main()
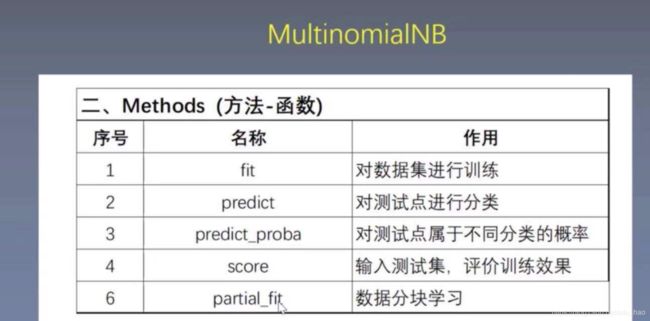
5. 试分别调用 sklearn.naive_bayes 的 GaussianNB、BernoulliNB、MultinomialNB 模块,对上述表格中训练数据进行分类。
之前碰到的都是特征是离散变量情形,如果特征是连续变量,如身高(如果训练集身高有175,177,如果把他当作离散变量来做,会有问题,比如预测时出现身高=176.5就没办法做了),此时要使用高斯分布。
"""
朴素贝叶斯算法sklearn实现
2019/4/15
"""
import numpy as np
from sklearn.naive_bayes import GaussianNB, BernoulliNB, MultinomialNB
from sklearn import preprocessing # 预处理
def main():
X_train = np.array([
[1, "S"],
[1, "M"],
[1, "M"],
[1, "S"],
[1, "S"],
[2, "S"],
[2, "M"],
[2, "M"],
[2, "L"],
[2, "L"],
[3, "L"],
[3, "M"],
[3, "M"],
[3, "L"],
[3, "L"]
])
y_train = np.array([-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1])
#对于离散型特征,我们要进行预处理 使每一个样本在每个特征上的取值为0或1
#比如第一个样本 的特征为1,S;其中第一个特征有三个取值 第二个特征也有三个取值
#转换后的特征为 1 0 0 0 0 1 (分别对应 1 2 3 L M S)
enc = preprocessing.OneHotEncoder(categories='auto')
enc.fit(X_train)
X_train = enc.transform(X_train).toarray()
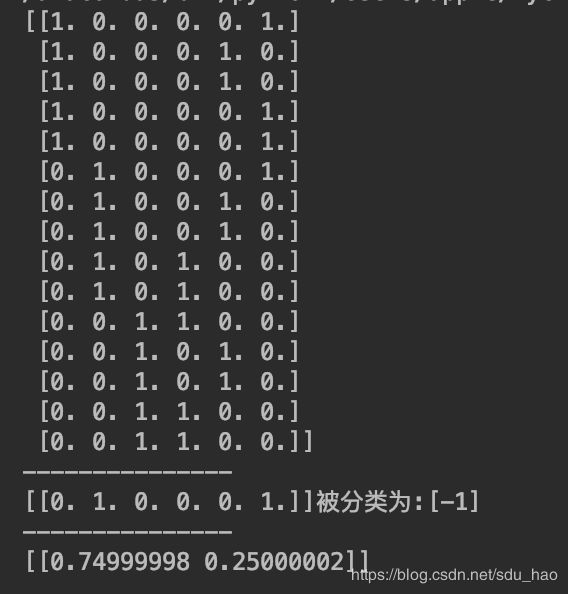
print(X_train)
print("---------------")
clf = MultinomialNB(alpha=0.0000001) #离散变量
clf.fit(X_train, y_train)
X_new = np.array([[2, "S"]]) #对预测样本也做相同的转换
X_new = enc.transform(X_new).toarray()
y_predict = clf.predict(X_new)
print("{}被分类为:{}".format(X_new, y_predict))
print("---------------")
print(clf.predict_proba(X_new)) #归一化概率
if __name__ == "__main__":
main()