AI学习笔记--skLearn--KMeans聚类
Scikit-learn(sklearn)的定位是通用机器学习库,而TensorFlow(tf)的定位主要是深度学习库。一个显而易见的不同:tf并未提供sklearn那种强大的特征工程,如维度压缩、特征选择等。究其根本,我认为是因为机器学习模型的两种不同的处理数据的方式:
-
传统机器学习:利用特征工程(feature engineering),人为对数据进行提炼清洗
-
深度学习:利用表示学习(representation learning),机器学习模型自身对数据进行提炼
Sklearn更倾向于使用者可以自行对数据进行处理,比如选择特征、压缩维度、转换格式,是传统机器学习库。而以tf为代表的深度学习库会自动从数据中抽取有效特征,而不需要人为的来做这件事情,因此并未提供类似的功能。
Scikit-Learn环境搭建
默认情况下,Scikit-Learn并非集成到TensorFlow环境中,如果需要使用,则需要使用pip下载。并且,scikit库包括几个分支,例如image处理的,scikit-image和scikit-learn两个库,在终端中输入一个命令即可解决:
➜ Python_Workplace pip install scikit-learn
Scikit-Learn 第一个程序
# -*- coding: utf-8 -*
from matplotlib import pyplot as plt
from sklearn.cluster import k_means
import pandas as pd
from sklearn.metrics import silhouette_score
file = pd.read_csv("cluster_data.csv", header=0)
x = file['x']
y = file['y’]
print file
第一个程序例子,我们了解一下Python的语法和执行环境。可以选用ipython作为编辑环境也可以使用编辑器sublime作为编写环境。编写代码: 上面的代码结构简单,导入sklearn的库,打开csv文件,并且采集数据,最后输出。这里有坑,可能会存在pandas mode找不到的情况,还有字符不对的情况。我们可以在py脚本上面添加相关编码格式、并且安装库的方式去解决这个问题。
➜ Python_Workplace pip install pandas
如果出现编码格式不对,在coding:下一行添加代码:
# -*- coding: utf-8 -*
import sys
reload(sys)
sys.setdefaultencoding('utf8')
如此一来,第一个sklearn学习demo代码就编写完成了,最后在终端执行脚本:
➜ Python_Workplace ipython k_means_cluster.py
接下来就可以看到对应的数据打印,CSV的逐条数据一一打印出来的情况了。
| x |
y |
| 0.0720376 |
0.221381067 |
| 0.058398649 |
0.24065473 |
| 0.064184457 |
0.229640274 |
| 0.076806009 |
0.230121658 |
| 0.073072657 |
0.235259831 |
| 0.07064053 |
0.229773075 |
| 0.048279513 |
0.270236579 |
| 0.049115359 |
0.245176393 |
| 0.043667391 |
0.255978852 |
| 0.063051153 |
0.250294758 |
| 0.054370789 |
0.264563296 |
| 0.0579757 |
0.278009583 |
| 0.037176407 |
0.260527888 |
| 0.074941076 |
0.262401247 |
| 0.040604012 |
0.263890693 |
这种数据不太好看,也可以用matplotlib工具把离散的点花在对应的坐标点上,编辑代码:
# -*- coding: utf-8 -*
from matplotlib import pyplot as plt
from sklearn.cluster import k_means
import pandas as pd
from sklearn.metrics import silhouette_score
file = pd.read_csv("cluster_data.csv", header=0)
x = file['x']
y = file['y']
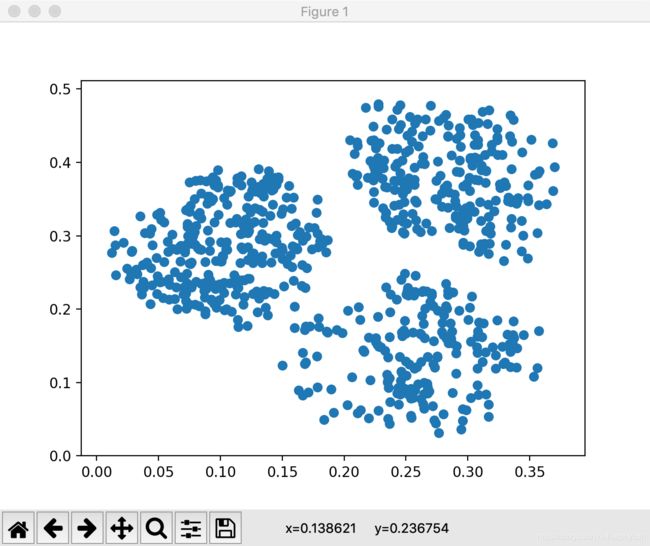
plt.scatter(x,y)
plt.show()
#print file
如此一来,就可以在GUI窗口上看到一个一个离散的点数据。
接下来学习一下聚类的方法,scikit-learn 关于聚类的算法都包括在了sklearn.cluster方法下面,我们使用k-Means方法来实现找中心。代码如下:
-*- coding: utf-8 -*
from matplotlib import pyplot as plt
from sklearn.cluster import k_means
import pandas as pd
from sklearn.metrics import silhouette_score
file = pd.read_csv("cluster_data.csv", header=0)
x = file['x']
y = file['y']
plt.scatter(x,y)
plt.show()
#from matplotlib import pyplot as plt
model = k_means(file,n_clusters = 3)
print model
#print file
执行脚本后,得到输出如下:
➜ Python_Workplace ipython k_means_cluster.py
(array([[0.26098231, 0.14011151],
[0.28288786, 0.37671499],
[0.1040997 , 0.28663691]]), array([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32), 3.349558811907321)
我们也可以用图形的方式来显示。添加代码:
# -*- coding: utf-8 -*
from matplotlib import pyplot as plt
from sklearn.cluster import k_means
import pandas as pd
from sklearn.metrics import silhouette_score
file = pd.read_csv("cluster_data.csv", header=0)
x = file['x']
y = file['y']
#plt.scatter(x,y)
#plt.show()
#from matplotlib import pyplot as plt
model = k_means(file,n_clusters = 3)
cluster_centers = model[0] # 聚类中心数组
cluster_labels = model[1] # 聚类标签数组
plt.scatter(x, y, c=cluster_labels) # 绘制样本并按聚类标签标注颜色
# 绘制聚类中心点,标记成五角星样式,以及红色边框
for center in cluster_centers:
plt.scatter(center[0], center[1], marker="p", edgecolors="red")
plt.show() # 显示图#print model
#print file
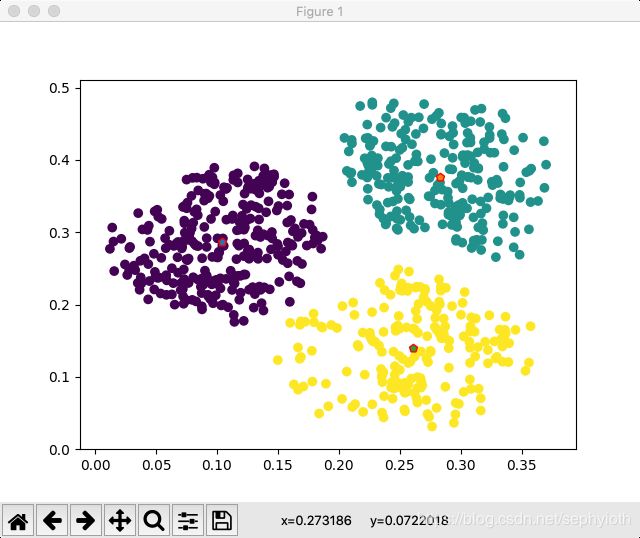
运行脚本,得到最终的输出图
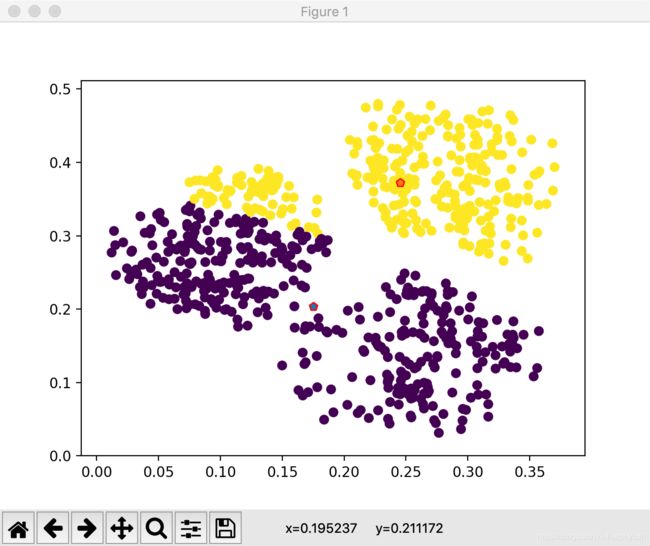
上图发现,数据类的中心位置,被标记位红圈,两边的数据都用紫色、蓝色、黄色等表示。k_Mean 可以看做是,找到一堆数据的集合,并且均值求得数据的中心。n_clusters则是对应的数据集合个数。如果调整这个参数为2个集群,得到的结果就不一样了。
那么,我们如何确定在K_mean 中K的数值?是否有方法去实现自动找。确定这个K有以下几个方法:
-
肘部法则
-
轮廓系数
-
肘部法则
肘部法则是一种启发性的学习算法,上面print 的时候,我们用到了前面三组数据,但是没用到最后一组,dtype这个参数,准确的来说,最后一组数据用来表示样本举例中心点的距离综合。可以想象,随着聚类采集的中心增大,相对应到中心点的距离也会逐渐减小,也就是说,如果样本只有一个类别的情况下,这个数值会逐渐变为0。可以通过曲线来表示数值和聚类数量之间的曲线关系。
编写测试代码:
# -*- coding: utf-8 -*
from matplotlib import pyplot as plt
from sklearn.cluster import k_means
import pandas as pd
from sklearn.metrics import silhouette_score
file = pd.read_csv("cluster_data.csv", header=0)
index = []
inertia = []
for i in range(9):
model = k_means(file,n_clusters = i + 1)
index.append(i+1)
inertia.append(model[2])
plt.plot(index,inertia,"-o")
plt.show()
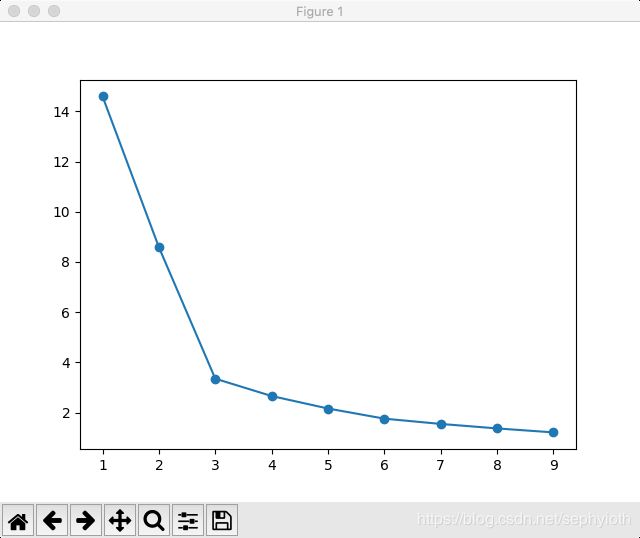
执行脚本后,可以发现对应的关系图如下:
这里有个明显的拐点,有点类似于关节肘部,是变化最大的情况,这里我们可以看到这个值明显是3左右,所以依据肘部原则,K阈值选择3。
-
轮廓系数
除了肘部原则,聚类还有一种评估方法,叫做轮廓系数。轮廓系数结合了聚类后的两项因素,内聚度和分离度。内聚度就指的是一个样本在集合中的不相似度,而分离度指的是一个样本在集合之间的不相似度。在scikit-learn中,同样提供了直接计算轮廓系数的方法。示例代码如下:
# -*- coding: utf-8 -*
from matplotlib import pyplot as plt
from sklearn.cluster import k_means
import pandas as pd
from sklearn.metrics import silhouette_score
file = pd.read_csv("cluster_data.csv", header=0)
index = []
#inertia = []
silhouette = []
for i in range(9):
model = k_means(file,n_clusters = i + 2)
index.append(i+2)
# inertia.append(model[2])
silhouette.append(silhouette_score(file,model[1]))
print silhouette
plt.plot(index,silhouette,"-o")
# plt.plot(index,inertia,"-o")
plt.show()
输出结果:
➜ Python_Workplace ipython k_means_cluster.py
[0.38937751658822506, 0.5614542787641772, 0.4834779533963621, 0.4381539507972644, 0.4071181742250774, 0.39122012638324916, 0.3836111661159799, 0.39710065914642656, 0.4028243567368712]
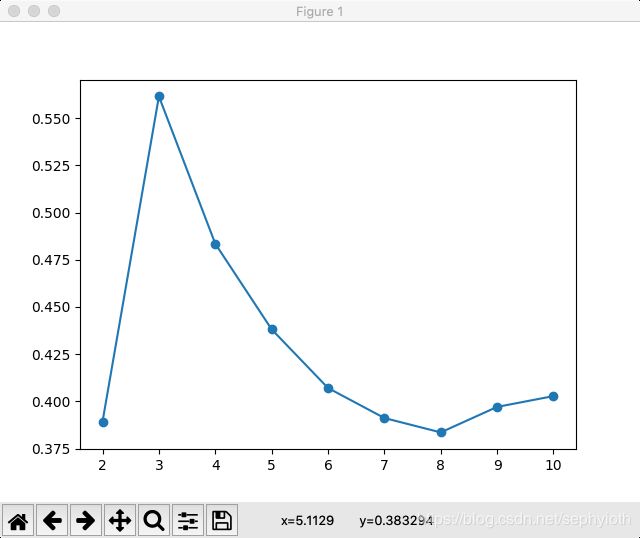
并且图:
轮廓系数的判别条件是,越接近1的状态,代表聚类的效果越好。从图上可以看出轮廓等于3的时候,效果最好。
-
Mini Batch K-Means
实现方法在sklearn.cluster.miniBatchKmeans方法中。
Min Batch K-Means整体效果和K-Means方法很相似,他是一种K-Means的变种形式。与K-Means不同的是,他每次都会从全部数据抽样小数据集进行迭代。Mini K-Means算法也会减少聚类的算法时间损耗。
-
Affinity Propagation
实现方法:sklearn.cluster.AffinityPropagation中。
Affinity Propagation又被称为亲和传播聚类。Affinity Propagation是基于数据点进行消息传递的理念设计。与K-Means聚类算法不同的点在于,他不需要提前确定聚类的数量,即K值,但是运行的效率较低。
-
Mean Shift
实现方法:sklearn.cluster.MeanShift
MeanShift 又被称为均值漂移聚类。Mean Shift 聚类的目的是找出最密集的区域, 同样 也是一个迭代过程。在聚类过程中,首先算出初始中心点的偏移均值,将该点移动到此偏 移均值,然后以此为新的起始点,继续移动,直到满足最终的条件。Mean Shift 也引入 了核函数,用于改善聚类效果。除此之外,Mean Shift 在图像分割,视频跟踪等领域也 有较好的应用。
-
Spectral Clustering
实现方法:sklearn.cluster.SpectralClustering
Spectral Clustering 又被称为谱聚类。谱聚类同样也是一种比较常见的聚类方法,它是从 图论中演化而来的。谱聚类一开始将特征空间中的点用边连接起来。其中,两个点距离越 远,那么边所对应的权值越低。同样,距离越近,那么边对应的权值越高。最后,通过对所有特征点组成的网络进行切分,让切分后的子图互相连接的边权重之和尽可能的低,而各子图内部边组成的权值和经可能高,从而达到聚类的效果。谱聚类的好处是能够识别任意形状的样本空间,并且可以得到全局最优解。
-
Agglomerative Clustering
实现方法:sklearn.cluster.AgglomerativeClustering
Agglomerative Clustering 又被称为层次聚类。层次聚类算法是将所有的样本点自下而 上合并组成一棵树的过程,它不再产生单一聚类,而是产生一个聚类层次。层次聚类通过 计算各样本数据之间的距离来确定它们的相似性关系,一般情况下,距离越小就代表相似度越高。最后,将相似度越高的样本归为一类,依次迭代,直到生成一棵树。由于层次聚 类涉及到循环计算,所以时间复杂度比较高,运行速度较慢。
-
Birch 聚类
实现方法:sklearn.cluster.Birch
Rirch 是英文 Balanced Iterative Reducing and Clustering Using Hierarchies 的简 称,它的中文译名为「基于层次方法的平衡迭代规约和聚类」。Birch 引入了聚类特征树(CF树),先通过其他的聚类方法将其聚类成小的簇,然后再在 簇间采用 CF 树对簇聚类。Birch 的优点是,只需要单次扫描数据集即可完成聚类,运行速度较快,特别适合大数据集。
-
DBSCAN
实现方法:sklearn.cluster.DBSCAN
DBSCAN 是英文 Density-based spatial clustering of applications with noise 的简 称,它的中文译名为「基于空间密度与噪声应用的聚类方法」。DBSCAN 基于密度概念,要求聚类空间中的一定区域内所包含的样本数目不小于某一给 定阈值。算法运行速度快,且能够有效处理特征空间中存在的噪声点。但是对于密度分布 不均匀的样本集合,DBSCAN 的表现较差。
-
算法对比
算法需要一个新的数据文件。代码和大致数据如下:
数据:
x y class
5.867498067 8.17715188 0
5.613699815 9.932955266 0
7.225084278 10.44886194 0
6.762822546 0.605145352 1
8.0161824 1.543147009 1
8.40185356 -0.373481315 1
6.511922767 9.81342902 0
7.399679603 0.91258881 1
-4.984363346 -11.42227525 2
9.888250958 0.902413919 1
8.80002143 8.543235209 0
7.95311372 8.368976645 0
6.108460663 8.233439954 0
8.339755138 8.888149572 0
8.88361084 9.01589874 0
脚本代码:
# -*- coding: utf-8 -*
from matplotlib import pyplot as plt
from sklearn import cluster
import pandas as pd
import numpy as np
from sklearn.metrics import silhouette_score
data = pd.read_csv("data_blobs.csv", header=0)
x = data[['x', 'y']]
y = data['class']
plot_num = 1 # 为绘制子图准备
cluster_names = ['KMeans', 'MiniBatchKMeans', 'AffinityPropagation', 'MeanShift', 'Sp ectralClustering', 'AgglomerativeClustering', 'Birch', 'DBSCAN']
# 确定聚类方法相应参数
cluster_estimators = [
cluster.KMeans(n_clusters=3),
cluster.MiniBatchKMeans(n_clusters=3),
cluster.AffinityPropagation(),
cluster.MeanShift(),
cluster.SpectralClustering(n_clusters=3),
cluster.AgglomerativeClustering(n_clusters=3),
cluster.Birch(n_clusters=3),
cluster.DBSCAN()
]
for name, algorithm in zip(cluster_names, cluster_estimators):
algorithm.fit(x) # 聚类
# 判断方法中是否由 labels_ 参数,并执行不同的命令
if hasattr(algorithm, 'labels_'):
algorithm.labels_.astype(np.int)
else:
algorithm.predict(x)
# 绘制子图
plt.subplot(2, len(cluster_estimators) / 2, plot_num)
plt.scatter(data['x'], data['y'], c=algorithm.labels_)
# 判断方法中是否由 cluster_centers_ 参数,并执行不同的命令
if hasattr(algorithm, 'cluster_centers_'):
centers = algorithm.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], marker="p", edgecolors="red")
# 绘制图标题
plt.title(name)
plot_num += 1
plt.show()
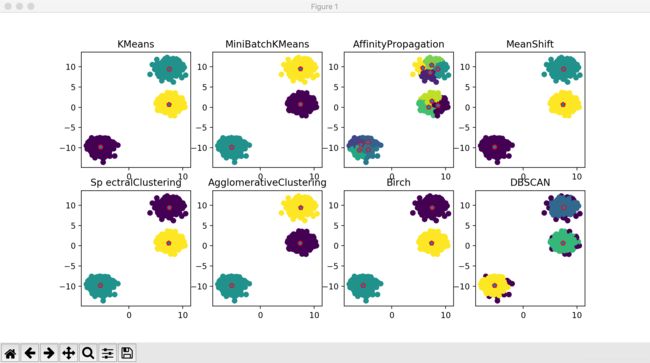
最后,参照各类方法锁输出的结果如下图:
By Genesis.Ling