电梯调度
在像芝加哥,纽约,东京,新加坡,香港等大城市里,每天都会有上百万的人通过电梯离开他们的大楼。但是我们却很少考虑电梯是如何调度来提供服务的,尤其是在人流高峰期,这个时候办公楼里的大多数人都会企图在大约一个小时左右离开。
关于这方面主题(基于乘客等待时间的电梯分配系统)和研究(电梯流量模拟)的算法至少有一个专利,并且出现在Quaro上。曾经在一次面试中,面试官问我我会如何调度电梯。这点我之前有提到过:
“ 假如有十层楼,每层都有相同数量的人,一共有三部电梯并且没有楼梯。你将如何分配电梯来实现性能最优,及最小化每一层的等待时间?”
我很喜欢这个面试问题。我觉得这个问题很有挑战性而且你可以想得尽量深入,但是也应该足够直接以便于你下手,产生某些解决方案。没有绞尽脑汁想一个月来模拟真实场景,在这篇文章中,我会尝试解决一个简化的电梯调度问题,类似于上面的面试问题。
问题描述
创造一个可用于现实生活中电梯运行的算法(很显然,这类算法已被申请专利)是有难度的。因此,我会努力解决一些与我面试问题类似的问题,我会做一点轻微变换:
设计一个使大楼里所有人等待时间最短的算法,同时要考虑每一层的负载量。假定每一层人数相同且每层的人以同样的方式使用电梯。假设每天有几个小时是“高峰时段”,算法需要提供一种最“公平”的方式来将电梯分配到不同的楼层。
上面是对问题的整体描述,但是如果我们将问题分解,该问题包含以下条件:
- 楼层数量任意
- 电梯数量任意
- 给定高峰时段
- 我们必须通过某种关于负载和时间的函数来分配电梯
一些我们需要考虑但是未说明的变量或者常量:
- 每层人数:100人
- 电梯通过一层的时间(不停):5秒钟
- 每层的等待时间:20秒钟
我给上面的变量赋值,而且尽管“电梯通过每一层的时间”有可能不是线性的(即电梯需要花时间从停止位置开始加速),但是我们还是这样假设。虽然做这些假设可能会“过度简化”问题,但是我相信这篇文章已经可以满足面试要求而且可以作为一个很好的契入点,来引发更深的思考和讨论。
注意,我并没有考虑电梯的容量,在这方面我要做个很大胆的假设。我的假设(贯穿整个方案)是每个电梯的容量无限大。很显然这是不正确的,但是一旦我们有了解决方案,我认为增加像这样的声明会容易得多:
如果电梯满了,回到较下的楼层;释放乘客后再返回原来的楼层。
我可能会另外写一篇文章放到这个博客里,或者我会通过我的邮件列表来发布。不管哪种情况,我希望有人能想办法自己来解决!
电梯分配算法
这可能不是最佳方案,尽管它有可能效果不错。你如果找到一个更好的方案,请分享!
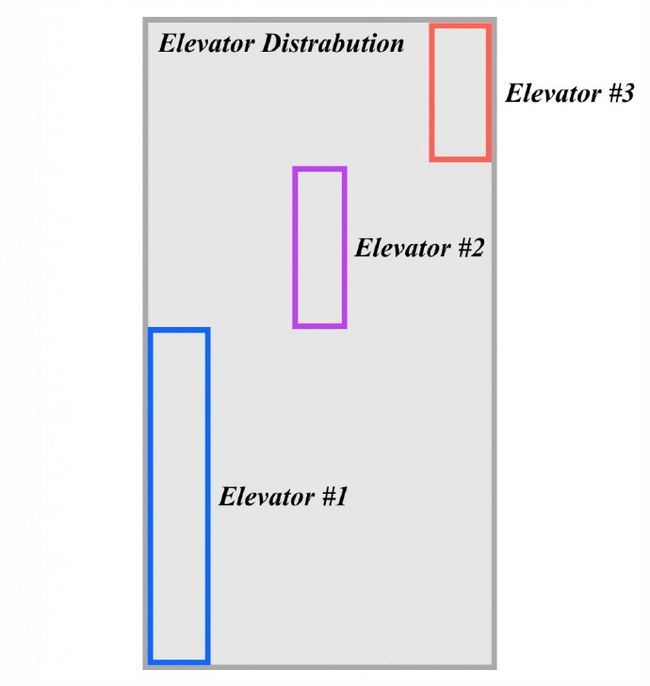
正如上面图片显示的,我会给特定的楼层指定 一个具体的电梯,我称之为区域电梯分配。这个想法在于我们可以获得每层的平均等待时间和每层的平均负载量。
我的这个特殊方法是基于我对每个电梯形成一个回路(即在电梯循环里经过所有楼层,例如:0->1->2->0)所花费时间的一些观察。我们所有要知道的就是下面这些,来计算一个电梯完成一次回路所需的时间:
- 经过一层楼的时间乘以往返中最高楼层数乘以2(上和下),在我们问题中:(5 seconds *
* 2) - 从最低楼层到最高楼层之间电梯停的层数乘以每次停等所花费的时间,在我们问题中:(20 seconds *
)
总的往返时间:
elevatorsCircuitTime = (5*
使用下面方程计算一个往返中电梯的平均载人数:
avgElevatorLoad =
变量 rushHour等于完成运输一个高峰时间段所花费时间,floorsServiced等于电梯所停的楼层数,peoplePerFloor指给定楼层的人数。因为我们已经计算出了电梯往返时间,所以我们可以利用这个时间和平均负载性能来实现我们的算法。
我给这个问题的解决方案需要两个数组:
大楼的表示:大楼数组中每个元素代表每层的人数。数组的每个单元表示一层楼。例如[100 100 100]可以表示一栋四层楼,只有高三层的人需要使用电梯。
电梯的表示:电梯数组中的每个单元代表该电梯在它回路中所能到达的最高层(为了简化我把0放进第0个单元)。例如,[0,2,3]表示两个电梯,1号电梯(在1号单元)运载乘客从2楼到1楼到0,2号电梯(在2号单元)运载乘客从3楼到0。
初始时,1号数组(表示大楼)为空,然后每次我给该数组“增加一层”时,我给这一层分配一个电梯。如你所见,这种分配是可以改变的,但是它会遵从一个相似的形式。拥有最小往返的电梯回路会被分配该新的楼层,除非需要涉及性能问题。我增加了一个小方程:
elevatorCircuitTime + ((elevatorCircuitTime / 100) * elevatorsAvgLoad)
因为elevatorCircuitTime 是一个整数,除非往返时间超过100秒(这对电梯来说是一个很长的时间),将elevatorsAvgLoad乘到这个方程中。我们的问题描述非常模糊,而且考虑到上面的方程,我的解决方案同样地的确有一些模糊之处。同样地,我用来分配楼层给电梯的函数十分任意,但是在负载管理中却十分有效(尽管可能会有更好的方案)。
下面是层架楼层函数的实现代码:
# (Index * 5 seconds) + (20 seconds * (Index - PrevIndex))
# If previous elevators loops/stops add up to be greater than,
# (timePerFloor * 2) + timePerWait, then increase floor of previous
# elevators loop. i.e. elevator[2]+=1
# e represents elevatorArray
def addFloor(e):
best = 99999
for i in range(1, len(e)):
cirTime, avgCarry = eleLoop(e, i)
if cirTime + ((cirTime / 100) * avgCarry) < best:
elevatorNumber = i
best = cirTime + ((cirTime / 100) * avgCarry)
for i in range(elevatorNumber, len(e)):
e[i] += 1
return e注意,每次一个 “elevatorNumber”被选择后,所有在 “elevatorNumber”之上的电梯所到达的最高楼层数加1:
for i in range(elevatorNumber, len(e)):
e[i] += 1
这是因为在被选择之上的每个电梯往返所到达的最高的楼层会加1,但是我们只希望增加一个额外的电梯到被选择的电梯回路中。附加函数eleLoop(e, i)很容易确定在被选择回路中的往返时间和平均载客量。
一旦我们有了增加楼层的函数,我就可以构造函数来循环通过和创建楼层。注意,在本情况中,所有楼层被设定为统一的。这样如果本问题被扩展为每层人数不同的情况,也会相对容易考虑。
# Allocate elevators
# Elevator[] represents the starting
# group of stops.
def elevatorAllocation(building, elevatorCount):
elevator = []
for i in range(elevatorCount + 1):
elevator.append(0)
for i in range(1, floorCount):
elevator = addFloor(elevator)
printeleLoop(elevator)以上便是算法分配部分的大体。本算法相对直接而且留有一定量的的改进空间,我将这部分留给大家来解决!
实现|Python语言
如果将算法的各部分拼接起来,再加一些额外的函数来打印数据,创建一个小巧的模拟器,我们就可以获得一个很酷的小程序(大家可以从我的github中fork下来或者查看)。
变量:
- 10层楼
- 3部电梯
- 1个高峰时段
- 通过一层耗时5秒
- 电梯需要停等时,每次停20秒
- 每层100人
# Sets up the building, filling all the floors with people def fillBuilding(): building = [] for i in range(floorCount - 1): building.append(peoplePerFloor) return building # Determines the time for circuit (cirTime), # as well as average carrying capacity per circuit. # Given e - array of elevators, which holds the highest # serviced floor, and i the current index of e. def eleLoop(e, i): floorsServiced = e[i] - e[i-1] + 1 cirTime = timePerFloor * e[i] * 2 cirTime += timePerWait * floorsServiced avgCarry = cirTime * peoplePerFloor / rushHour * floorsServiced return cirTime, avgCarry # (Index * 5 seconds) + (20 seconds * (Index - PrevIndex)) # If previous elevators loops/stops add up to be greater than, # (timePerFloor * 2) + timePerWait, then increase floor of previous # elevators loop. i.e. elevator[2]+=1 def addFloor(e): best = 9999 for i in range(1, len(e)): cirTime, avgCarry = eleLoop(e, i) if cirTime + ((cirTime / 100) * avgCarry) < best: elevatorNumber = i best = cirTime + ((cirTime / 100) * avgCarry) for i in range(elevatorNumber, len(e)): e[i] += 1 return e # Prints the population of the buildings floor as an array. def printApprox(building): str = '[ ' for i in range(len(building)): str += '%06.3f ' % building[i] str += ']' print str # Prints the circuit(s) for each of the elevators def printeleLoop(e): print '' print e print '' for i in range(1, len(e)): floorsServiced = e[i] - e[i-1] + 1 curr = timePerFloor * e[i] * 2 curr += timePerWait * floorsServiced avgCarry = curr * peoplePerFloor / rushHour * floorsServiced str = 'Elevator #%d, time for loop %d seconds, ' % (i, curr) str += 'carrying an average of ' str += '%3.2f people per carry' % avgCarry print str print '' # Allocate elevators # Elevator[] represents the starting # group of stops. def elevatorAllocation(building, elevatorCount): elevator = [] for i in range(elevatorCount + 1): elevator.append(0) for i in range(1, floorCount): elevator = addFloor(elevator) printeleLoop(elevator) return elevator # Simulates the building being emptied at rush hour def simulate(e, building): str = '[ ' for floor in range(len(building)): str += 'floor%2d ' % (floor + 1) str += ']' print str eCircuit = [] for i in range(len(e)): curr, avgCarry = eleLoop(e, i) eCircuit.append(float(curr)) emptyFloors = 0 iteration = 0 finalFloor = 0 while emptyFloors < len(building): emptyFloors = 0 iteration += 1 for i in range(1, len(e)): for j in range(e[i-1], e[i]): if building[j] > 0.0: persons = eCircuit[i] * peoplePerFloor / rushHour building[j] = building[j] - persons if 0 >= building[j]: building[j] = 0.0 emptyFloors += 1 finalFloor = j printApprox(building) print '' # Find the final elevator on circuit, prints time for i in range(len(e)): if e[i] > finalFloor: iteration = eCircuit[i] * iteration / 60 print 'Total Time: %d minutes\n' % (iteration) # ___ MAIN ____ building = fillBuilding() elevator = elevatorAllocation(building, elevatorCount) simulate(elevator, building)
输出:
[0, 4, 7, 9]
- #1电梯:往返用时140秒,平均每次载客19.44人
- #2电梯:往返用时150秒,平均每次载客16.67人
- #3电梯:往返用时150秒,平均每次载客12.50人
总用时:65分钟
电梯往返时,每层的平均人数变化情况:
如你所见,我的算法提供了一个良好的但不是最佳的方案(在本情况下)。本算法虽然还有很大的改进空间(我将这部分留给你们来挑战),但是它是一个好的开始。
计算运行时
计算本算法的时间和空间要求会有一点难度,但也不是很难。算法的运行时取决于以下三个因素:
- k:最大回路,人数
- n:在最大回路中需要服务楼层的起始人数
- m:总的楼层数
(1)运行时:O(m * (n/k))
‘n / k’ :决定了电梯需要的最大往返次数;‘m’ :这一项是因为在电梯往返过程中需要对每一层进行迭代。在本情况中,我们忽略了初始化大楼数组这一步骤,该数组代表每一层的人数,因为这一项不是运行时(m*(n/k) + m)的主要项。
最大空间需求很直接:
- e:电梯数量
- f:楼层数量
(2)内存要求:O(e + f)
将以上因素整合起来:
- k:最大回路,人数
- n:在最大回路中需要服务楼层的起始人数
- m:总的楼层数
- e:电梯数量
- f:楼层数量
- 运行时间:O(m * (n / k))
- 内存要求:O(e + f)
结束语
我认识到这并不是一个最佳方案,然而它确实解决了问题。我挑战你们来进行评论,从我的github中fork,改进我的代码或者是在自己的文章中写下自己的方案。我认为这是一个很有趣的问题,而且同你们电脑内部的资源分配类似,我还写了篇基本的调度处理导论的文章,如果你们感兴趣,可以来读一读。我同样十分乐意看到一个不同的(希望更好的)方案,所以如果你们想到了更好的方案,一定不要忘记写下来。
我本来确实打算另写一篇文章来更深地挖掘这个问题,并提供一个更接近现实世界应用的算法,但是我还没有确定日期(可能是几天,几周或者是几个月)。我希望你们喜欢这篇文章而且我也很乐意听听你们的想法,所以不要犹豫是否评论和跟我发邮件,谢谢!