后缀自动机 (suffix automaton, SAM) 是一个能解决许多字符串相关问题的有力的数据结构。(否则我们也不会用它)
举几个例子,以下的字符串问题都可以在线性时间内通过 SAM 解决
1.在另一个字符串中搜索一个字符串的所有出现位置。(诶?KMP好像能做)
2.计算给定的字符串中有多少个不同的子串。(诶?好像也能做)
3.统计一个子串所有不同子串的总长度 (额,线性复杂度?以前的知识好像就不行了)
4.字典序第k大/小子串(字典树好像可以做,但线性?不会!)
5.给定一个字符串 。找出字典序最小的循环移位。(这个我会!最小表示法!)
6.对于一个给定的文本串T ,有多组询问,每组询问给一个模式串S ,回答模式串S在字符串T中作为子串出现了多少次。(AC自动机!也可以)
7.给定一个字符串S 和一个特定的字符集,我们要找一个长度最短的没有在S中出现过的字符串。(以前的知识做不到我太菜了)
8.两个字符串的最长公共子串(线性??!以前的知识做不到我太菜了)
9.多个字符串的最长公共子串(我不会!!)
这么多东西都可以线性时间内解决,厉害吧;
厉害的前提是你先要学会后缀自动机
接下来进入正题:
SAM是什么?
1.SAM 是一张有向无环图。结点被称作 状态 ,边被称作状态间的 转移 。
2.图存在一个源点root称作 初始状态 ,其它各结点均可从root出发到达。每个 转移 都标有一些字母。从一个结点出发的所有转移均 不同 。
3.存在一个或多个 终止状态 。如果我们从初始状态出发,最终转移到了一个终止状态,则路径上的所有转移连接起来一定是字符串S的一个后缀。
4.S的每个后缀均可用一条从到某个终止状态的路径构成。
5.在所有满足上述条件的自动机中,SAM 的结点数是最少的。
具体可以证明,SAM的点数最多是2*n-1,边数最多时3*n-4; (暂时为了方便理解并不证明,你只要露出"哇!这是上限吗","我靠,这SAM的复杂度也太***的强了"的表情就好了);
SAM的性质:
SAM 最简单、也最重要的性质是,它包含关于字符串的所有子串的信息。任意从初始状态开始的路径,如果我们将转移路径上的标号写下来,都会形成S的一个子串 。反之每个S的子串对应从初始状态开始的某条路径。
为了更好的理解SAM(背模板,水经验),我们定义一些奇怪的东西;(不要一看到不认识的概念就跳过去,否则建图会看不懂的)
1.endpos等价类
考虑字符串S的任意非空子串t,我们记endpos(t)为在字符串S中t的所有结束位置.
让我们举个栗子:(假设对字符串中字符的编号从零开始)
对于S=“cbacbaba” endpos(ba)="2,5,7" endpos(a)="2,5,7" endpos(cba)="2,5";
我们发现,对于"ba"和"a"的endpos等价类的数值是完全相同的,那么这对与SAM来说是个好东西,我们可以将所有endpos相同的子串放到SAM的一个节点上,大大节省了空间与时间复杂度;
那么一个重要的结论出现了:SAM上的每个节点都代表一个endpos等价类;(比如刚才的栗子中,子串"ba","a"在SAM上用一个节点表示)
我们发现一个不是引理的性质:对于一个子串S,不断的删除它开头的元素,那么它的endpos一定是在已有的旧元素基础上加入一些新元素(或者不加),大致理解一下对于下面的引理很好理解
引理1:字符串S的两个非空子串x和y的endpos相同,当且仅当字符串x在S中的每次出现,都是以y后缀的形式存在的。(x<=y) (很显然的对吧?)
引理2:两个非空子串x,y, 他们的endpos的不可能存在交集 (很显然的对吧)
引理3:考虑一个endpos等价类,将类中的所有子串按长度递减的顺序排序。每个子串是它前一个子串的后缀。
换句话说,对于同一等价类的任一两子串,较短者为较长者的后缀,且该等价类中的子串长度恰好覆盖整个区间;
粗略证明感性理解:对于一个endpos等价类中的最长子串x,和最短子串y,若y的开头加一个元素,使得新形成的字符串z是S的子串,那么如果z的长度<=x,则endpos(z)
一定=endpos(y)=endpos(x); 使用数学归纳法可以证明所有的y<=z<=x;z的endpos都与x,y相同;
2.后缀链接 link:
考虑 SAM 中某个不是root的一个状态 。我们已经知道,状态v对应于具有相同endpos的等价类。我们如果定义x为这些字符串中最长的一个,则所有其它的字符串都是x的后缀。
一个后缀链接link连接到对应于状态v的最短子串的所有后缀中长度最大的那个endpos等价类。
引理1:所有后缀链接构成一棵根节点为root的树 (和造一颗随机树的原理相同:对于一个endpos等价类v,只会连到比v的最短子串小的endpos等价类)
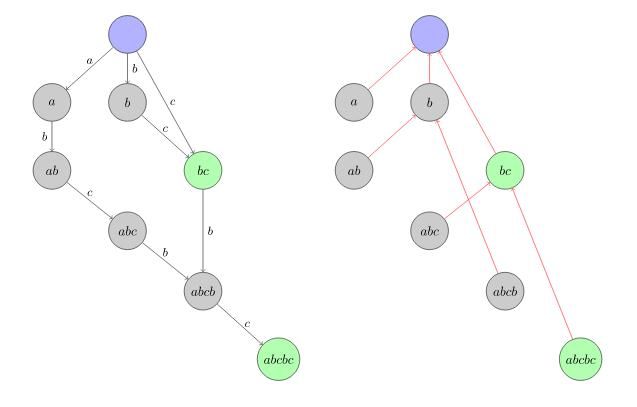
下面放两张图:对于字符串"abcbc",前者是表示边的转移状态,后者表示link的连接方式;
好了,定义暂时告一段落了;接下来就是构造环节了(代码):(别人家的构造过程 (逃~)
!!极度建议结合之前的定义来阅读!!
代码实现就是:
class node{
public:
int ch[28];
int link;
int len;
}SAM[3000010];
int ans[3000010];
int last=0,size=1;
void SAM_build()
{
SAM[0].len=0;
n=strlen(s+1);
SAM[0].link=-1;
inc(u,1,n){
int c=s[u]-'a';
int cur=size++;
ans[cur]=1;
SAM[cur].len=SAM[last].len+1;
int p=last;
while(p!=-1&&!SAM[p].ch[c]){
SAM[p].ch[c]=cur;
p=SAM[p].link;
}
if(p==-1){
SAM[cur].link=0;
}
else{
int q=SAM[p].ch[c];
if(SAM[q].len==SAM[p].len+1){
SAM[cur].link=q;
}
else{
int newq=size++;
SAM[newq]=SAM[q];
SAM[newq].len=SAM[p].len+1;
while(p!=-1&&SAM[p].ch[c]==q){
SAM[p].ch[c]=newq;
p=SAM[p].link;
}
SAM[q].link=newq;
SAM[cur].link=newq;
}
}
last=cur;
}
}