理解支持向量机（二）核函数

由之前对核函数的定义（见统计学习方法定义7.6）：
设χ是输入空间（欧氏空间或离散集合），Η为特征空间（希尔伯特空间），如果存在一个从χ到Η的映射

φ(x): χ→Η

使得对所有的x,z∈χ,函数Κ(x,z)=φ(x)∙φ(z)，
则称Κ(x,z)为核函数，φ(x)为映射函数，φ(x)∙φ(z)为x,z映射到特征空间上的内积。
由于映射函数十分复杂难以计算，在实际中，通常都是使用核函数来求解内积，计算复杂度并没有增加，映射函数仅仅作为一种逻辑映射，表征着输入空间到特征空间的映射关系。例如：
设输入空间χ： ,

映射函数φ(x)= < X,X > =
核函数Κ(x,z)=
那么，取两个样例x=(1,2,3),z=(4,5,6)分别通过映射函数和核函数计算内积过程如下：
φ(x)=(1,2,3,2,4,6,3,6,9)
φ(z)=(16,20,24,20,25,30,24,30,36)
φ(x)∙φ(z)=16+40+72+40+100+180+72+180+324=1024
而直接通过Κ(x,z)计算得[(4+10+18)]^2=1024
两者相比，核函数的计算量显然要比映射函数小太多了。

从上可知，如果我们知道核函数的话，那么就可以在不增加计算复杂度的情况下完成非线性变换。那么我们下一步的任务就是确定核函数。
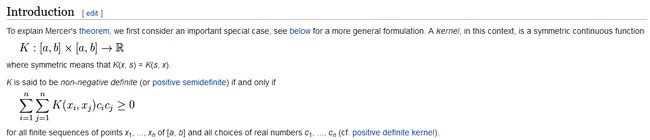
通常我们所说的核函数就是正定核函数，什么函数是正定核函数呢？
这里给出判定正定核的充要条件（见统计学习方法定理7.5）：
设Κ：χ×χ→R是对称函数，则Κ(x,z)为正定核函数的充要条件是对任意x_i∈χ,i=1,2,…,m,Κ(x,z)对应的Gram矩阵：

是半正定矩阵。
由充要条件可以给出判定正定核的等价定义：
设χ为输入空间，Κ(x,z)是定义在χ×χ对称函数，如果对任意x_i∈χ,i=1,2,…,m,Κ(x,z)对应的Gram矩阵：

是半正定矩阵，则称Κ(x,z)是正定核。
符合这样条件的函数，我们称它为正定核函数。
但值得提下的是，该定义是判定正定核的，也存在核函数是非正定核的，，如多元二次核函数：

在实际应用中，我们会经常用到Mercer定理还确定核函数。由Mercer定理得到的核函数称为Mercer核，正定核与Mercer核的维基百科定义分别如下：

由以上定义可以看出，正定核比Mercer核更具有一般性，因为正定核要求函数为定义空间上的对称函数，而Mercer核要求函数为对称连续函数。

二、常用核函数
1、线性核函数
线性核函数是最简单的核函数，是径向基核函数的一个特例，公式为：

主要用于线性可分的情形，对应上一篇讲的线性可分支持向量机与线性支持向量机。它在原始空间中寻找最优线性分类器，具有参数少速度快的优势。
2、多项式核函数
多项式核适合于正交归一化（向量正交且模为1）数据，公式为：

多项式核函数属于全局核函数，允许相距很远的数据点对核函数的值有影响。参数d越大，映射的维度越高，计算量就会越大。当d过大时，由于学习复杂性也会过高，易出现“过拟合现象。
3、径向基核函数&高斯核函数
径向基核函数属于局部核函数，当数据点距离中心点变远时，取值会变小。公式为：

高斯核函数可以看作是径向基核函数的另一种形式：

高斯径向基核对数据中存在的噪声有着较好的抗干扰能力，由于其很强的局部性，其参数决定了函数作用范围，随着参数σ的增大而减弱。
4、Sigmoid核函数
Sigmoid核函数来源于神经网络，被广泛用于深度学习和机器学习中。公式为：

采用Sigmoid函数作为核函数时，支持向量机实现的就是一种多层感知器神经网络。支持向量机的理论基础（凸二次规划）决定了它最终求得的为全局最优值而不是局部最优值，也保证了它对未知样本的良好泛化能力。
5、字符串核函数
核函数不仅可以定义在欧氏空间上，还可以定义在离散数据的集合上。字符串核函数是定义在字符串集合上的核函数，可以直观地理解为度量一对字符串的相似度，在文本分类、信息检索等方面都有应用。