python 非线性规划(scipy.optimize.minimize)
一.背景:现在项目上有一个用python 实现非线性规划的需求。非线性规划可以简单分两种,目标函数为凸函数 or 非凸函数。
凸函数的 非线性规划,比如fun=x^2+y^2+x*y,有很多常用的python库来完成,网上也有很多资料,比如CVXPY
非凸函数的 非线性规划(求极值),从处理方法来说,可以尝试以下几种:
1.纯数学方法,求导求极值;
2.使用神经网络,深度学习来处理,可参考反向传播算法中链式求导的过程;
3.寻找一些python库来做,本文介绍scipy.optimize.minimize的使用方法
二.库方法介绍
官方文档:https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
来看下改方法的入参
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
解释:
fun: 求最小值的目标函数
x0:变量的初始猜测值,如果有多个变量,需要给每个变量一个初始猜测值。minimize是局部最优的解法,所以
args:常数值,后面demo会讲解,fun中没有数字,都以变量的形式表示,对于常数项,需要在这里给值
method:求极值的方法,官方文档给了很多种。一般使用默认。每种方法我理解是计算误差,反向传播的方式不同而已,这块有很大理论研究空间
constraints:约束条件,针对fun中为参数的部分进行约束限制
三.demo
1.计算 1/x+x 的最小值
# coding=utf-8
from scipy.optimize import minimize
import numpy as np
#demo 1
#计算 1/x+x 的最小值
def fun(args):
a=args
v=lambda x:a/x[0] +x[0]
return v
if __name__ == "__main__":
args = (1) #a
x0 = np.asarray((2)) # 初始猜测值
res = minimize(fun(args), x0, method='SLSQP')
print(res.fun)
print(res.success)
print(res.x)执行结果:函数的最小值为2点多,可以看出minimize求的局部最优
2.计算 (2+x1)/(1+x2) - 3*x1+4*x3 的最小值 x1,x2,x3的范围都在0.1到0.9 之间
# coding=utf-8
from scipy.optimize import minimize
import numpy as np
# demo 2
#计算 (2+x1)/(1+x2) - 3*x1+4*x3 的最小值 x1,x2,x3的范围都在0.1到0.9 之间
def fun(args):
a,b,c,d=args
v=lambda x: (a+x[0])/(b+x[1]) -c*x[0]+d*x[2]
return v
def con(args):
# 约束条件 分为eq 和ineq
#eq表示 函数结果等于0 ; ineq 表示 表达式大于等于0
x1min, x1max, x2min, x2max,x3min,x3max = args
cons = ({'type': 'ineq', 'fun': lambda x: x[0] - x1min},\
{'type': 'ineq', 'fun': lambda x: -x[0] + x1max},\
{'type': 'ineq', 'fun': lambda x: x[1] - x2min},\
{'type': 'ineq', 'fun': lambda x: -x[1] + x2max},\
{'type': 'ineq', 'fun': lambda x: x[2] - x3min},\
{'type': 'ineq', 'fun': lambda x: -x[2] + x3max})
return cons
if __name__ == "__main__":
#定义常量值
args = (2,1,3,4) #a,b,c,d
#设置参数范围/约束条件
args1 = (0.1,0.9,0.1, 0.9,0.1,0.9) #x1min, x1max, x2min, x2max
cons = con(args1)
#设置初始猜测值
x0 = np.asarray((0.5,0.5,0.5))
res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
print(res.fun)
print(res.success)
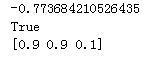
print(res.x)执行结果:
对于这种简单的函数,可以看出局部最优的求解和真实最优解相差不大,对于复杂的函数,x0的初始值设置,会很大程度影响最优解的结果。
ADD:
全局最优的函数: scipy.optimize.basinhopping
有一个缺点是无法设置约束,求全局的最优解的函数
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.basinhopping.html