K-means和PAM聚类算法Python实现及对比

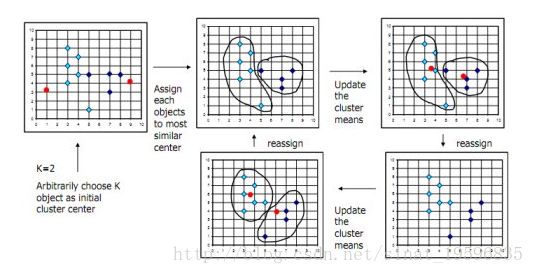
K-means（K均值划分）聚类：简单的说，一般流程如下：先随机选取k个点，将每个点分配给它们，得到最初的k个分类；在每个分类中计算均值，将点重新分配，划归到最近的中心点；重复上述步骤直到点的划归不再改变。下图是K-means方法的示意。

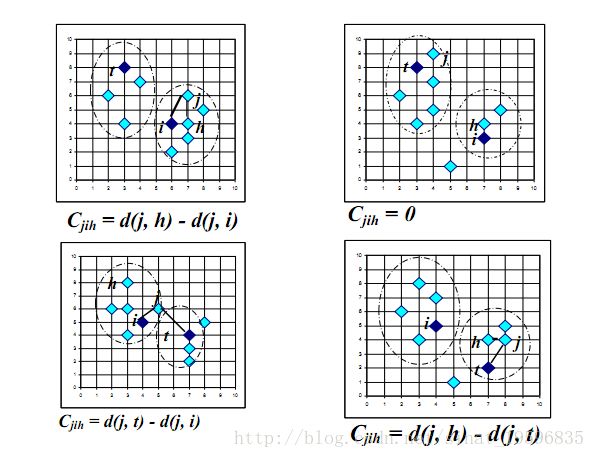
PAM（Partition Around Medoids）是K-medoid（K中心点划分）的基础算法，基本流程如下：首先随机选择k个对象作为中心，把每个对象分配给离它最近的中心。然后随机地选择一个非中心对象替换中心对象，计算分配后的距离改进量。聚类的过程就是不断迭代，进行中心对象和非中心对象的反复替换过程，直到目标函数不再有改进为止。非中心点和中心点替换的具体类别如下图分析（用h替换i相对j的开销）。

数据集：N=300，K=15

9.802   10.132
10.35   9.768
10.098  9.988
9.73    9.91
9.754   10.43
9.836   9.902
10.238  9.866
9.53    9.862
10.154  9.82
9.336   10.456
9.378   10.21
9.712   10.264
9.638   10.208
9.518   9.956
10.236  9.91
9.4 10.086
10.196  9.746
10.138  9.828
10.062  10.26
10.394  9.984
10.284  10.348
9.706   9.978
9.906   10.588
10.356  9.198
9.954   9.704
9.796   10.378
10.386  10.608
10.41   9.912
10.172  10.598
10.286  9.712
9.932   10.234
10.298  9.948
10.352  9.932
9.848   10.328
10.514  10.498
9.944   9.934
9.92    10.022
9.908   10.606
10.182  9.99
10.256  9.25
12.04   10.028
12.082  10.044
12.4    10.156
11.988  9.926
12.34   9.918
12.228  9.978
12.348  10.488
12.044  9.358
11.736  10.122
12.35   9.798
11.246  10.122
12.276  10.99
12.374  10.018
12.53   10
12.27   9.792
12.364  10.176
12.458  10.18
11.952  9.682
11.772  9.924
11.502  10.008
12.134  9.482
11.628  10.286
12.064  9.616
11.906  9.82
11.736  10.29
12.114  10.904
11.59   9.712
12.648  9.814
12.164  11.018
12.22   9.796
11.846  9.634
11.808  10.058
12.096  9.846
11.594  10.078
12.252  9.938
11.998  9.676
11.894  10.012
12.274  9.936
12.176  10.364
12.104  10.388
11.372  11.466
10.94   11.482
11.084  11.554
11.232  11.374
11.22   11.64
10.962  11.75
11.014  11.746
11.524  10.982
11.012  11.364
11.2    11.062
11.626  11.894
11.23   11.728
11.144  11.91
11.106  11.868
11.53   11.918
11.21   11.114
10.746  11.702
11.154  11.692
11.412  11.924
10.948  11.532
10.988  12.298
10.96   11.392
11.656  11.346
11.178  12.062
11.368  11.56
11.264  11.724
11.554  11.576
10.974  11.114
11.12   11.634
11.51   12.052
10.95   11.402
11.864  12.406
11.198  10.854
11.65   11.496
11.248  11.722
11.602  11.888
11.424  11.454
11.312  11.718
10.736  11.68
11.56   11.798
10.028  12.268
9.282   11.976
9.178   11.53
9.954   12.398
9.622   11.558
9.914   11.844
9.07    11.092
10.578  11.354
9.582   12.14
9.622   11.528
9.35    11.71
10.234  11.974
8.986   12.31
9.438   12.11
9.592   12.012
9.666   11.88
9.364   12.012
9.71    11.772
9.992   11.836
9.916   12.028
9.382   12.226
9.808   12.23
9.272   12.152
9.392   11.18
9.28    11.976
9.848   11.632
9.322   11.514
9.718   11.95
9.12    11.76
8.978   12.37
10.072  12.202
9.966   11.822
9.506   11.648
9.702   11.536
9.45    11.96
9.916   11.962
9.96    11.538
9.014   11.744
9.024   11.846
10.296  11.61
7.87    10.838
8.164   10.534
8.214   10.62
8.166   10.698
8.05    10.746
7.978   11.13
8.08    10.992
8.472   11.082
8.494   10.584
8.354   10.38
8.096   10.714
7.882   10.832
7.908   11.346
7.814   10.872
8.28    10.104
8.082   10.676
8.068   10.118
8.116   10.698
8.042   10.79
8.096   10.878
8.124   10.932
8.632   11.124
8.27    10.716
7.622   10.148
8.198   11.398
8.582   11.064
7.942   11.076
8.004   10.574
8.504   11.378
8.118   11.012
7.874   11.296
7.668   10.924
7.966   10.72
7.94    10.996
7.988   11.228
8.164   11.112
8.386   10.772
8.248   10.994
8.286   10.734
8.224   10.316
7.976   9.578
7.876   8.796
8.172   9.01
8.068   9.202
8.416   8.654
8.71    8.458
8.056   8.434
7.304   9.266
8.118   8.608
7.616   9.446
8.092   8.956
8.368   8.968
8.022   9.334
8.32    9.062
7.832   8.952
7.704   8.672
8.236   9.108
8.37    8.904
8.352   8.896
8.046   9.228
7.71    9.538
8.534   8.55
7.996   9.172
8.046   9.204
8.622   9.174
7.776   8.898
8.226   9.038
7.904   9.194
7.874   8.856
7.992   8.952
8.262   9.468
8.088   9.294
8.034   9.792
8.352   9.016
7.85    9.334
8.404   9.366
7.892   8.808
8.202   9.232
7.668   9.026
8.242   9.308
9.432   8.61
10.066  8.19
9.146   8.044
9.662   7.866
9.6 7.874
8.618   8.552
9.334   7.658
9.424   7.83
8.892   8.166
9.386   7.746
9.878   8.054
9.558   7.948
9.222   8.002
9.52    8.282
9.76    7.932
9.568   8.052
9.736   7.552
9.584   8.478
9.358   8.242
9.404   7.79
9.458   8.54
9.482   7.766
8.844   8.024
9.29    8.472
9.274   7.566
9.11    8.014
9.542   7.688
9.432   8.122
9.786   8.066
9.382   7.664
9.404   8.228
9.146   8.158
9.622   8.004
10.286  7.892
9.43    7.676
9.44    8.058
9.788   7.684
9.586   7.91
9.694   7.448
9.576   7.866
11.442  8.688
11.466  8.558
10.674  8.936
11.23   8.126
11.614  8.588
11.59   8.496
11.536  7.586
11.638  8.266
11.16   8.43
10.904  8.532
11.284  8.742
11.25   8.192
10.84   8.218
11.798  8.836
11.51   8.094
10.932  7.796
11.404  8.206
11.088  8.326
11.334  8.17
11.272  8.394
11.59   8.408
11.212  8.516
11.566  8.024
11.246  8.584
11.252  8.566
10.78   8.294
11.04   8.322
11.198  7.886
11.168  8.262
11.88   8.08
11.356  8.586
11.182  8.342
10.836  8.664
11.696  8.906
11.282  8.28
10.718  8.534
10.444  8.684
11.124  8.618
11.392  8.94
11.212  8.308
16.674  9.638
16.162  10.302
16.612  10.218
16.1    9.702
16.404  10.072
15.93   10.106
16.128  9.888
16.41   10.188
15.982  9.92
16.224  10.02
16.296  9.458
16.586  10.174
16.314  10.716
16.278  9.452
16.622  9.652
16.22   9.494
16.626  10.162
16.982  10.596
16.27   10.128
16.202  9.7
16.532  9.776
17.124  9.726
16.47   9.698
16.004  10.28
16.366  9.796
16.268  9.522
16.13   9.748
16.67   10.498
16.488  10.542
16.57   10.21
16.456  10.112
16.482  9.986
16.584  9.754
16.1    9.93
16.226  9.67
16.448  9.566
16.572  9.624
16.436  9.41
16.502  9.98
16.418  9.966
14.362  14.644
14.138  14.63
14.064  15.072
13.692  14.958
14.238  15.296
13.73   15.128
13.952  14.868
13.986  14.77
13.916  14.996
13.874  14.954
14.168  15.276
14.278  15.152
14.098  14.9
13.764  15.212
13.948  14.218
14.13   14.838
13.362  14.932
13.546  14.844
14.13   15.11
13.816  14.602
14.386  14.686
13.786  14.726
14.204  14.822
13.856  15.206
14.074  14.384
13.68   14.988
14.204  14.976
13.388  15.39
13.708  15.048
14.114  15.366
14.4    15.04
14.194  15.04
13.888  15.436
13.958  15.322
13.922  14.802
13.652  14.602
14.294  14.996
13.81   14.526
13.408  15.34
13.834  14.778
8.826   16.474
8.33    16.488
8.468   16.378
8.904   15.846
8.662   16.354
8.684   16.776
8.33    16.066
8.904   16.402
8.778   16.486
8.81    16.458
8.398   16.576
8.542   15.918
9.064   16.456
9.152   16.094
8.614   15.908
8.566   17.012
8.12    16.11
8.844   16.026
8.398   16.282
8.808   15.59
8.502   16.166
8.942   16.19
8.376   16.112
8.518   15.84
8.878   16.004
8.582   16.774
8.248   16.154
8.588   16.24
8.706   16.374
8.524   16.392
8.458   16.452
8.83    16.36
8.616   16.112
8.844   16.362
8.468   15.928
8.62    16.674
8.974   16.53
8.826   16.084
8.104   15.962
8.386   16.24
4.576   12.878
4.46    13.16
3.632   12.862
4.238   12.506
4.348   13.268
3.788   12.372
4.19    12.772
3.86    12.706
3.978   13.308
4.336   12.854
4.218   13.03
4.25    13.002
4.334   13.06
4.654   12.566
4.38    12.792
3.968   13.016
4.614   12.526
3.95    12.67
4.038   12.67
4.426   12.238
4.066   12.514
4.248   12.392
4.61    12.95
4.328   12.99
4.5 12.522
4.176   12.71
4.492   12.464
4.134   12.834
4.316   12.764
4.454   12.084
4.052   12.934
4.26    13.118
4.058   13.718
4.24    12.626
3.838   12.232
4.128   13.4
3.764   12.38
4.424   13.186
4.234   12.994
5.13    13.296
3.9 6.742
3.994   7.206
4.278   7.222
4.172   6.848
3.882   6.894
3.936   6.994
4.162   6.87
3.762   7.1
4.256   7.612
4.55    6.822
4.062   6.984
4.026   7.23
4.364   7.184
4.292   7.208
4.288   6.91
4.018   7.062
4.07    7.104
4.548   7.654
4.402   7.082
3.692   7.49
4.888   7.194
4.456   7.146
4.732   7.154
4.088   7.212
4.502   6.928
3.402   7.434
4.246   6.692
4.166   7.256
4.852   6.83
4.398   7.428
5.016   7.054
4.25    6.76
3.738   7.082
4.254   7.264
4.122   7.238
3.878   7.232
4.55    7.29
4.03    7.126
4.412   7.022
4.276   7.244
8.376   3.788
8.81    3.864
8.218   3.548
8.374   3.748
8.102   4.3
8.386   3.952
8.858   3.274
8.884   3.504
8.294   3.38
8.38    3.178
8.738   4.294
9.1 3.84
9.086   3.6
8.616   3.45
8.624   3.698
8.632   3.82
8.286   3.704
8.816   3.58
8.722   3.854
8.298   3.378
9.014   4.034
8.87    3.554
8.562   3.662
8.6 3.828
8.94    3.836
8.768   4.32
8.838   3.926
8.288   3.466
8.652   3.782
8.376   3.956
7.724   3.414
8.374   4.136
8.6 3.712
9.026   3.788
8.534   3.252
8.874   3.602
8.796   3.888
8.592   3.988
8.98    4.014
8.562   3.856
13.894  4.16
14.278  5.26
14.364  4.748
14.108  4.918
13.998  5.498
14.4    5.296
14.3    5.368
13.958  5.35
13.842  4.984
13.85   4.246
13.978  5.356
14.366  5.104
14.272  4.94
14.336  5.176
14.744  5.248
14.306  5.06
13.986  5.05
14.44   5.33
14.004  4.92
13.332  4.592
14.218  5.544
14.154  4.768
13.468  4.92
13.67   5.406
13.664  5.016
14.12   4.87
13.836  4.51
14.204  5.064
14.004  5.228
13.266  4.858
13.668  5.34
14.528  4.812
14.318  4.592
14.018  5.182
14.37   4.884
14.198  4.804
14.32   4.59
13.636  5.218
14.41   4.656
14.02   5.614

K-means python代码实现：

# coding=utf-8
from numpy import *


def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float, curLine)       #transfer to float
        dataMat.append(fltLine)
    return dataMat


# 计算两个向量的距离，用的是欧几里得距离
def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2)))

'''
    n = shape(dataSet)[1]    #return column
    centroids = mat(zeros((k, n)))
    for j in range(n):
        minJ = min(dataSet[:, j])
        rangeJ = float(max(array(dataSet)[:, j]) - minJ)
        centroids[:, j] = minJ + rangeJ * random.rand(k, 1)
    return centroids
'''

# 随机生成初始的质心（ng的课说的初始方式是随机选K个点）
def randCent(dataSet, k):
    import random
    n = shape(dataSet)[1]  # return column
    cent_return = mat(zeros((k, n)))
    size = len(dataSet)
    centroids = random.sample([i for i in range(size)], k)
    j=0
    for i in centroids:
        cent_return[j] = (dataSet[i])
        j+=1
    return cent_return


def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0]       #return row
    clusterAssment = mat(zeros((m, 2)))  # create mat to assign data points
    # to a centroid, also holds SE of each point
    centroids = createCent(dataSet, k)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):  # for each data point assign it to the closest centroid
            minDist = inf
            minIndex = -1
            for j in range(k):      #cluster
                distJI = distMeas(centroids[j, :], dataSet[i, :])
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i, 0] != minIndex:
                clusterChanged = True
            clusterAssment[i, :] = minIndex, minDist ** 2
        print centroids
        for cent in range(k):  # recalculate centroids
            ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A == (cent))[0]]  # get all the point in this cluster
            if len(ptsInClust):
                centroids[(cent), :] = mean(ptsInClust, axis=0)  # assign centroid to mean
    return centroids, clusterAssment


def show(dataSet, k, centroids, clusterAssment):
    from matplotlib import pyplot as plt
    numSamples, dim = dataSet.shape
    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr', 'xr', 'sb', 'sg', 'sk', '2r', ', ', '+b', '+g', 'pb']
    for i in xrange(numSamples):
        markIndex = int(clusterAssment[i, 0])
        plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])
    #mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '
    #for i in range(k):
        #plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=12)
    plt.show()


def getDataset(filename, k_sample):
    import linecache
    import random
    dataMat = []
    myfile = open(filename)
    lines = len(myfile.readlines())
    SampleLine = random.sample([i for i in range(lines)], k_sample)
    for i in SampleLine:
        theline = linecache.getline(filename, i)
        curLine = theline.strip().split()
        fltLine = map(float, curLine)  # transfer to float
        dataMat.append(fltLine)
    return dataMat


def main():
    dataMat = mat(loadDataSet('R15.txt'))
    myCentroids, clustAssing = kMeans(dataMat, 15)
    print myCentroids
    show(dataMat, 15, myCentroids, clustAssing)


if __name__ == '__main__':
    main()

其中K-means对数据聚类的效果如下图所示：


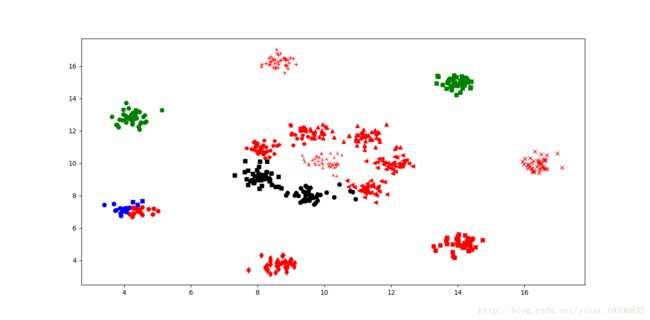
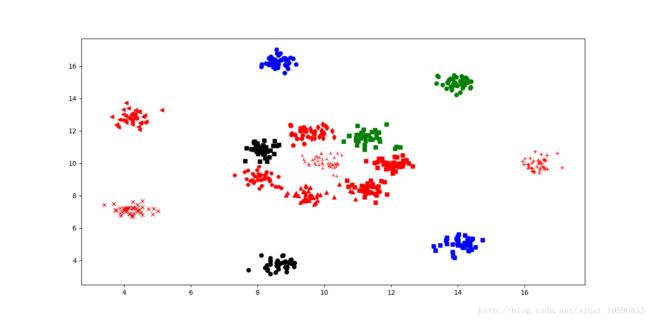
分析上述两幅图可以看到，同样的代码产生的效果却有好有坏，第一幅图效果不是很理想，第二幅图的分类完全正确。根据调试窗口分析原因：由于第一次的数据点都是随机生成，如果K个点里面有两个点很相近，则会出现分类不清的问题。

PAM python代码实现：

# coding=utf-8
import random
from numpy import *


def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split()
        fltLine = map(float, curLine)  # transfer to float
        dataMat.append(fltLine)
    return dataMat


def pearson_distance(vector1, vector2):
    from scipy.spatial.distance import pdist
    X = vstack([vector1, vector2])
    d2 = pdist(X)
    return d2


distances_cache = {}


def totalcost(blogwords, costf, medoids_idx):
    size = len(blogwords)
    total_cost = 0.0
    medoids = {}
    for idx in medoids_idx:
        medoids[idx] = []
    for i in range(size):
        choice = None
        min_cost = inf
        for m in medoids:
            tmp = distances_cache.get((m, i), None)
            if tmp == None:
                tmp = pearson_distance(blogwords[m], blogwords[i])
                distances_cache[(m, i)] = tmp
            if tmp < min_cost:
                choice = m
                min_cost = tmp
        medoids[choice].append(i)
        total_cost += min_cost
    return total_cost, medoids


def kmedoids(blogwords, k):
    import random
    size = len(blogwords)
    medoids_idx = random.sample([i for i in range(size)], k)
    pre_cost, medoids = totalcost(blogwords, pearson_distance, medoids_idx)
    print pre_cost
    current_cost = inf  # maxmum of pearson_distances is 2.
    best_choice = []
    best_res = {}
    iter_count = 0
    while 1:
        for m in medoids:
            for item in medoids[m]:
                if item != m:
                    idx = medoids_idx.index(m)
                    swap_temp = medoids_idx[idx]
                    medoids_idx[idx] = item
                    tmp, medoids_ = totalcost(blogwords, pearson_distance, medoids_idx)
                    # print tmp,'-------->',medoids_.keys()
                    if tmp < current_cost:
                        best_choice = list(medoids_idx)
                        best_res = dict(medoids_)
                        current_cost = tmp
                    medoids_idx[idx] = swap_temp
        iter_count += 1
        print current_cost, iter_count
        if best_choice == medoids_idx: break
        if current_cost <= pre_cost:
            pre_cost = current_cost
            medoids = best_res
            medoids_idx = best_choice

    return current_cost, best_choice, best_res


def show(dataSet, k, centroids, clusterAssment):
    from matplotlib import pyplot as plt
    numSamples, dim = dataSet.shape
    mark =  ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr', 'xr', 'sb', 'sg', 'sk', '2r', ', ', '+b', '+g', 'pb']
    for i in xrange(numSamples):
        # markIndex = int(clusterAssment[i, 0])
        for j in range(len(clusterAssment)):
            if i in clusterAssment[clusterAssment.keys()[j]]:
                plt.plot(dataSet[i, 0], dataSet[i, 1], mark[j])
    #mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '
    #for i in range(k):
        #plt.plot(centroids[i][0, 0], centroids[i][0, 1], mark[i], markersize=12)
    plt.show()


def getDataset(filename, k_sample):
    import linecache
    import random
    dataMat = []
    myfile = open(filename)
    lines = len(myfile.readlines())
    SampleLine = random.sample([i for i in range(lines)], k_sample)
    for i in SampleLine:
        theline = linecache.getline(filename, i)
        curLine = theline.strip().split()
        fltLine = map(float, curLine)  # transfer to float
        dataMat.append(fltLine)
    return dataMat

if __name__ == '__main__':
    dataMat = getDataset('R15.txt',150)
    best_cost, best_choice, best_medoids = kmedoids(dataMat, 15)
    dataMat = mat(dataMat)
    listone = []
    for i in range(len(best_choice)):
        listone.append(dataMat[best_choice[i]])
    show(dataMat, 15, listone, best_medoids)

这里由于运行时间的限制，PAM算法对数据只进行了部分采样处理，可以看到数据点较少。分类效果稳定，但不是最佳。