深度学习(一)autoencoder的Python实现（2）

这一篇章，我将对autoencoder的主要功能进行Python的实现，并通过一个小例子进行验证，其中深度学习和autoencoder的基本原理，在上一篇章深度学习(一)autoencoder的Python实现（1）中解释了，

1类的定义

首先我们建立bean.py文件，在里面定义两个类，一个是神经网络类nn和训练时autoencoder类

import numpy as np
#创建神经网络类
# nodes为1*n矩阵，表示每一层有多少个节点，例如[3,4,5]
# 表示三层，第一层有3个节点，第二层4个，第三层5个
class nn():
    def __init__(self,nodes):#输入为神经网络结构
        self.layers = len(nodes)
        self.nodes = nodes
        self.u = 1.0 # 学习率
        self.W = list() # 权值
        self.B = list() # 偏差值
        self.values = list() # 层值
        self.error = 0 # 误差
        self.loss = 0 # 损失
        for i in range(self.layers-1):
            # 权值初始化，权重范围-0.5~0.5
            self.W.append(np.random.random((self.nodes[i],
            self.nodes[i+1])) - 0.5)   
            # 偏差B值初始化
            self.B.append(0)
        for j in range(self.layers):
            # 节点values值初始化
            self.values.append(0)
#创建autoencoder类，可以看成是多个神经网络简单的堆叠而来
class autoencoder():
    def __init__(self):
        self.encoders = list()
    def add_one(self,nn):
        self.encoders.append(nn)

2方法

建立工具文件util.py，在里面编写相关的调用方法
首先导入包numpy和上文编写的bean

import numpy as np
from bean import nn,autoencoder

建立autoencoder结构方法

#建立autoencoder框架
def aebuilder(nodes):
    layers = len(nodes)
    ae = autoencoder() #获取autoencoder类
    for i in range(layers-1):
        #训练时，我们令输入等于输出，所以每一个训练时的autoencoder层为[n1,n2,n1]形式的结构
        ae.add_one(nn([nodes[i],nodes[i+1],nodes[i]]))   
    return ae

开始进行训练

#训练autoencoder，ae为Autoencoder的训练模型，x为输入，interactions为训练迭代次数
def aetrain(ae,x,interations):
    elayers = len(ae.encoders)
    for i in range(elayers):
        #单层Autoencoder训练
        ae.encoders[i] = nntrain(ae.encoders[i],x,x,interations)
        #单层训练后，获取该Autoencoder层中间层的值，作为下一层的训练输入
        nntemp = nnff(ae.encoders[i],x,x)
        #feed forward
        x = nntemp.values[1]   
    return ae 

其中nntrain即普通的神经网络训练，nnff为feed forward，获取当前前向计算值，下面将代码具体展现

#对神经网络进行训练
def nntrain(nn,x,y,iterations):
    for i in range(iterations):
        nnff(nn,x,y)
        nnbp(nn)
    return nn

前向输出函数，nnff

#前馈函数
def nnff(nn,x,y):
    layers = nn.layers
    # 获取训练样本数量
    numbers = x.shape[0]
    # 赋予初值
    nn.values[0] = x
    for i in range(1,layers):
        nn.values[i] = sigmod(np.dot(nn.values[i-1],nn.W[i-1])+nn.B[i-1])
    # 最后一层与实际的误差
    nn.error = y - nn.values[layers-1]
    # 代价损失
    nn.loss = 1.0/2.0*(nn.error**2).sum()/numbers
    return nn   

其中单层输出y=sigmod(wx+b)，sigmod函数如下

# 激活函数
def sigmod(x):
    return 1.0 / (1.0 + np.exp(-x))

完成nnff后，接下来是最重要的back propagation，nnbp。
本文的损失函数不考虑任何正则项和约束项，为最简单的autoencoder，函数如下


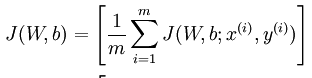
需要涉及到权值更新公式，

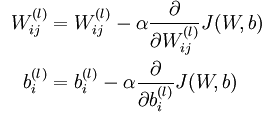
其中 l 为神经网络当前层数， α 为学习速率，我们需要求 α 后的导数项

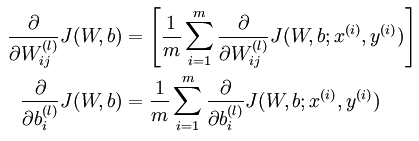
进一步获得

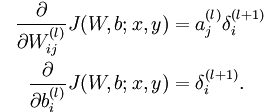
需要求得 δl+1i
当计算最后一层时，

其中f(z)即sigmod函数，f’(z)=f(z)(1-f(z))
当不是最后一层时

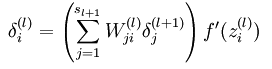
如果对公式有所疑问，可以参考文献Stanford，里面给出了具体说明。
接下来就要展示nnbp代码

#BP函数
def nnbp(nn):
    layers = nn.layers;
    #初始化delta
    deltas = list();
    for i in range(layers):
        deltas.append(0)
    #最后一层的delta为
    deltas[layers-1] = -nn.error*nn.values[layers-1]*(1-nn.values[layers-1])
    #其他层的delta为
    for j in range(1,layers-1)[::-1]:#倒过来
        deltas[j] = np.dot(deltas[j+1],nn.W[j].T)*nn.values[j]*(1-nn.values[j])
    #更新W值和B值
    for k in range(layers-1):
        nn.W[k] -= nn.u*np.dot(nn.values[k].T,deltas[k+1])/(deltas[k+1].shape[0])
        nn.B[k] -= nn.u*deltas[k+1]/(deltas[k+1].shape[0])
    return nn

到这里，完成了工具文件中的代码

3测试

建立test.py，开始我们的小测试

import util
from bean import autoencoder,nn
import numpy as np
# 测试数据，x为输入，y为输出
x = np.array([[0,0,1,0,0],
            [0,1,1,0,1],
            [1,0,0,0,1],
            [1,1,1,0,0],
            [0,1,0,1,0],
            [0,1,1,1,1],
            [0,1,0,0,1],
            [0,1,1,0,1],
            [1,1,1,1,0],
            [0,0,0,1,0]])
y = np.array([[0],
            [1],
            [0],
            [1],
            [0],
            [1],
            [0],
            [1],
            [1],
            [0]])
#################################
# step1 建立autoencoder
#弄两层autoencoder，其中5为输入的维度
nodes=[5,3,2]
#建立auto框架
ae = util.aebuilder(nodes)
#设置部分参数
#训练，迭代次数为6000
ae = util.aetrain(ae, x, 6000)
##############################
# step2 微调
#建立完全体的autoencoder，最后层数1为输出的特征数
nodescomplete = np.array([5,3,2,1])
aecomplete = nn(nodescomplete)
# 将之前训练得到的权值赋值给完全体的autoencoder
# 训练得到的权值，即原来的autoencoder网络中每一个autoencoder中的第一层到中间层的权值
for i in range(len(nodescomplete)-2):
    aecomplete.W[i] = ae.encoders[i].W[0]
# 开始进行神经网络训练，主要就是进行微调   
aecomplete = util.nntrain(aecomplete, x, y, 3000)
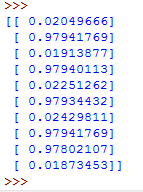
# 打印出最后一层的输出
print aecomplete.values[3]

运行的结果为

还是大致满足要求的。

本章节代码已经上传到github，可以点击链接获得，不过后期会有一定的改进

其中autoencoder 还有很多的改进，比如 sparse autoencoder，denosing autoencoder等，在接下来的章节将会继续用Python实现，还有具体的代码，也会上传。