给信号叠加相位噪声
本Python版本由Alex Bur-Guy(October 2005)发布的Matlab版本翻译而来。
代码如下:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
from scipy import fftpack
import matplotlib.pyplot as plt
def add_phase_noise(Sin, Fs, phase_noise_freq, phase_noise_power, VALIDATION_ON=False):
"""
Oscillator Phase Noise Model
INPUT:
:param Sin: input COMPLEX signal
:param Fs: sampling frequency (in Hz) of Sin
:param phase_noise_freq: frequencies at which SSB Phase Noise is defined (offset from carrier in Hz)
:param phase_noise_power: SSB Phase Noise power (in dBc/Hz)
:param VALIDATION_ON: True - perform validation, False - don't perfrom validation
OUTPUT:
:return Sout: output COMPLEX phase noised signal
NOTE:
Input signal should be complex
EXAMPLE:
Assume SSB Phase Noise is specified as follows:
-------------------------------------------------------
| Offset From Carrier | Phase Noise |
-------------------------------------------------------
| 1 kHz | -84 dBc/Hz |
| 10 kHz | -100 dBc/Hz |
| 100 kHz | -96 dBc/Hz |
| 1 MHz | -109 dBc/Hz |
| 10 MHz | -122 dBc/Hz |
-------------------------------------------------------
Assume that we have 10000 samples of complex sinusoid of frequency 3 KHz
sampled at frequency 40MHz:
Fc = 3e3 # carrier frequency
Fs = 40e6 # sampling frequency
t = np.arange(0, 10000)
S = np.exp(1j * 2 * np.pi * Fc/Fs * t) # complex sinusoid
Then, to produce phase noised signal S1 from the original signal S run follows:
phase_noise_freq = np.array([1e3, 10e3, 100e3, 1e6, 10e6]) # Offset From Carrier
phase_noise_power = np.array([-84, -100, -96, -109, -122]) # Phase Noise power
S1 = add_phase_noise(S, Fs, phase_noise_freq, phase_noise_power)
----------
Original Matlab Version 1.0
Alex Bur-Guy, October 2005
[email protected]
Revisions:
Version 1.5 - Comments. Validation.
Version 1.0 - initial version
NOTES:
1) The presented model is a simple VCO phase noise model based on the following consideration:
If the output of an oscillator is given as V(t) = V0 * cos(w0 * t + phi(t)),
then phi(t) is defined as the phase noise. In cases of small noise
sources (a valid assumption in any usable system), a narrowband modulation approximation can
be used to express the oscillator output as:
V(t) = V0 * cos(w0 * t + phi(t))
= V0 * [cos(w0 * t) * cos(phi(t)) - sin(w0 * t) * sin(phi(t))]
~ V0 * [cos(w0 * t) - sin(w0 * t) * phi(t)]
This shows that phase noise will be mixed with the carrier to produce sidebands around the carrier.
2) In other words, exp(j * x) ~ (1 + j * x) for small x
3) Phase noise = 0 dBc/Hz at freq. offset of 0 Hz
4) The lowest phase noise level is defined by the input SSB phase noise power at the maximal
freq. offset from DC. (IT DOES NOT BECOME EQUAL TO ZERO)
The generation process is as follows:
First of all we interpolate (in log-scale) SSB phase noise power spectrum in M
equally spaced points (on the interval [0, Fs/2] including bounds).
After that we calculate required frequency shape of the phase noise by X(m) = sqrt(P(m) * dF(m))
and after that complement it by the symmetrical negative part of the spectrum.
After that we generate AWGN of power 1 in the freq domain and multiply it sample-by-sample to
the calculated shape
Finally we perform 2 * M - 2 points IFFT to such generated noise
( See comments inside the code)
0 dBc/Hz
\ /
\ /
\ /
\P dBc/Hz /
.\ /
. \ /
. \ /
. \____________________________________________/ /_ This level is defined by the phase_noise_power at the
. \ maximal freq. offset from DC defined in phase_noise_freq
|__| _|__|__|__|__|__|__|__|__|__|__|__|__|__|__|__|__|__|__|__ (N points)
0 dF Fs/2 Fs
DC
"""
if not np.any(np.imag(Sin)):
print("Input signal should be complex signal")
return None
if np.max(phase_noise_freq) >= Fs/2:
print("Maximal frequency offset should be less than Fs/2")
return None
if phase_noise_freq.shape[0] != phase_noise_power.shape[0]:
print("phase_noise_freq and phase_noise_power should be of the same length")
return None
realmin = 2.225073858507201e-308
# Sort phase_noise_freq and phase_noise_power
phase_noise_freq_sorted = np.array([phase_noise_freq[0]])
phase_noise_power_sorted = np.array([phase_noise_power[0]])
for i, phase_noise_freq_i in enumerate(phase_noise_freq):
for j, phase_noise_freq_sorted_j in enumerate(phase_noise_freq_sorted):
if j == 0 and phase_noise_freq_i < phase_noise_freq_sorted_j:
phase_noise_freq_sorted = \
np.insert(phase_noise_freq_sorted, 0, phase_noise_freq_i)
phase_noise_power_sorted = \
np.insert(phase_noise_power_sorted, 0, phase_noise_power[i])
break
elif i != 0 and \
j == phase_noise_freq_sorted.shape[0] - 1 and \
phase_noise_freq_i >= phase_noise_freq_sorted_j:
phase_noise_freq_sorted = \
np.append(phase_noise_freq_sorted, phase_noise_freq_i)
phase_noise_power_sorted = \
np.append(phase_noise_power_sorted, phase_noise_power[i])
break
else:
if i != 0 and \
j != phase_noise_freq_sorted.shape[0] - 1 and \
phase_noise_freq_i >= phase_noise_freq_sorted_j and \
phase_noise_freq_i < phase_noise_freq_sorted[j + 1]:
phase_noise_freq_sorted = \
np.insert(phase_noise_freq_sorted, j + 1, phase_noise_freq_i)
phase_noise_power_sorted = \
np.insert(phase_noise_power_sorted, j + 1, phase_noise_power[i])
break
phase_noise_freq = phase_noise_freq_sorted
phase_noise_power = phase_noise_power_sorted
# Add 0 dBc/Hz @ DC
if phase_noise_freq[0] != 0:
phase_noise_freq = np.insert(phase_noise_freq, 0, 0)
phase_noise_power = np.insert(phase_noise_power, 0, 0)
# Calculate input length
N = Sin.shape[0]
# Define M number of points (frequency resolution) in the positive spectrum
# (M equally spaced points on the interval [0, Fs/2] including bounds),
# then the number of points in the negative spectrum will be M - 2
# (interval (Fs/2, Fs) not including bounds)
#
# The total number of points in the frequency domain will be 2 * M - 2, and if we want
# to get the same length as the input signal, then
# 2 * M - 2 = N
# M - 1 = N/2
# M = N/2 + 1
#
# So, if N is even then M = N/2 + 1, and if N is odd we will take M = (N + 1)/2 + 1
if N % 2 == 1:
M = (N + 1)/2 + 1
else:
M = N/2 + 1
M = int(M)
# Equally spaced partitioning of the half spectrum
F = np.linspace(0, Fs/2, M) # % Freq. Grid
dF = np.append(np.diff(F), F[-1] - F[-2]) # Delta F
# Perform interpolation of phase_noise_power in log-scale
intrvlNum = phase_noise_freq.shape[0]
logP = np.zeros(M)
for intrvlIndex in range(intrvlNum):
leftBound = phase_noise_freq[intrvlIndex]
t1 = phase_noise_power[intrvlIndex]
if intrvlIndex == intrvlNum - 1:
rightBound = Fs/2
t2 = phase_noise_power[-1]
inside = []
for i in range(F.shape[0]):
if F[i] >= leftBound and F[i] <= rightBound:
inside.append(i)
else:
rightBound = phase_noise_freq[intrvlIndex + 1]
t2 = phase_noise_power[intrvlIndex + 1]
inside = []
for i in range(F.shape[0]):
if F[i] >= leftBound and F[i] < rightBound:
inside.append(i)
logP[inside] = t1 + \
(np.log10(F[inside] + realmin) - np.log10(leftBound + realmin)) / \
(np.log10(rightBound + realmin) - np.log10(leftBound + realmin)) * \
(t2 - t1)
P = 10**(logP.real/10)
# Now we will generate AWGN of power 1 in frequency domain and shape it by the desired shape
# as follows:
#
# At the frequency offset F(m) from DC we want to get power Ptag(m) such that P(m) = Ptag/dF(m),
# that is we have to choose X(m) = sqrt(P(m) * dF(m));
#
# Due to the normalization factors of FFT and IFFT defined as follows:
# For length K input vector x, the DFT is a length K vector X,
# with elements
# K
# X(k) = sum x(n)*exp(-j*2*pi*(k-1)*(n-1)/K), 1 <= k <= K.
# n=1
# The inverse DFT (computed by IFFT) is given by
# K
# x(n) = (1/K) sum X(k)*exp(j*2*pi*(k-1)*(n-1)/K), 1 <= n <= K.
# k=1
#
# we have to compensate normalization factor (1/K) multiplying X(k) by K.
# In our case K = 2 * M - 2.
# Generate AWGN of power 1
if not VALIDATION_ON:
awgn_P1 = np.sqrt(0.5) * (np.random.randn(M) + 1j * np.random.randn(M))
else:
awgn_P1 = np.sqrt(0.5) * (np.ones(M) + 1j * np.ones(M))
# Shape the noise on the positive spectrum [0, Fs/2] including bounds (M points)
X = (2 * M - 2) * np.sqrt(dF * P) * awgn_P1
# Complete symmetrical negative spectrum (Fs/2, Fs) not including bounds (M - 2 points)
X = np.append(X, np.fliplr(np.conj(X[1: -1]).reshape(1, -1)).reshape(-1))
# Remove DC
X[0] = 0
# Perform IFFT
x = fftpack.ifft(X)
# Calculate phase noise
phase_noise = np.exp(1j * np.real(x[: N]))
# Add phase noise
if not VALIDATION_ON:
Sout = Sin * phase_noise[: Sin.shape[0]]
else:
Sout = "VALIDATION IS ON"
if VALIDATION_ON:
plt.figure()
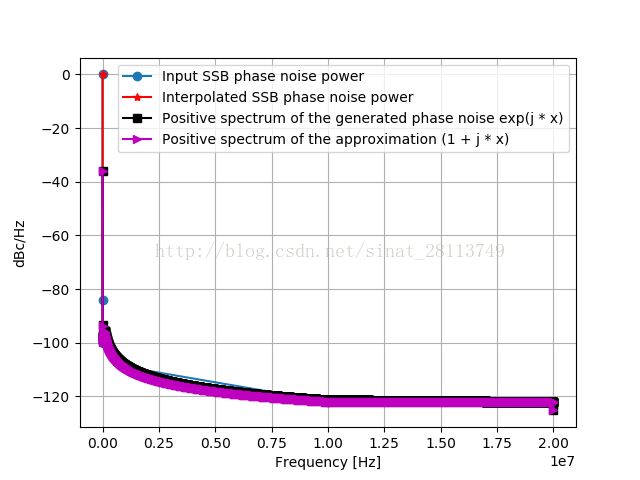
plt.plot(phase_noise_freq, phase_noise_power, 'o-', \
label='Input SSB phase noise power')
plt.grid()
plt.plot(F, 10 * np.log10(P), 'r*-', \
label='Interpolated SSB phase noise power')
X1 = fftpack.fft(phase_noise)
plt.plot(F, 10 * np.log10(((np.abs(X1[: M])/np.max(np.abs(X1[: M])))**2)/dF[0]), 'ks-', \
label='Positive spectrum of the generated phase noise exp(j * x)')
X2 = fftpack.fft(1 + 1j * np.real(x[: N]))
plt.plot(F, 10 * np.log10(((np.abs(X2[: M])/np.max(np.abs(X2[: M])))**2)/dF[0]), 'm>-', \
label='Positive spectrum of the approximation (1 + j * x)')
plt.xlabel('Frequency [Hz]')
plt.ylabel('dBc/Hz')
plt.legend()
plt.show()
return Sout
# %%
def test():
Fc = 3e3 # carrier frequency
Fs = 40e6 # sampling frequency
t = np.arange(0, 10000)
S = np.exp(1j * 2 * np.pi * Fc/Fs * t) # complex sinusoid
phase_noise_freq = np.array([1e3, 10e3, 100e3, 1e6, 10e6]) # Offset From Carrier
phase_noise_power = np.array([-84, -100, -96, -109, -122]) # Phase Noise power
S1 = add_phase_noise(S, Fs, phase_noise_freq, phase_noise_power, True)
return None
if __name__ == "__main__":
test()
Python版本运行结果分别如下:
Matlab版本运行结果如下: