《Python数据分析与挖掘实战》第六章学习拓展——偷漏税用户识别

本文是继上一篇文章中上机实验之后的拓展思考部分的练习记录。此拓展思考部分主要目标是依据附件所提供的汽车销售企业的部分经营指标，来评估汽车销售行业纳税人的偷漏税倾向，建立偷漏税行为识别模型。
本次拓展思考练习分以下几个步骤进行：

1. 数据初步探索分析
2. 数据预处理
3. 模型选择与建立
4. 模型比较

接下来将逐一进行记录。

一 数据初步探索分析

在这一部分，将对附件中所提供的数据进行初步研究，查看其可能存在的内部规律。
首先自然是数据的导入，代码如下：

df=pd.read_excel('C:/Python27/Lib/site-packages/xy/chapter6/拓展思考/拓展思考样本.xls'.decode('utf-8'))

需要说明的是，刚开始导入的时候，由于路径中包含中文，因此发生错误，通过百度，在路径后添加.decode(‘utf-8’)进行了编码转换，最后才得以成功导入。
附件中一共包含124个样本，16个变量，其中一个是纳税人编号，一个是是否偷漏税的输出结果，不偷税为正常，存在偷漏税则为异常，其他都为与偷漏税相关的经营指标。接下来将分别从分类变量和数值型变量两个方面入手对数据做一个探索性分析。

1.1 偷漏税情况下的销售类型和销售模式分布

销售的汽车类型和销售模式可能会对偷漏税倾向有一定的表征，因此，画出【输出结果为异常的销售类型和销售模式】的分布图可能可以直观上看出是否有一定影响。
代码如下：

fig=plt.figure()
fig.set(alpha=0.2)
#不同销售类型和销售模式下的偷漏税情况
plt.subplot2grid((1,2),(0,0))
df_type=df[u'销售类型'][df[u'输出']=='异常'].value_counts()
df_type.plot(kind='bar',color='blue')
plt.title(u'不同销售类型下的偷漏税情况',fontproperties='SimHei')
plt.xlabel(u'销售类型',fontproperties='SimHei')
plt.ylabel(u'异常数',fontproperties='SimHei')
plt.subplot2grid((1,2),(0,1))
df_model=df[u'销售模式'][df[u'输出']=='异常'].value_counts()
df_model.plot(kind='bar',color='green')
plt.title(u'不同销售模式下的偷漏税情况',fontproperties='SimHei')
plt.xlabel(u'销售模式',fontproperties='SimHei')
plt.ylabel(u'异常数',fontproperties='SimHei')
plt.subplots_adjust(wspace=0.3)
plt.show()

运行结果如下图：

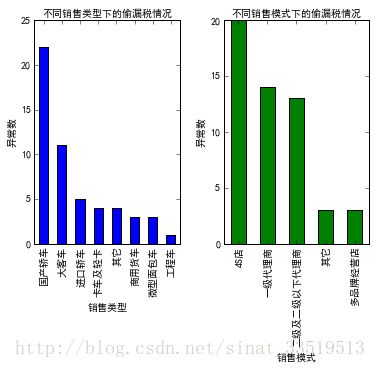
由图可以看出在存在偷漏税情况的纳税人中，销售国产轿车最多，通过4S店进行销售的最多。
这只是一个分布情况，具体是否有关系，在这里并不确定。
问题记录：在画这个柱形图的时候，刚开始，所有的中文都无法显示，在进行资料查找之后，知道是中文字体的问题，需要自己定义中文字体，因此在代码中加入：

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False

按理说，这样就可以显示中文。但是博主在运行的时候，依旧无法显示中文，后来在cmd运行窗口中运行出来的图却能正常显示中文，因此作出判断，应该是所用平台，也就是Python（x,y）的问题。而在第二天重新打开Python(x,y)并运行的时候发现可以正常显示，所以，应该就是环境的问题，而不是代码的问题。

1.2数值型数据分布情况

源数据分布我也看不出什么规律来，因此，这里就简单针对正常和异常这两种输出情况进行了describe，代码如下：

#不同输出情况下的数值型变量总体情况
df_normal=df.iloc[:,3:][df[u'输出']=='正常'].describe().T
df_normal=df_normal[['count','mean','max','min','std']]
df_abnormal=df.iloc[:,3:][df[u'输出']=='异常'].describe().T
df_abnormal=df_abnormal[['count','mean','max','min','std']]

输出的结果如下：
正常情况：

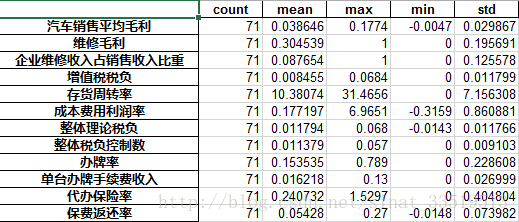
异常情况：

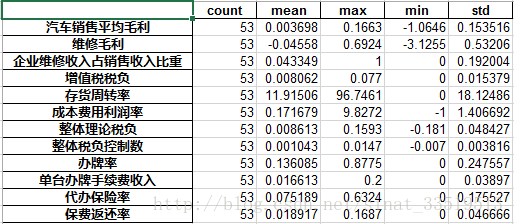
从平均值可以大概看出，当输出结果为正常和异常两种情况时，还是有不一样的，特别是汽车销售平均毛利、维修毛利、代办保险率等还是比较明显的，但这只是初步的一个观察结果，只能作为一个猜想来考虑。

二 数据预处理

数据预处理包括异常值、缺失值的处理，数值的转换等。本文中数据没有缺失值，因此不用对缺失值进行处理，但是博主对汽车销售经营指标实在不了解，所以看不出来哪些值有异常，因此暂且不对数值进行处理，但是涉及到分类变量，在模型建立时，需将分类变量转换成虚拟变量，因此，博主在数据预处理的过程中，主要对销售类型、销售模式以及输出进行虚拟变量的建立。
Pandas中有直接转换的函数，get_dummies。
虚拟变量建立代码如下：

#数据预处理（将销售类型与销售模式以及输出转换成虚拟变量）
type_dummies=pd.get_dummies(df[u'销售类型'],prefix='type')
model_dummies=pd.get_dummies(df[u'销售模式'],prefix='model')
result_dummies=pd.get_dummies(df[u'输出'],prefix='result')
df=pd.concat([df,type_dummies,model_dummies,result_dummies],axis=1)
df.drop([u'销售类型',u'销售模式',u'输出'],axis=1,inplace=True)
#正常列去除，异常列作为结果
df.drop([u'result_正常'],axis=1,inplace=True)
df.rename(columns={u'result_异常':'result'},inplace=True)

三 模型选择与建立

博主在这篇文章中选择的模型为上一篇文章中用的CART决策树模型和逻辑回归模型。
首先不管哪种模型，都需要先进行数据划分，即将数据分成训练数据和测试数据两部分，与上一篇文章一样，这里依旧选取80%作为训练数据，20%作为测试数据。
代码如下：

#数据划分(80%作为训练数据，20%作为测试数据)
data=df.as_matrix()
from random import shuffle
shuffle(data)
data_train=data[:int(len(data)*0.8),:]
data_test=data[int(len(data)*0.8):,:]

接下来将分别训练CART决策树模型和逻辑回归模型。

3.1 CART决策树模型

CART决策树模型在上一篇文章中已经讲过，代码也基本不变，在这里就不再赘述。在模型建立之后，与上一篇文章相同，也进行了混淆矩阵的绘制，这里不仅绘制训练样本的混淆矩阵，也将测试样本的混淆矩阵画出。
代码如下：

#确定y值和特征值
y=data_train[:,-1]
x=data_train[:,1:-1]
from sklearn.tree import DecisionTreeClassifier #导入决策树模型


tree = DecisionTreeClassifier() #建立决策树模型
tree.fit(x, y) #训练

#保存模型
from sklearn.externals import joblib
joblib.dump(tree, 'C:/Python27/Lib/site-packages/xy/chapter6/thoughts_tree.pkl')

from cm_plot import * #导入混淆矩阵可视化函数
cm_plot(y, tree.predict(x)).show() #显示混淆矩阵可视化结果

cm_plot(data_test[:,-1],tree.predict(data_test[:,1:-1])).show()

训练样本和测试样本的混淆矩阵如下所示：
训练样本：

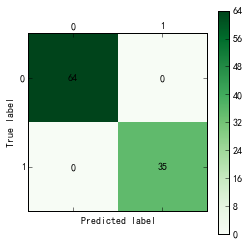
测试样本：

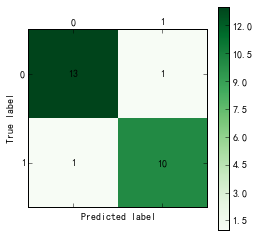
可以看出，对于训练样本来说，决策树模型的正确率为100%，而对于测试样本，其准确率为23/25=92%，其中，正常用户中，被判定为偷漏税用户的比例为1/14=7.1%，偷漏税用户中，被判定为正常用户的比例为1/11=9.1%。

3.2 逻辑回归模型

逻辑回归属于机器学习中较为简单的模型。在Andrew NG的机器学习课中，最开始就讲了逻辑回归模型，是在线性模型上套用一个逻辑函数。具体可以参考下面这篇文章：
逻辑回归模型基础
也可以参考Andrew NG的《Machine Learning》课程讲义。（之前上这门课的时候没有想到可以在博客里做笔记来记录，以后有时间可以考虑补上，或者以后可以另设理论知识版块对数据分析涉及到的理论知识记录，以供日后参考回顾。）
在Python中实现逻辑回归模型的时候，可以直接从sklearn包中导入线性模型linear_model，就可以直接对逻辑回归模型进行调用，模型建立之后同样分别绘制训练样本和测试样本的混淆矩阵，并且输出逻辑回归的系数。
代码如下：

#逻辑回归
from sklearn import linear_model
clf=linear_model.LogisticRegression(C=1.0,penalty='l1',tol=1e-6)
#此处的x,y与上文中决策树所用x,y相同
clf.fit(x,y)
#逻辑回归系数
xishu=pd.DataFrame({"columns":list(df.columns)[1:-1], "coef":list(clf.coef_.T)})
#逻辑回归混淆矩阵
cm_plot(y,clf.predict(x)).show()
#对test数据进行预测
predictions=clf.predict(data_test[:,1:-1])
#test混淆矩阵
cm_plot(data_test[:,-1],predictions).show()

训练样本和测试样本的混淆矩阵如下：
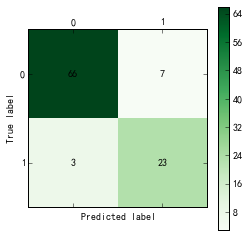
训练样本：

测试样本：

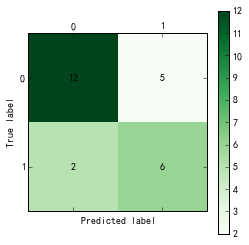
由图可以看出，对于训练样本，逻辑回归模型的准确率为（23+66）/99=89.9%，其中，正常用户中，被判定为偷漏税用户的比例为7/73=9.6%，偷漏税用户中，被判定为正常用户的比例为3/25=12%；测试样本的准确率为18/25=72%，其中，正常用户中，被判定为偷漏税用户的比例为5/17=29.4%，偷漏税用户中，被判定为正常用户的比例为2/8=25%。
得出逻辑回归的系数为：

可以通过系数看出，维修毛利、代办保险率、4S店对偷漏税有明显的负相关，成本费用利润率、办牌率、大客车和一级代理商对偷漏税有明显的正相关。也就是说，纳税人维修毛利越高，代办保险率越高，通过4S店销售，其偷漏税倾向将会越低；而纳税人成本费用利润率、办牌率越高，销售类型为大客车，销售模式为一季代理商，那么该纳税人将更有可能为偷漏税用户。

四 模型比较

通过第三部分中的混淆矩阵和准确率计算，可以发现，不管是针对训练样本还是测试样本，CART决策树模型都比逻辑回归模型效果要更好一些，为了进一步比较两个模型的性能，博主绘制了两个模型的ROC曲线，ROC曲线绘制的代码与上一篇文章差不多。
具体代码如下所示：

#两个分类方法的ROC曲线
from sklearn.metrics import roc_curve #导入ROC曲线函数
import matplotlib.pyplot as plt
fig,ax=plt.subplots()
fpr, tpr, thresholds = roc_curve(data_test[:,-1], tree.predict_proba(data_test[:,1:-1])[:,1], pos_label=1)
fpr2, tpr2, thresholds2 = roc_curve(data_test[:,-1], clf.predict_proba(data_test[:,1:-1])[:,1], pos_label=1)
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of CART', color = 'blue') #作出ROC曲线
plt.plot(fpr2, tpr2, linewidth=2, label = 'ROC of LR', color = 'green') #作出ROC曲线
plt.xlabel('False Positive Rate') #坐标轴标签
plt.ylabel('True Positive Rate') #坐标轴标签
plt.ylim(0,1.05) #边界范围
plt.xlim(0,1.05) #边界范围
plt.legend(loc=4) #图例
plt.show() #显示作图结果

做出的两个模型的ROC曲线如下图所示：

上篇文章中已经提到，ROC曲线越靠近左上角，则模型性能越优，当两个曲线做于同一个坐标时，若一个模型的曲线完全包住另一个模型，则前者优，当两者有交叉时，则看曲线下的面积，上图明显蓝色线下的面积更大，即CART决策树模型性能更优。
由此可见，对于本文中的例子来说，CART决策树模型不管从混淆矩阵来看，还是从ROC曲线来看，其性能都要优于逻辑回归模型。

五 总结

到此，关于拓展思考的部分就练习完毕了。在本次拓展思考中，对于博主来说最主要的“成就”是对于本章节中所涉及到的数据分析基本流程、CART决策树模型的建立、混淆矩阵的绘制以及ROC曲线的绘制都再次进行了复习巩固，对逻辑回归的Python实现进行了尝试，对于画图中涉及到的一些小问题也进行了解决，还是比较满意的。
最后有一点遗留的小问题也做一下记录，在运行文件的时候，发现混淆矩阵图和ROC曲线图几乎每一次运行结果都不一样，除了CART决策树模型的训练样本，也就是准确率为100%的那个图是不变的，其他的图一直都在变化，说明预测结果一直都在变化。不知道哪里有问题，暂且先放着吧–