共识梳理 及 Hashgraph简评
所有今天正好借撸Hashgraph的机会先简单地梳理下共识的知识点。
在一个分布式系统中,为了使得整个系统正常工作,一个久远而又核心的问题就是如何保证集群中所有节点中的数据完全相同并且能够对发起的提案达成一致。共识算法就是用来解决上述问题,从而保证分布式系统一致性的方法。
虽然说到共识算法,如今区块链届的人张口闭口就来POW, POS, DOPS, 但是共识的定义却又是另外一番面目:
共识定义:
终止性(Termination): 所有正常运作的进程(节点)最终会在有限步数中结束并做出决定, 算法不会无尽执行下去。
一致性: 所有进程必须做出相同的决定(意见一致 Agreement);如果所有进程都提议相同的初始决定值,那么所有正确进程都应选择该值(行为统一Integrity)。
有效性(Validity): 最终达成一致的决定必须是其他进程提交值中的某一个。
节点的失效,节点之间网络通信收到干扰甚至阻断,以及分布式系统的运行速度的差异都会使得分布式系统难以达成一致。
著名的拜占庭将军问题专门研究了如何处理分布式系统中的错误节点(所谓容错)。Leslie Lamport(共识届的真大牛)在1982年发布的The Byzantine Generals Problem论文中提出的这个模型,可以算是分布式领域中最复杂、最严格的容错模型:系统不会对集群中的节点做任何的限制,错误节点可以做任何坏事,比如延迟响应、不进行响应,发送错误信息、发送随机消息、对不同节点发送不同决定,不同错误节点私下串通来搞事,大魔王横空出世控制多个节点实施有预谋的攻击等等。总之,现实中应该找不到比这个模型中更坏更恶劣的节点们了,他们的行为带有主观恶意且无法被预测。唯一可以保证的是每条消息的原始内容不会被篡改,消息的来源也都可以被判断出来的。
拜占庭将军问题是对分布式系统容错的最高要求,在这么一个极度悲观的场景下,这篇82年的论文提出的原始拜占庭容错算法(BFT)证明了只要系统中的坏节点占三分之一以下,系统还是能被抢救过来的。论文提出了口头算法和书面算法(书面算法加了数字签名溯源机制做优化),如果你熟悉CS递归算法的话,应该不难看懂。
基本思路是从所有节点中选出一个“将军”,剩下都是“副官”。在将军把决定发给其他副官后,每一个副官(比如副官A)会作为新一轮的将军,再询问其他所有副官收到来自于将军的决定是什么,因为将军有可能是坏人,副官需要采取多方验证。然后由于成为了新一轮将军的副官A也会被怀疑为坏人,所以收到副官A消息的每个其他副官也需要各自作为将军再进行下一轮的问询,来确认各自收到来自于副官A的决定是什么。以此类推,每次递归做的都是最悲观的假设。如若分布式系统中一共有n个节点以及f个坏节点,则每一节点需要发送的信息数是(n-1)(n-2)..(n-f-1),复杂度很高。具体算法如下:
之后学术界提出过各种BFT的算法,其中特别著名的是在1999年由Miguel Castro和Barbara Liskov提出的PBFT,实用拜占庭容错算法。值得一提的是其中叫做Liskov的作者就是提出了LSP (SOLID principles之一)的那个大牛“里氏”。
这个算法将原始BFT的算法复杂度由指数级降低到多项式级,使得拜占庭容错算法在实际系统应用中变得可行。
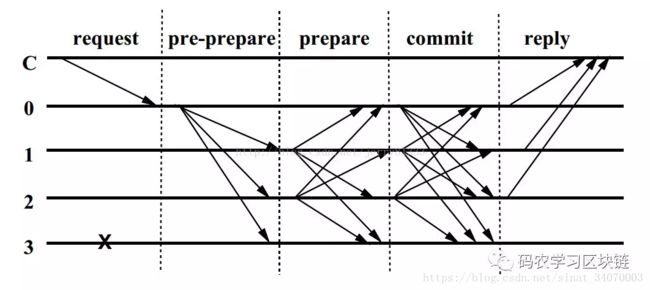
PBFT同样要求坏节点少于三分之一,并且额外要求网络封闭,即节点数目提前确定并且节点互相联通。算法主要依赖预准备(pre-prepare),准备(prepare)和提交(commit)这三个主要阶段。客户端需要等待f+1个从不同副本节点得到的相同响应,响应需要被正确签名,并且具有同样的时间戳和执行结果r。这样客户端才能把r作为正确的执行结果。因为失效的副本节点不超过f个,所以f+1个副本的一致响应必定能够保证结果是正确有效的。消息复杂度最少是O(n^2),确实性能提高了不少。
总的来说,BFT模型非常严苛, 大多数实际的分布式系统并不需要考虑 那么恶劣的环境。大牛Lamport另外提出过的Poxas共识就是一系列非拜占庭的完备容错协议,旨在让不存在恶意节点的分布式网络在出现节点错误时仍然能保持一致(这里假设了当一个节点出现故障时,它只是停止工作而不回复消息而已)。
而且相比公链的,BFT更适合联盟链和私链。一方面虽然PBFT把消息传播的开销改善到了节点数量平方的规模,但是面对节点数量庞大的公链网络,依然会导致低效的共识执行,另一方面公链本身是个动态网络,新节点可以随意加入也增加了执行难度。
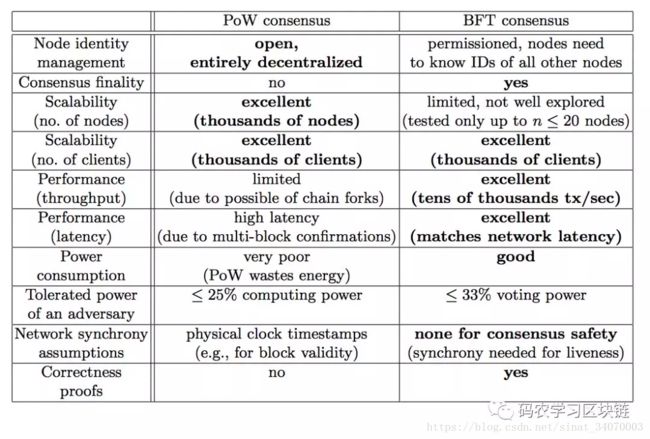
这里顺带提下POW。POW是目前最令人信服的用于公链的共识算法,被人诟病主要在于POW为了使得主链不分叉,强制矿工来解决复杂且无意义的问题(该问题运算复杂但是验证容易),该手段消耗了极大的能源来做无效计算,且共识达成慢,交易吞吐量低下。POW的算法思路是通过增加提案的成本来限制一段时间内整个网络出现提案的个数,并且放宽了对最终一致性的严格确认,只要求沿着最长链进行接续。所以POW下的系统只有概率意义上的最终确认,而无法确定某一时刻全网达到了共识。不过如果能搞出一个只做有效计算的POW,应该是一个有前途的方向。以下是POW和BFT的对比:
再说回BFT,BFT的世界里基本都是默认使用同步通信。这里要引入一个著名的理论,即FLP不可能定理,这是是分布式系统领域最重要的定理之一,它给出了一个非常重要的结论:在网络可靠并且存在节点失效的异步分布式系统中,即使只有一个进程节点失败,则不存在任何一个可以解决一致性问题的确定性共识算法。算是个很惊人的断言了,并且成功阻止了人类在这条路上的无效研究。
除了以上POW和BFT这两大体系外,还有POS,DPOS这些毁誉参半的存在,虽然相比POW,POS展现了很多优势,但是天然也面临着各种分叉的风险,有来自于理性的矿工的故意低成本分叉,也有来自于低权益者单车变摩托驱动下的恶意攻击。
另外一个比较有意思的体系是DAG(有向无环图)上的共识,比如SPECTRE。DAG作为一种数据结构其实就和链(Chain)本身一样,并没有什么神秘的,在大部分情况下,把DAG系的链叫做BlockDAG没什么毛病。DAG和单链比起来就是前者先上车(出块)再买票(共识,获得一致性),后者是先买票再上车。所以DAG系的链都是动辄吹嘘自己百万并发,先疯狂出完块,然后再一起捋出一个最长链来做主链。由于其拓扑结构的复杂性,以及出块和共识的天然顺序,在双花问题上DAG比传统单链要麻烦不少。像SPECTRE这种的共识引入了投票机制,将DAG的拓扑结构翻译成了投票。节点互相不交流,也不参与投票,投票者是区块本身,区块会为自己所置身于的链投出支持票。
有了以上的知识储备,应该可以开始谈及Hashgraph。Hashgraph可谓是博采众长,所运用和借鉴的科技几乎是涵盖以上的每个点。其中值得称道的分别是公链环境下做异步BFT共识,八卦协议用于传播八卦本身的关系和拓扑结构(DAG)以及虚拟投票。
为什么Hashgraph可以异步BFT?
之前已经说过了FLP不可能理论否决了异步BFT共识的可能性,不过Hashgraph对共识定义中的终结性做了些许放宽,即it is possible for a nondeterministic system to achieve consensus with probability one,这里的paobablity one是相对于guaranteed来说的, 指的是有一定概率下共识算法会无限期的被执行下去,但是这种情况发生的概率很小,接近为0。再换句话说,类似于最终终结性(eventually),即“XX虽会迟到,但绝不会缺席”。所以Hashgraph的共识算法可以是完全异步的(信息可以被无限延迟),非确定性的,且“拜”迟但到。 而且共识算法中没有引入任何领导的角色, 从而规避了领导节点被DoS攻击导致系统问题的风险。
为什么Hashgraph中BFT可能可以用到公链?
之前说到BFT的一大问题是消息复杂度太高,大量消耗系统的网络带宽,而且无法很好的应对动态网络。这里Hashgraph很聪明的引入了传统CS里的八卦协议(Gossip protocol),并且加以了独特的创新,另外再加上虚拟投票,于是在需要共识的时候并不是要突发的大规模消息传递。
Gossip算法灵感来自办公室八卦,只要两个人之间八卦一下,在有限的时间内所有的人都会知道该八卦的信息,别名“八卦算法”,“闲话算法”、“病毒感染算法”或“谣言传播算法”。八卦算法在分布式p2p的场景中获得了大成功,可以很好的当作节点状态传播和管理的手段。本质上八卦算法是一个带冗余的容错算法,更进一步,八卦是一个最终一致性算法或提供一致性算法的手段。虽然无法保证在某个时刻所有节点状态一致,但可以保证在最终某个时刻所有节点一致对某个时间点前的所有历史达成一致。
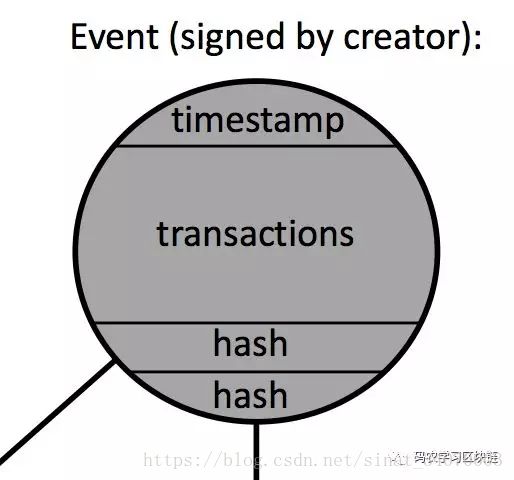
而且Hashgraph让节点之间八卦的内容是节点间互相八卦的历史记录——被称为散列图(hashgraph)的数据结构。每个节点就在不停维护这个数据结构,并在八卦中把自己知道的事件(Event)散播出去。本质上Hashgraph就是个变种DAG(每个点可以有两个父节点),它里面的端点就是事件(Event),里面可以包括任何内容,数据或者交易事务,其实就是个容器,我觉得把事件当成区块可能更加容易被大部分所理解。之所以Hashgraph不直接把事件叫做区块源于Hashgraph的高逼格,人家作为一个创新的共识算法只是顺手实现了分布式账本,解决区块链的问题,而不是把区块当作一个第一大问题来解决的。 下文会统一用区块来代替事件,方便阐述。
上图就是一个区块的模样,其中包含区块创建的时间戳,该区块愿意包括的所有交易事务数据,以及两个指向父节点的hash指针。
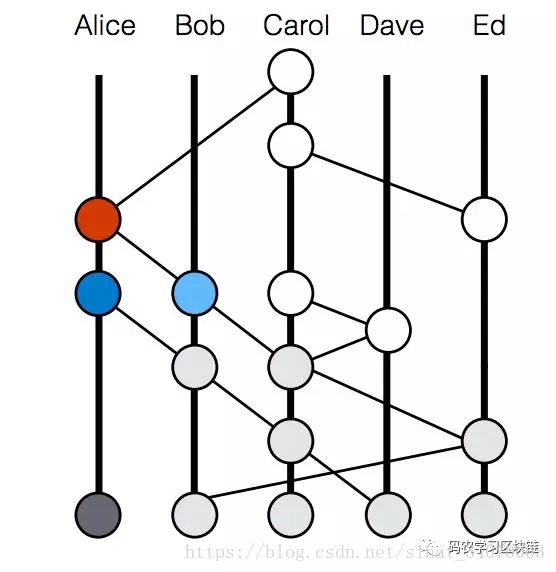
这第二个图中描述了多个区块连成的散列图,其中每个纵轴是每个不同的节点,其中的圆圈就是区块,越靠近下方的越早出的区块,越靠近上方是越新的快。
当Bob这个话痨随机找到了Alice拉家常的时候,就会把自己当前所知道的一切都原原本本的告诉Alice。然后Alice这里会出一个新块(红点),这个新块里除了加入新的交易事务的同时,还会加上两个指向父区块的hash值,一个指向自己的最新区块(深蓝),一个指向Bob和自己聊天时候最新的区块(天蓝)。Git也是使用hash实现链接的,只不过是单父亲模式。这也是散列图得名的原因,本质上就是一个靠hash连接起区块的图谱。只不过这里的重点不是把具体每个区块叫做事件还是其他什么名字,而是连接本身和其拓扑结构。
由于每个节点都会通过八卦维护一个散列图,所以每个节点计算共识投票的时候可以发起虚拟投票,也就是计算其他节点在给定的散列图中会怎么投票,从而不需要在网络上再做大量双向同步通信。
此外,可以通过打包,压缩和各种优化来使得八卦所占用的带宽变少。
在某一时刻,不同节点的散列图中最新的区块可能都各不一样,但是更早些的区块和继承关系都是一致的, 而且随着时间的推逝和八卦的积极进行,他们的散列图会收敛到相同的结果。这里的一致指的是如果两个节点的散列图里都有区块x,那么这两个x都会指向相同的两个父区块。
Hashgraph特别关注公平性,即交易事务的实际顺序。这在有些场景下是必须的,比如交易所,谁先下单买了同一只股票是需要被明确厘清的。所以Hashgraph里每个节点都会试图整理区块的顺序,这时节点就会对自己发起共识提案,例如“区块a是否早于区块b”,然后节点会照着自己保存的散列图有如精分一般遵从写死的代码逻辑和规则的从每个已知节点的角度进行投票计票和共识运算。这里的共识是异步的,意味着每个节点会在不同时间点发起虚拟投票,做出决定,并且自信满满地相信这个提案在全网络下会获得相同的决定(即共识)。还是那句话,共识迟早会进行并达成,只是有早有晚。
话说如果Alice作假,自己产生了两个新区块b和c都指向自己的最后的一块区块a,那么在Alice的纵轴上就会从链状变成树状,等于进行了分叉攻击。如果Alice把b的存在告诉了Bob,而把c的存在告诉了Carol,那么Bob和Carol这两个节点所进行的虚拟投票就会变得不一样。为了防止这个问题的发生,Hasgraph引入了可见(Seeing)和强可见(Strongly seeing)的概念。
区块y“可见”区块x意味这区块x是区块y的祖先,y可以通过某个指针通路找到x。但是如果一个坏节点创建了两个平级(即分叉)的区块a和b,并且都是另外一个区块w的父节点,那么这种情况下定义区块w不可见a,也不可见b,因为每个区块按道理只能有最多一个属于同一个节点创造的同级区块。
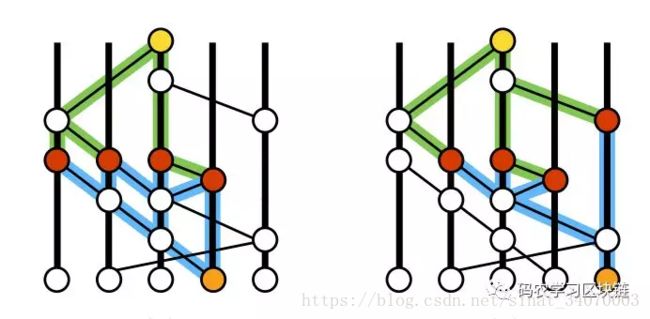
“强可见”是个关键点,它定义了如果区块x“强见”了(errr..就这样吧...)区块y,那么意味着x和y的连线之间的区块能跨越绝对多数的节点(假设n是节点数目,那么绝对多数指的就是大于n的三分之二,并且绝大多数的定义可以被扩展到POS语境下,即大于2/3总权重,从而转为POS共识。比如下图中,黄区块可以强见橙区块,因为他们自己本身以及他们之间的连线路径中经历的中间区块遍及了绝对多数的参与节点。
强可见保证了两个节点在虚拟计票的时候,能够获得一致的结果。从而为作为Hashgraph能够达成最终拜占庭一致的理论基础。
后续论文中有论证,如果w是非法分叉的两个分支上区块的后继区块,难么他要么强见a要么强见b,不会同时强见a和b。
Hashgraph还引入了不少新概念,比如轮次(round),见证人(Witness)知名见证人(Famous witnesses)。
创建轮次(created round): 如果一个父区块的创建轮次是r,那么它的子区块的轮次要么也是r,要么是r+1。很显然,子区块不可能拥有比父区块还早的创建轮次。当且仅当子区块强见了r轮中绝大多数的见证人,那么它的轮次会加一。
见证人:每一节点在每一轮次中创建的第一个区块被称为见证人(也可看作该轮次中相对的先祖区块)。某节点也有可能在某一轮次中没有创建见证人区块。下文中也会在某些上下文中将见证人直接称作第x轮先祖,虽然可能有歧义,但是在特定语境下会更加便于理解。
知名见证人:如果上述见证人区块在被创建出来之后就被很快得传播到了其他节点上,那么这些见证人区块就可以被称作知名见证人。更具体的说,如果第r轮的见证人区块能被绝对多数的第r+1轮的见证人可见,那么他就是知名见证人。
每个节点都可以在本地通过虚拟投票的拜占庭协议来决定某见证人区块是否是知名见证人。每个r+1轮的见证人区块都会对某第r轮见证人区块进行投票;而第r+2轮的某一见证人会对第r+1轮的投票进行计票,即第r+2轮的见证人会从自己可以强见到的第r+1轮见证人那里收集投票结果。一旦某个投票结果(Yes or No)的计票数目超过绝大多数,见证人就可以决定出投票的结果(decide),就算达成了共识。
这里可能是算法中最不容易理解的地方,因为跨越了三代人的恩怨情仇。。。再简单理下:某个第一代先祖是否知名,必须由第二代先祖来投票他们是否可见第一代祖先,而具体的计票则由第三代先祖进行,第三代先祖肯定是可以强见绝对多数的第二代先祖的(参看创建轮次的定义),所以第三代先祖可以看到并记录下第二代先祖的投票,并且决定投票结果。
并且文中有理论证明,任何一个第三代先祖如果能对投票结果(Yes or No)做出决定,那么这个结果就是全网的结论,因为该轮中其他其他先祖也保证会做出相同的决定。
如果这一轮的见证人没发做出决定(没有任何结果超过绝对多数),那么则会继续交由下一代先祖来计票做决定,直到某轮某个先祖得出明确的结果。文中还有另一理论证明,只要每十轮增加一个随机轮(Coin round),投票肯定终究能完成。在随机轮中,见证者不会做出任何决定,如果见证人收集到了绝对多数的结果,他会根绝结果进行附议投票,否则,见证人则根据自己的数字签名进行随机投票。
在正常情况下,大部分的区块并非见证人区块,所以对于这些区块都不会举行上述的选举知名见证人的投票。而且大部分见证人会在第一轮投票中被一致通过或否决。所以大部分的选举投票不会耗时太过漫长。
此外,一旦所有知名见证人被确定下来,整个网络里的区块顺序(所谓公平性)也就能被更快更容易被推导出来。
确定区块顺序这里引入了接受轮次(received round)的概念,每个区块除了创建轮次外还有接受轮次,第r轮(创建轮次)中所有的知名见证者可见的任何普通区块都会被赋予第r轮的接受轮次。如果有的普通区块没有被所有知名可见证者看到,则它的接受轮次未定,而且肯定会比r更晚。
在确定了接受轮次后,则对所有区块做排序,先按照接受轮次从低到高排,一样的话按照时间戳从早到晚再排,如果还一样的话,则按照区块的签名与某随机数异或出来的结果来排序(将该轮中所有知名见证者的签名进行异或可得到该随机数),这样得出的顺序被称作共识顺序(Consensus order)。
将上述各个操作结合在一起,便是完整的Hashgraph共识算法:
每个节点都在试图随机找到其他节点把自己所知八卦给对方,
每个节点同时也在接受其他节点更新过来的八卦,接受方节点需要额外进行一系列的运算,包括:
接受和处理接收的八卦信息
创建一个新的区块,并且指向自己的最后区块和八卦来源节点的最后区块
对所有已知的区块分配创建轮次,并确定区块是否是该轮次内的见证人区块
对所有已知的见证人区块进行选举投票,计算出是知名见证人
通过知名见证人,确定所有区块的共识顺序
之后白皮书里有很大篇幅对这个共识算法下的系统可以达成拜占庭容错做了很多论证,这里就不再赘述。
总的来说,Hashgraph的立意很高,想法也很新颖,从异步BFT共识的研究上开拓了区块链实现的视野和边疆。前文提到过BFT的模型设置过于悲观和严格,但是公链环境可能就是那么的恶劣,所以Hashgraph这样探索BFT应用到公链的方向和决心是值得肯定的,而且它确实成功的提出了可行的方案。
Hashgraph和Algorand通过从不同角度改良了BFT应用的场景和条件来使得BFT共识可以被应用到公链系统中,可算用心良苦。它们一个是通过八卦传播散列图以及基于散列图做虚拟投票将传统共识所需的瞬时通信要求降到了最低,并且保证了本地计算的高效性,另一个通过安全地舒缩参与到BFT共识节点的数量来把问题划归到BFT擅长的领域,可谓异曲同工。相比较来说,Alogrand的思路更加直观和简单,一般人直觉上可能都能想到这个办法(虽然无法给出完整的方案和数学论证),Hashgraph的思路则更为曲折,引入了很多概念来解释算法,相对来说更晦涩些,虽然相当的理性。
另外Hashgraph这套算法和专利已经成功运用到了很多2B的系统中,但是异步共识是否可以真的在大型公链环境下应用成功,还是一个未知数。最新的Hashgraph公开分布式账本(所谓“公链”)的商业介绍上说他们会切换到POS,就像上文提到过的那样。并且还支持DOPS,可以让不跑节点的coin拥有者选择代理人节点,分享收益。感觉它的未来还是值得期待的。
转载于:
转载月