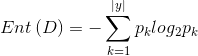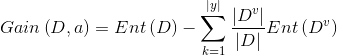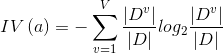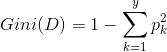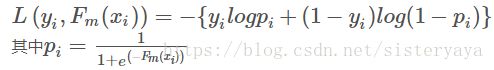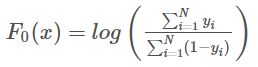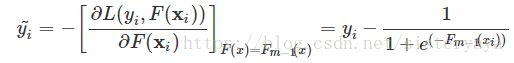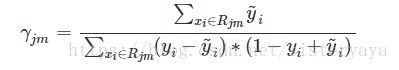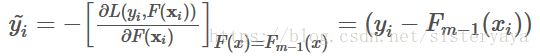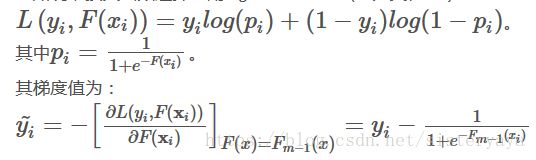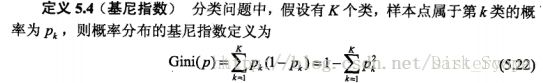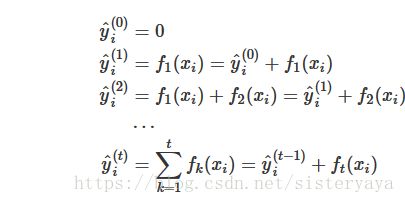机器学习（三）树模型
机器学习（一）LR
机器学习（二）SVM
机器学习（三）树模型
机器学习（四）聚类
机器学习（三）树模型
目录
二、树模型
1、ID3
2、C4.5
3、CART树
（1）算法步骤
（2）举例
（3）参考链接
连续值处理
缺失值的处理
剪枝
集成学习
Boosting：
Bagging：
Stacking：
4、RF
（1）随机性
（2）特征选择：
（3）特征重要性
（4）算法步骤
（5）优缺点
5、GBDT
GBDT—分类树
GBDT—回归树
（1）特征选择
（2）GBDT是如何衡量特征的重要性的
（3）GBDT如何构建新的特征？
（4）正则化
（5）优缺点
6、Xgboost
（1）泰勒二级展开
（2）正则项
（3）shrinkage（缩减）
（4）叶子节点的分裂
（5）并行
（6）稀疏数据缺失值的处理
（7）优点
（8）参考链接：
7、LightGBM
（1）LightGBM的leaf-wise的生长策略
（2）直方图做差加速
（3）支持类别特征
二、树模型
分为单棵决策树和集成树；
决策树的生成就是递归地构建二叉决策树的过程，对回归树用平方误差最小化准则，对分类树用基尼指数最小化准则，进行特征选择，生成二叉树；分枝时穷举每一个feature的每个阈值找最好的分割点
1、ID3
多叉树；树的分裂以信息增益为划分标准，只能处理离散数据；对于连续数据得先离散化；偏向于取值较多的特征;
离散化方法：等距（取值范围均匀划成n等份，每份的间距相等）、等频（均匀分为n等份，每份内包含的观察点数相同）、优化方法（卡方检验、信息增益等）；
信息熵：度量样本集合纯度的一种指标；假定当前样本集合D 中 
类样本所占比例
，则根节点D的信息熵为：
,
信息增益：用属性a对样本集D进行划分所获得的“信息增益”；a中有v个可能取值，
为属性a中取值是v的样本集合数；根节点的信息增益减去 属性a下的可能取值的信息熵之和：
,
- 信息熵越小，纯度越高；
- 信息增益越大，意味着使用属性 a 来进行划分所获得的的“纯度提升”越大；
- 取值越多，信息增益越大，如按编号划分，每个节点仅包含一个样本，纯度已达最大，这样的决策树不具有泛化能力，无法对新样本进行有效预测；
- 所以，信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好带来的不利影响，出现了“信息增益率”；
2、C4.5
多叉树；既能处理离散数据，也能处理连续数据；每次分裂节点时，需对特征值进行排序，再枚举所有的可能分割点；分割点的值为相邻两个值的均值；皆以信息增益率为划分标准；
信息增益率：
,
其中：
,
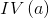称为a的“固有值”，a的可能取值数目越多（即V越大），则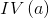的值通常会越大；- 信息率准则对可能取值较少的属性有所偏好；因此C4.5并不是直接选择信息增益率大的候选划分属性，而是采用了一种启发式：
- 启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率高的；
3、CART树
二叉树；
分类树：以两节点最小gini指数为分裂标准；输出为最终节点内类别较多的那一类为预测结果；
回归树：两个节点的最小均方误差（MSE)为标准；最终节点内的均值为最终输出；
属性 a 的基尼指数定义为：
，其中基尼值：
，Gini(D)值越小，数据集D纯度越高；
（1）算法步骤
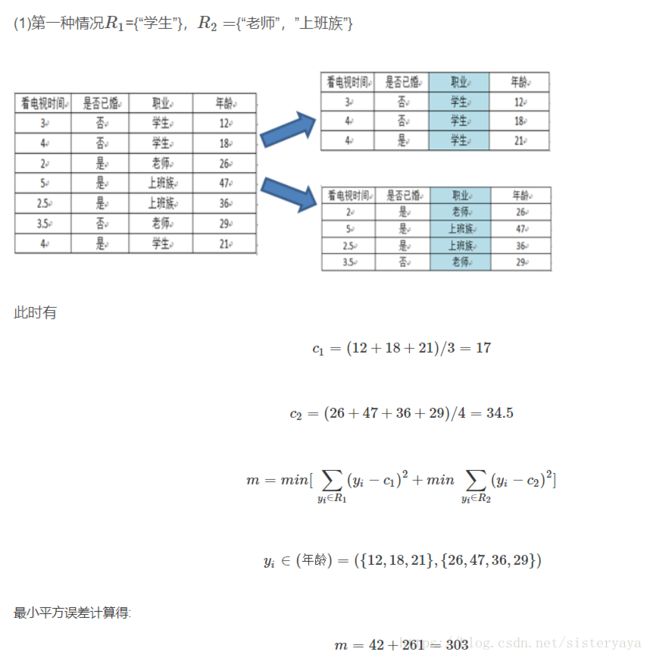
总结（回归树）：递归的将样本集划分为两个区域，并通过遍历属性和属性下的候选切分点（子区域的中间值），找到使均方误差最小的切分属性和切分点，以结点内的均值为输出值，构建二叉树；
（2）举例
1）回归树——以职业为属性预测年龄
2）分类树——以职业为属性预测是否已婚
（3）参考链接
https://www.jianshu.com/p/b90a9ce05b28
https://blog.csdn.net/gzj_1101/article/details/78355234
-
连续值处理
将值从小到大排序，基于划分点 t 将数据划分为两个区域，每个区域的中间值作为候选划分点；其余同离散属性的划分方法；
-
缺失值的处理
先对非缺失数据进行统计，对其进行正常划分，然后把含缺失值的样本以不同的概率划分到不同的子结点中去；具体方法是赋予权重，初始值都为1，进入不同节点后进行调整（调整后的权重：该属性可能取值为v的样本数/该属性不含缺失值的总样本数）；
-
剪枝
目的：降低过拟合风险；
预剪枝：在决策树生成过程中，对每个结点在划分前先进行预估，若划分后不能带来泛化性能的提升，则停止划分；
后剪枝：tree完全生长后，通过对结点划分前后错误率的评估，对不良子树进行剪枝；
如何评估？留一部分验证集，由验证集精度进行取舍；
后剪枝之悲观剪枝：根据剪枝前后的错误率来判定子树的修建；引入了误判因子来抵消出现的偏倚（偏倚是指一切测量值对真值的偏离），当子树的误判个数大过对应叶节点的误判个数一个标准差之后，就决定剪枝；
悲观剪枝准确度比较高，但仍会出现过度剪枝的情况；
参考链接
集成学习
通过构建多个学习器来完成学习任务。集成学习有两个流派，一个是boosting派系，它的特点是各个弱学习器之间有依赖关系。另一种是bagging流派，它的特点是各个弱学习器之间没有依赖关系，可以并行拟合；
Boosting：
将弱学习器提升为强学习器的算法。先从训练集训练一个基学习器，再根据基学习器的表现对训练样本的分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分部训练下一个基学习器；重复，如果训练的基学习器不满足条件，舍去，重新训练，如此直到训练T个学习器后，进行加权结合；
方法：“重采样法”（分上采样和下采样，区分的依据是重新采样的时候新采样率和原采样率的大小的比较，新大于旧为上采样，反之下采样；对于一个样值序列间隔几个样值取样一次，这样得到新序列就是原序列的下采样，上采样就是增加样本，下采样就是抽取样本）；关注降低偏差；
代表：AdaBoost：通过更新权重来调整样本分布，其中，由最小指数损失函数来更新分类器的权重；
具体：首先初始化样本权值分布（1/m 为样本数的倒数），基于该分布训练第一个基分类器，此后迭代地生成及分类器 
和 的权重 
，当及基分类器 基于分布 
产生后，该分类器的权重应使得 
最小化指数损失函数；（权重是通过对指数函数求导为 0，推导而来的；）详细见西瓜书；
弱分类器是基于分布 来训练的，且针对 的分类误差应小于0.5；弱条件不满足，则当前基学习器即被抛弃，且学习过程停止，这种情况下，初始设置的学习轮数 T 未满足，可能导致最终集成的效果不佳；
可采用“重采样法”，可避免训练过程过早停止，即在抛弃不满足条件的当前学习器之后，可根据当前分布重新对训练样本进行采样，再基于新的采样结果重新训练基学习器；
【西瓜书上说，Boosting算法要求基学习器能对特定分布进行学习，这可通过“重赋权法”实施，即在训练过程的每一轮中，根据样本分布为每个训练样本重新赋予一个权重，对于无法接受带全样本的基学习器算法，则可通过“重采样法”；】
缺点：如果采样出的每个子集都完全不同，则每个基学习器只用到了一小部分数据，不足以进行有效学习，这显然无法确保产生出了比较好的基学习器；为解决这个问题，我们可以考虑用相互有交叠的采样子集bagging；
Bagging：
有放回的采样训练T个基学习器，在进行组合；每个基学习器只用了一部分数据，另一部分可用来泛化性能检验；
方法：有放回的采样；关注降低方差；
分类：投票；
回归：平均；
Stacking：
代表：GBDT+LR；
第一层：
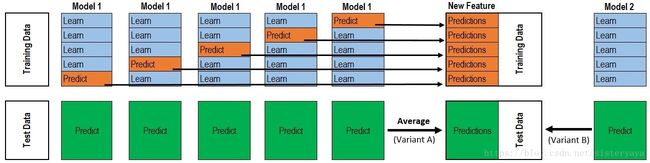
样本数10000，num_trees=30，testSet=500，num_leafs = 64，对训练数据五折交叉验证，则trainSet = 8000，validSet=2000，用trainSet训练模型model1，对validSet预测输出p1（2000*1），同时对testSet进行预测输出t1（500*1）；五折后，将验证集的所有预测值[p1,p2,p3,p4,p5]T 转为一列10000*1（1w行，1列）；测试集的输出按行取平均（500*1）；
若第一层还会有其他 Model 的，比如 Model 2，同样的走一遍， 我们有可以得到 10000 X 1 (p2) 和 500 X 1 (t2) 列预测值。
这样吧，假设你第一层有3个模型，这样你就会得到：
来自 5-fold 的预测值矩阵 10000 X 3，（p1，p2，p3） 和 来自 testSet 预测值矩阵 500 X 3， （t1, t2, t3）。
注：对于GBDT+LR，因为30颗树，所以输出为10000*30，每棵树输出样本所在的结点的索引位置；
第二层：
来自 5-fold 的预测值矩阵 10000X 3 作为你的 trainSet，训练第二层的模型
来自 testSet 预测值矩阵 500 X 3 就是你的 testSet，用训练好的模型来预测他们吧。
注：对于GBDT+LR，
#pred_leaf=True，输出为矩阵，每个值为每棵树的叶子结点的索引值
y_pred = gbm.predict(X_train, pred_leaf=True)我们需要将每棵树的特征进行one-hot处理，如前面所说，假设第一棵树落在43号叶子结点上，那我们需要建立一个64维的向量，除43维之外全部都是0。因此用于LR训练的特征维数共num_trees * num_leaves，测试集也做同样处理；再放进LR中训练；
scikit-learn中apply()函数：每个样本都输出一个预测向量，指出了在每棵子树上的预测节点。
总结：
- 第一层对原始数据进行5折交叉验证，用每一折训练出的model对验证集、测试集分别进行预测，所有验证集的预测值作为下一层的训练样本用于训练新的model，5份测试集的预测值取均值作为第二层的测试样本，用于预测；
- LR是线性模型，需要大量的特征工程来增加模型的学习能力
- 为什么要用集成的决策树模型，而不是单棵？一棵树的表达能力很弱，不足以表达多个有区分度的线性特征，多棵树的表达能力更强一些，可以更好地发现有效的特征和特征组合；
- 为什么用GBDT而非RF：RF也是多棵树，但从效果上证明不如GBDT;且GBDT前面的树，特征分裂主要体现对多数样本有区分度的特征；后面的树，主要体现的是经过前N颗树，残差仍然很大的少数样本；优先选用在整体上有区分度的特征，在选用针对少数样本有区分度的特征，思路更加合理；
- GBDT本身是不能产生特征的，但是我们可以利用GBDT产生特征的组合，逻辑回归一般用于处理线性可分的数据，可通过组合不同的特征，让其处理线性不可分的数据，增强 lr 对非线性分布的拟合能力。
注：关于高维离散数据，非线性模型和非线性模型的比较，对于tree，树模型的惩罚项通常是叶子节点数和深度，只需要一个结点就可以完美分割大量非0样本和较少0值样本，惩罚项很小，而LR等线性模型的自带的正则是对权重的惩罚，权重越大，惩罚越大，通过压缩权重使权重不会太大；所以对高维稀疏特征，线性模型比非线性模型好；带正则的线性模型比较不容易对稀疏特征过拟合；
来源：推荐系统遇上深度学习(十)--GBDT+LR融合方案实战
参考链接：
推荐系统遇上深度学习(十)--GBDT+LR融合方案实战
Kaggle机器学习之模型融合（stacking）心得
4、RF
（1）随机性
（自样本扰动；自属性扰动）
- 随机选择样本;
- 随机选择特征（若有一个强特征（与标签强相关），那每棵决策树都选到它，输出都一样，所以要随机）；随即特征个数一般为总特征数 M 的均方根sqrt（M/2)；
细瓜书上说：对基决策树的每个结点，先从该每个结点（d个属性）的属性集合中随机选择一个包含K个属性的子集：再从这个子集中选择最优属性用于划分，其中
，
（2）特征选择：
ID3 在选则节点特征时会遍历所有特征，计算其信息增益，选增益大的作为分裂节点，偏向于划分属性多的特征如ID类；
C4.5是信息增益率，在ID3的基础上增加了抑制，先选择信息增益大于均值的，再在此基础上选择信息增益率大的；
（3）特征重要性
1）RF 中的每棵树的建立用的是部分数据，那用剩下的数据（袋外数据OOB）计算误差（分错的样本量/样本总量（袋外数据））errOOB1；
2） 随机地对袋外数据OOB所有样本的特征X加入噪声干扰(就可以随机的改变样本在特征X处的值)，再次计算它的袋外数据误差,记为errOOB2；
3）假设随机森林中有Ntree棵树，那么对于特征X的重要性 = ∑(errOOB2-errOOB1)/Ntree，之所以可以用这个表达式来作为相应特征的重要性的度量值是因为：若给某个特征随机加入噪声之后,袋外的准确率大幅度降低，则说明这个特征对于样本的分类结果影响很大，也就是说它的重要程度比较高；
（4）算法步骤
输入为样本集D={(x1,y1),(x2,y2),...(xm,ym)}，弱分类器迭代次数T。输出为最终的强分类器f(x):
- 算法步骤：
对于t=1,2...,T:
a)对训练集进行第t次随机采样，共采集m次，得到包含m个样本的采样集Dm
b)用采样集Dm训练第m个决策树模型Gm(x)，在训练决策树模型的节点的时候， 在节点上所有的样本特征中选择一部分样本特征，在这些随机选择的部分样本特征中选择一个最优的特征来做决策树的左右子树划分
- 结合策略：
分类：投票法；则T个弱学习器投出最多票数的类别或者类别之一为最终类别。（各基学习器性能相差较大时用加权平均法。）
回归：简单平均法；T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。
（5）优缺点
优点：可并行处理，训练速度快；由于采用了随机采样，训练出的模型的方差小，泛化能力强；可输出特征重要性；
缺点：取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果；对于回归，每次迭代需要遍历所有特征计算信息增益/信息增益率/gini指数，时间开销大；
5、GBDT
GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。这就是Gradient Boosting在GBDT中的意义。
在GBDT的迭代中，假设我们前一轮迭代得到的强学习器是ft−1(x), 损失函数是L(y,ft−1(x)), 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器ht(x)，让本轮的损失损失L(y,ft(x)=L(y,ft−1(x)+ht(x))最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。
公式推导：https://www.cnblogs.com/pinard/p/6140514.html
1） Gradient boosting思想是迭代生多个（M个）弱的模型，然后将每个弱模型的预测结果相加，后面的模型Fm+1(x)基于前面学习模型的Fm(x)的效果生成的；
弱分类器一般会选择CART 回归树；boosting算法是在迭代的每一步构建弱学习器来弥补原有模型的不足；GBDT限定了只能用CART树；
GBDT通过多轮迭代,每轮迭代产生一个弱分类器，每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单，并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度；
用残差更新每个样本的目标值：叶子节点的均值作为落到该叶子节点的样本的预测值，使用目标值减去预测值，得到该样本的残差，作为下一棵树的训练目标；
解决两个问题：
一、每轮学习中，如何改变训练数据的权值或者概率分布：
通过拟合损失函数 的负梯度值；
二、若何将若学习器组合成一个强分类器的：
用CART回归树；
2）为什么用负梯度下降？
Gradient Boosting是一种Boosting的方法，它主要的思想是，每一次建立模型是在之前建立模型损失函数的梯度下降方向，如果我们的模型能够让损失函数持续的下降，则说明我们的模型在不停的改进，而最好的方式就是让损失函数在其梯度方向上下降。容易局部最优；
Gradient boost则是通过每次迭代的时候构建一个沿梯度下降最快的方向的学习器来弥补模型的不足。多分类算法步骤如下，训练F0-Fm共m个基学习器，沿着梯度下降的方向不断更新叶子节点值 r、估计值 F（x）；
多分类：
算法步骤： https://blog.csdn.net/w28971023/article/details/43704775
3）Adaboost
AdaBoost的目的是通过构建弱学习器的线性组合来得到最终分类器；
用前向分布算法求解的思想是： 因为学习的是加法模型，那如果能够从前向后，每一步只学习一个基函数及其系数，然后逐步逼近优化目标，那么就可以简化优化的复杂度。
Adaboost也是另一种boost方法，它按分类对错，分配不同的weight，计算cost function时使用这些weight，从而让“错分的样本权重越来越大，使它们更被重视”。即通过给被已有模型预测错误的样本更高的权重，使得先前被学习错误的样本可以在后续的训练中得到更高的关注来弥补原有模型的不足；对一份数据，建立M个模型（比如分类），可以想象得到，程序越往后执行，训练出的模型就越会在意那些容易分错（权重高）的点。当全部的程序执行完后，会得到M个模型，分别对应上图的y1(x)…yM(x)，通过加权的方式组合成一个最终的模型YM(x)。
经典的AdaBoost算法只能处理采用指数损失函数的二分类学习任务，而梯度提升方法通过设置不同的可微损失函数可以处理各类学习任务（多分类、回归、Ranking等），应用范围大大扩展。AdaBoost算法对异常点（outlier）比较敏感。
GBDT—分类树
如何分类？ 通过迭代，更新 预测值 使 误差函数 L 越来越小
k分类：每次同时训练k棵树；
损失函数使用LR的logloss，则损失函数为：
，
初始化F（x），即正样本的个数/负样本的个数，取log：
然后对其求一阶导，得到负梯度值：
再找最佳切分点：遍历所有特征及其所有可能切分点，选最小均方误差的（j，m）值作为最优切分点，以特征 j，阈值m将样本划分为两个区域 R1 和 R2；即两个叶子结点
再求每个区域即叶子结点值：
若为误差函数为最小均方误差，则叶子节点值为均值；
更新预测值 F（x），这里同样也用shrinkage，每完成一次迭代，叶子节点的权重都乘以一个缩减因子，即乘一个学习率 η，以减少每棵树的影响：根节点分为两个叶子节点，叶子节点的值时唯一的，所以每个叶子节点上求出的F（x）值都一样，即为每棵树的输出：
再进行下一轮迭代，建第二棵树；
最后的预测 F(x) 值通过sigmoid函数转化为概率：为正样本的概率为：
Fm(x)的值可负可正，sigmoid函数的输入为（负无穷，正无穷），输出在0~1之间，满足概率分布为0~1的要求；它是个单调上升函数，具有连续性；所用sigmoid函数来求输出概率。算法步骤总结如下：
注意求负梯度时，每次迭代
的值都为原始样本值；
若误差函数为最小均方误差（mse），因一阶导数不同使叶子节点值求法不同，其余类似，
F0(x)=y¯，y¯为样本真实值的平均值；回归问题: MSE
GBDT—回归树
算法流程：
建树的分裂标准不同，预估值的初始化方法也不一样；分裂标准是MSE时：
第一步：初始化
为样本真实值的均值；
第三步：求每个样本的负梯度值 
：
1、损失函数为MSE时：
梯度值为：
2、损失函数为logistic loss时（二分类）：
第四步：以负梯度值为目标，拟合一棵树：找使均方误差最小的特征及它的最优切分点，将样本区域划分为不同的子区域；
其目的就是为了求一个最优的基分类器。对于不同的基分类器有不同的寻找，比如，对于决策树，寻找一个最优的树的过程其实依靠的就是启发式的分裂准则；切分点将样本区域划分为不同的子区域；
其想表达的是以{y~i,xi}N1为训练数据，拟合一颗回归树，最终得到叶子节点的区域；
第五步：求叶子结点的取值，即叶子结点的输出是多少；
注：无论哪一棵树，
一直都是数据的原始值；
第六步：求得基分类器后，利用加法模型，更新出下一个模型；
注：有 m 棵树时，
即为预测结果；
参考链接：
机器学习算法GBDT的面试要点总结-上篇
GBDT理解二三事
分类树：GBDT原理与Sklearn源码分析-分类篇
GBDT原理与Sklearn源码分析-回归篇
多分类：GBDT原理与实践-多分类篇
（1）特征选择
弱学习器用的是CART回归树；CART tree生成过程：寻找一个特征j作为节点，特征j下的值m为切分点，大于m的为一类，小于m的为另一类；
1）回归树，分支时，穷举每一个feature的阈值，找到最好的分割点；损失函数一般用均方误差；
2）分类树：输出的是属于某一类的概率值；分裂方法同回归树；损失函数一般用 LR算法中的 logloss；
（2）GBDT是如何衡量特征的重要性的
计算所有的非叶子节点在分裂时加权不纯度的减少，减少得越多说明特征越重要。GINI越小，数据越纯；
不纯度的减少实际上就是该节点此次分裂的收益，因此我们也可以这样理解，节点分裂时收益越大，该节点对应的特征的重要度越高。
总结：特征 j 的重要性即，每棵树中与之相关的叶子结点分裂之后平方损失的减少值之和，再对所有树求均值；
（3）GBDT如何构建新的特征？
GBDT本身是不能产生特征的，但是我们可以利用GBDT产生特征的组合，逻辑回归一般用于处理线性可分的数据，可通过组合不同的特征，让其处理线性不可分的数据，增强 lr 对非线性分布的拟合能力。
假如有两棵树，一个样本 x 进来，在第一棵树（共三个叶子节点）落到第二个叶子节点上，在第二棵树（共两个叶子节点）落到第1个叶子节点上，那我们可以构建一个五维的特征向量（0/1)，[0,1,0,1,0]，1为每棵树上叶子节点的位置，其余为0；
于是对于该样本，我们可以得到一个向量[0,1,0,1,0] 作为该样本的组合特征，和原来的特征一起输入到逻辑回归当中进行训练。实验证明这样会得到比较显著的效果提升。
参考链接：https://www.cnblogs.com/ModifyRong/p/7744987.html
（4）正则化
1）加学习率
2）子采样：因为GBDT是不放回的采样，子采样，可防止过拟合，但会增加样本拟合的偏差；使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样，程序可以通过采样分发到不同的任务去做boosting的迭代过程，最后形成新树，从而减少弱学习器难以并行学习的弱点。
子采样，即用一部分样本按行并行化，将样本按行分成N份，分别在N个节点上做计算；
（5）优缺点
GBDT主要的优点有：
1) 可以灵活处理各种类型的数据，包括连续值和离散值。
2) 在相对少的调参时间情况下，预测的准备率也可以比较高。这个是相对SVM来说的。
3）使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
GBDT的主要缺点有：
1)由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
6、Xgboost
XGBoost中文文档
一次添加一棵新的树。 我们通过 y^(t)i 来关注步骤 t 的预测值，并添加一个优化我们目标，
这个定义的一个重要优点是它只依赖于 gi 和 hi 。这就是 xgboost 如何支持自定义损失函数。 我们可以使用完全相同的使用 gi 和 hi 作为输入的 solver（求解器）来对每个损失函数进行优化，包括 logistic regression， weighted logistic regression。
正则项与树的叶子节点的数量T和叶子节点的值有关，正则项用于控制模型的复杂度；
结构分数：
最后一个式子可以度量一棵树到底有多好，即结构分数；
（1）泰勒二级展开
传统GBDT只用到误差函数的一阶导数信息，XGBOOST对代价函数进行了二级泰勒展开；最后的式子可看出优化目标只用到了一阶导数gi和二阶导数hi；
摘自其他博客：由于gbdt只用到了一阶信息，如果按照公式推导，相当于loss只进行了一阶泰勒展开。在没有复杂度项的情况下，无法确定步长，所以只能用常数步长根据一阶梯度方向去逼近。这就是牛顿下降法和梯度下降法的区别。由于二阶展开用二次函数去逼近函数，所以可以利用二阶信息确定更新步长，比只利用一阶信息的gdbt用更少的迭代获得更好的效果。
总：可自定义损失函数，计算方便，进行二级泰勒展开；
（2）正则项
控制树的复杂度；正则项包含树的叶子节点的数目，以及每个叶子节点的输出分数score的L2模的平方和；从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合；
（3）shrinkage（缩减）
即学习率；每完成一次迭代，叶子节点的权重都乘以一个缩减因子，以减少每棵树的影响；GBDT也有；
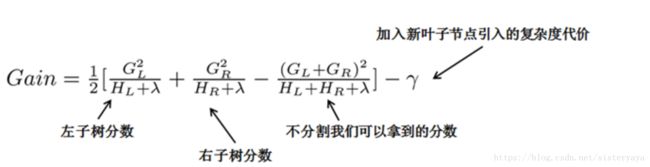
（4）叶子节点的分裂
每次分裂，计算分裂的增益（loss function的降低量）只需要关注打算分裂的那个节点的样本节点的分裂方式，同一层可并行分裂；
分裂结点处通过结构打分和分割损失动态生长。结构分数代替了回归树的误差平方和。
如果增益小于 
，我们最好不要添加那个分支；这正是基于树模型的 pruning（剪枝） 技术！
预排序：我们通常要寻找一个最佳的分割，为了有效的做到这一点，我们把所有的实例按照顺序排序，然后从左到右的扫描就足以计算所有的拆分解决方案的结构得分，我们可以有效地找到最佳的拆分；
1）、贪心算法
2）、近似算法
对于一个特征，如“销量”，取值较多，不能枚举所有的切割点，xgboost先对特征值预排序，保存为block结构，每次分裂时再提取出来，使算法高效；将样本分成几个区间，满足(特征值小于分位点z的每个间隔的样本的hi（二阶导）之和/总样本的hi之和）为某个百分比ϵ（我这个是近似的说法），那么可以一共分成大约1/ϵ个分裂点。
3）、直方图算法
直方图算法用于高效的生成最优切割点；
遍历每个特征，对每个特征的值进行预排序，分区间存储在不同的桶中；对每个特征创建一个直方图，里面记录了不同桶里的特征值的二阶梯度hi之和以及样本数；详细可参考lighgbm的直方图做差加速；
统计每个特征里面点的权值确定候选切割点(理解为按照一定顺序排成直方图相邻候选点不超过阈值控制直方图每个宽度) 。
目标函数可转化为带权的形式：
根据特征分布的百分比提取特征？其中sk1是特征k的取值中最小的值xik，其中skl是特征k的取值中最大的值xik，这是分位数缩略图的要求需要保留原序列中的最小值和最大值。ϵ是一个近似比例，或者说是扫描步幅。可以理解为在特征K的取值范围上，按照步幅ϵ挑选出特征K的取值候选点，组成候选点集。起初是从sk1起，每次增加ϵ∗(skl−sk1)作为候选点，加入到候选集中。如此计算的话，这意味着大约是 1/ϵ个候选点。
其中获取某个特征K的候选切割点的方式叫proposal.主要有两种proposal方式:global proposal和local proposal.
此时特征k的取值中最小的值xik和特征k的取值中最大的值xik来自的数据集Dk，对于Dk的数据集有两种定义，一种是一开始选好，然后每次树切分都不变，也就是说是在总体样本里选最大值skl和最小值sk1，这就是我们之前定义的global proposal。另外一种是树每次确定好切分点的分割后样本也需要进行分割，最大值skl和最小值sk1来自子树的样本集Dk，这就是local proposal。
参考链接：
论文阅读-XGBoost: A Scalable Tree Boosting System -论文的概述
决策树相关算法——XGBoost原理分析及实例实现(二) -分位点的讲解
（5）并行
支持并行化处理。xgboost的并行是在特征粒度上的，在训练之前，预先对特征进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行，即在不同的特征属性上采用多线程并行方式寻找最佳分割点。
分裂结点特征分割点选取使用了近似算法-可并行的近似直方图算法。可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。用于加速和减小内存消耗。直方图加速是LightGBM的。。。
同层级节点可并行。具体的对于某个节点，节点内选择最佳分裂点，候选分裂点计算增益用多线程并行；
（6）稀疏数据缺失值的处理
XGBoost还特别设计了针对稀疏数据的算法，
假设样本的第i个特征缺失时，无法利用该特征对样本进行划分，这里的做法是将该样本默认地分到指定的子节点，至于具体地分到哪个节点还需要某算法来计算，
算法的主要思想是，分别假设特征缺失的样本属于右子树和左子树，而且只在不缺失的样本上迭代，分别计算缺失样本属于右子树和左子树的增益，选择增益最大的方向为缺失数据的默认方向（咋一看如果缺失情况为3个样本，那么划分的组合方式岂不是有8种？指数级可能性啊，仔细一看，应该是在不缺失样本情况下分裂后（有大神的请确认或者修正），把第一个缺失样本放左边计算下loss function和放右边进行比较，同样对付第二个、第三个…缺失样本，这么看来又是可以并行的？？）；
（7）优点
- 传统的GBDT以CART树为基分类器，xgboost还支持线性分类器，这个时候xgboost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。 —可以通过booster [default=gbtree]设置参数:gbtree: tree-based models/gblinear: linear models；
- 对目标函数进行Taylor二级展开，支持自定义损失函数；
- 正则项：目标函数为训练损失函数+正则项，正则项包含了树的叶子结点树、每个叶子的结点输出的分数的L2模的平方和，用于控制树的复杂度，防止过拟合；
- shinkage：缩减类似于学习率，每棵树建好之后乘以一个学习率，以减少每棵树的影响，为后面的树提供优化空间；
- 列采样：列特征抽样，同RF？
- 划分点查找算法：pre-sorted
- 处理缺失值：稀疏感知算法
- 交叉验证，方便选择最好的参数，early stop，比如你发现30棵树预测已经很好了，不用进一步学习残差了，那么停止建树；
- 支持并行化：特征粒度上的；
- 定义结构分数：分裂结点处通过结构打分和分割损失动态生长。结构分数代替了回归树的误差平方和。
（8）参考链接：
公式推导： https://blog.csdn.net/guoxinian/article/details/79243307
原理细节： https://blog.csdn.net/github_38414650/article/details/76061893
xgboost入门与实战（原理篇）
7、LightGBM
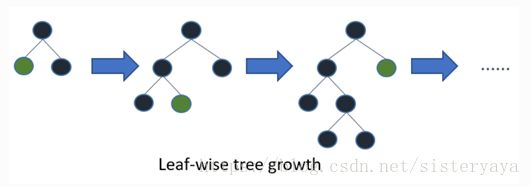
（1）LightGBM的leaf-wise的生长策略
它摒弃了现在大部分GBDT使用的按层生长（level-wise）的决策树生长策略。level-wise过一次数据可以同时分裂同一层的叶子，容易进行多线程优化，也好控制模型复杂度，不容易过拟合。但实际上level-wise是一种低效的算法，因为它不加区分的对待同一层的叶子，带来了很多没必要的开销，因为实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。
LightGBM 使用带有深度限制的按叶子生长（leaf-wise）的策略.
Leaf-wise则是一种更为高效的策略，每次从当前所有叶子中，找到分裂增益最大的一个叶子，然后分裂，如此循环。因此同Level-wise相比，在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树，产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合。
（2）直方图做差加速
其思想是将连续的浮点特征离散成k个离散值，并构造宽度为k的Histogram。然后遍历训练数据，统计每个离散值在直方图中的累计统计量。在进行特征选择时，只需要根据直方图的离散值，遍历寻找最优的分割点。
直方图优化算法需要在训练前，对特征值预排序，然后对每个特征的取值做个分段函数，将所有样本在该特征上的取值划分到某一段（bin）中。最终把特征取值从连续值转化成了离散值。即分区间统计二级梯度hi的和及样本数；
首先，对于当前模型的每个叶子节点，需要遍历所有的特征，来找到增益最大的特征及其划分值，以此来分裂该叶子节点。在第二个for循环中，
上面第三步中涉及到了lightgbm的一个优化——Histogram（直方图）做差加速。一个容易观察到的现象：一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。通常构造直方图，需要遍历该叶子上的所有数据，但直方图做差仅需遍历直方图的k个容器。利用这个方法，LightGBM 可以在构造一个叶子的直方图后，可以用非常微小的代价得到它兄弟叶子的直方图，在速度上可以提升一倍。
总结：对连续特征，先预排序，然后离散化为k的区间，放到不同的bin中，对每个bin统计样本数和二级梯度之和，然后用一个直方图来存储所有的bin；叶子分裂时，遍历所有bin找最优分割点，先分别累加左边的bin里面的两个值，再用父结点减去左边的就得到了右边结点的样本数和二级梯度和，再计算增益，增益大的作为最优分裂特征和分割点；
（3）支持类别特征
可直接输入类别特征，无需进行one-hot编码，减少了时间和空间的开销；
我们通常将类别特征转化为 one-hot coding。 然而，对于学习树来说这不是个好的解决方案。 原因是，对于一个基数较大的类别特征，学习树会生长的非常不平衡，并且需要非常深的深度才能来达到较好的准确率。
事实上，最好的解决方案是将类别特征划分为两个子集，总共有 2^(k-1) - 1 种可能的划分 但是对于回归树 [7] 有个有效的解决方案。为了寻找最优的划分需要大约 k * log(k) .
基本的思想是根据训练目标的相关性对类别进行重排序。 更具体的说，根据累加值(sum_gradient / sum_hessian)重新对（类别特征的）直方图进行排序，然后在排好序的直方图中寻找最好的分割点。
（end）
欢迎大家指错，不尽感谢~
【本系列是根据网上资源和个人见解总结而来的，如需转载请备注原文链接。】