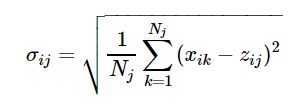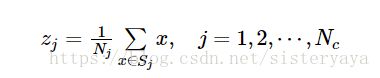机器学习（四）聚类

机器学习（一）LR

机器学习（二）SVM

机器学习（三）树模型

机器学习（四）聚类

---

机器学习（四）聚类

目录

机器学习（四）聚类

1、k-means算法

（1）初始值

（2）K值

（3）中心点的确定

（4）优点

（5）缺点

2、k_means++

3、ISODATA

 （1）   参数

（2）分裂

（3）缺点

（4）参考链接

4、kernel k-means

5、DBSCAN

6、层次聚类

7、FCM

8、尺度化

参考链接

---

---

1、k-means算法

    K-means是通过迭代来实现的。每次确定K个中心点，计算各节点与中心点的距离（欧氏距离），将离中心点距离最近的节点归到相应的cluster，更新簇心直到收敛；

伪代码：

（1）初始值

    1) 一般是随机生成或在样本空间随机选取，若数据量不太，选使最小目标函数J的聚类作为最后结果;

    2) 遗传算法（GA）;

（2）K值

        1） 一般需人为预先确定，当数据量过大，高维时，难以确定K值；

        2） ISODATA算法：通过类的自动合并和分裂得到较好的K值；基本思想：类别样本数较小时直接去掉；样本数较大，分散程度较大时再分为两个子类；

（3）中心点的确定

    计算簇内所有样本的均值，作为中心点，此时很容易受离群点的影响，使变差过大；均值衡量的是数据集的整体误差，往往会  掩盖数据本身的特性； 

    最终结果： 平方误差和（SSE）最小；各簇内样本点与中心点的误差平方和，所有簇累加；

（4）优点

    确定k的cluster的平方误差最小，当类类区别明显时，效果好；数据量大的时候高效；

（5）缺点

    1）K值和初始值难确定；

    2）对噪声点和离群点敏感；

    3）目标函数容易收敛到局部最优；

2、k_means++

    随机选取一个样本作为第一个簇中心，计算其他样本到中心的距离，距离越大聚为新类的概率就越大，从而确定为下一个簇中心，依次类推，找到k个簇中心；

           概率 =      

    与k-means的本质区别是聚类中心的初始化过程；

3、ISODATA

    该算法能够在聚类过程中根据各个类别包含的实际情况动态调整聚类中心的数目。如果某个类中样本分散程度较大（通过方差  衡量）    并且样本数量较大，则对其进行分裂操作；如果两类别靠得比较近（通过簇类中心的距离衡量），则对它们进行合并操作；

 （1）   参数

    1）只需设定K值范围，即可通过数据实际情况调整 k 值；分裂（簇）-减小簇中心数、合并（簇）-增加簇中心数；

    2）每个类目要求的最小样本数：少于某值不分裂；

    3）标准差阈值：衡量某类别中样本的分散程度，大于某值不分裂；

        

4）两个类别对应聚类中心之间所允许的最小距离dmin：若两簇之间距离小于dmin则合并；

（2）分裂

            

    计算聚类中心 zj ， 各分量的标准差向量σj  。 则将zj 分裂为两个新的聚类中心和，且Nc加1。一类  z1中对应于σjmax的分量加上kσjmax， z2中对应于σjmax的分量减去kσjmax。

（3）缺点

    需设置较多参数，参数也不容易确定；

（4）参考链接

    https://www.cnblogs.com/huadongw/articles/4101306.html

4、kernel k-means

    传统K-means采用欧式距离进行样本间的相似度度量，显然并不是所有的数据集都适用于这种度量方式。

引入支持向量机中的核函数，将样本映射到另一个空间再进行聚类；

5、DBSCAN

    由一个点确定一个 cluster 的方法；    

        基于密度的聚类算法，只要一个区域的密度大于某个阈值，就可加入与之相近的类中；比如：选择点 o1，以o1为中心，半径为r的圆内包含的点的个数为5，大于设定值4，则o为核心点，这5个点为一个簇cluster1；然后选择点o2，若o2不在cluster1 中，且其r范围内点的个数小于5，则不是核心点，跳过，然后选择o3，...，依次遍历所有数据;

        可根据一个点的邻居点来计算空间密度；

优点：可以克服基于距离的算法只能发现“类圆形”的缺点，可以是任何形状，对离群点不敏感；不需要输入K值；

        两个参数：半径ϵ 描述了某一样本的邻域距离阈值，MinPts描述了某一样本的距离为ϵ的邻域中样本个数的阈值。

缺点：计算密度单元的计算复杂度大,需要建立空间索引来降低计算量,对数据维数的伸缩性比较差；高维数据，半径不易确定；不适用密度集中差异大的数据；

应用：地理数据聚类、图像；

延伸：DBTICS：不对参数敏感；

6、层次聚类

    自上而下；距离最小原则；

假设有N个待聚类的样本，对于层次聚类来说（自下而上），基本步骤就是：
1）、（初始化）把每个样本归为一类，计算每两个类之间的距离，也就是样本与样本之间的相似度；
2）、寻找各个类之间距离最近的两个类，把他们归为一类（这样类的总数就少了一个）；
3）、重新计算新生成的这个类与各个旧类之间的相似度；

4）、重复2和3直到所有样本点都归为一类， 或者某个终结条件被满足（比如类之间的相似度小于设定的阈值），则结束。

    进一步，指定一个距离T，就可以得到分类的数目，如下：567为一类，其余为一类；

                            

7、FCM

    模糊C均值聚类（FCM），即众所周知的模糊ISODATA，是用隶属度确定每个数据点属于某个聚类的程度的一种聚类算法。

 

8、尺度化

    若属性具有相同的单位就不需要进行尺度化，若单位不同则需尺度化（化为相同单位）；尺度化会影响聚类效果；

 

 欢迎大家指错，不尽感谢~

【本系列是根据网上资源和个人见解总结而来的，如需转载请备注原文链接。】