三维球体史密斯圆图的发展与理解，史密斯圆图的最新发展

Smith圆图的发展

史密斯圆图简介

史密斯圆图(Smith chart）是一款用于电机与电子工程学的圆图，主要用于传输线的阻抗匹配上。一条传输线(transmission line)的电阻抗力(impedance)会随其长度而改变，要设计一套匹配(matching)的线路，需要通过不少繁复的计算程序，史密斯圆图的特点便是省却一些计算程序。

起源背景：

由菲利普·史密斯(Phillip Smith)于1939年发明，当时他在美国的RCA公司工作。史密斯曾说过，“在我能够使用计算尺的时候，我对以图表方式来表达数学上的关联很有兴趣”。简单的说：就是类似于数学用表一样，通过查找，知道反射系数的数值。

对史密斯圆图的理解

传输线的阻抗由于电容电感等的影响，是一个复阻抗，所以我们将其放在这个复数坐标系中，就是下图：

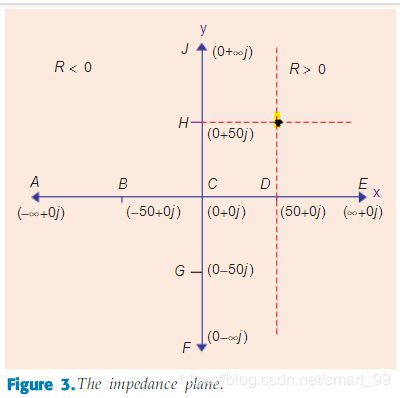
比如，此时传输线阻抗为两条红曲线的交点，那么变换到天才的史密斯圆图上就是下图这里：
值得说明的是，下图中的X、Y轴不再直接代表着阻抗了。

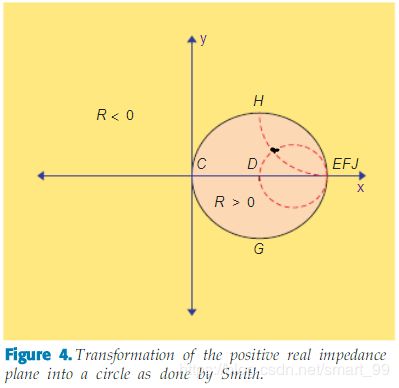
此时大家一定很好奇，怎么从复数坐标系变换到史密斯圆图的。且看下面的过程：

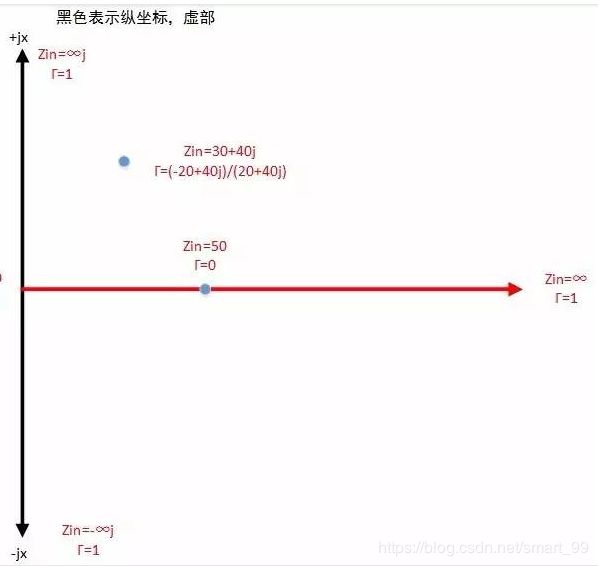
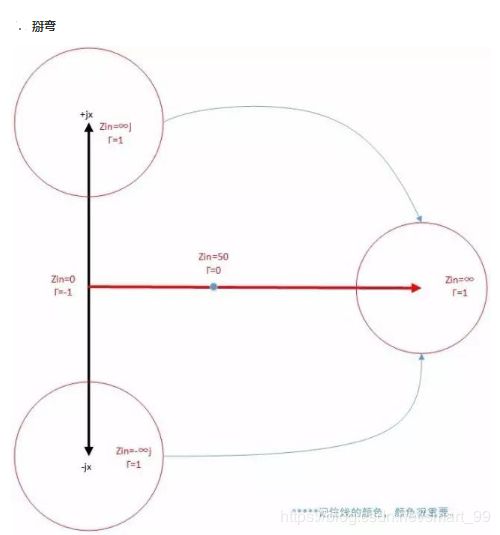
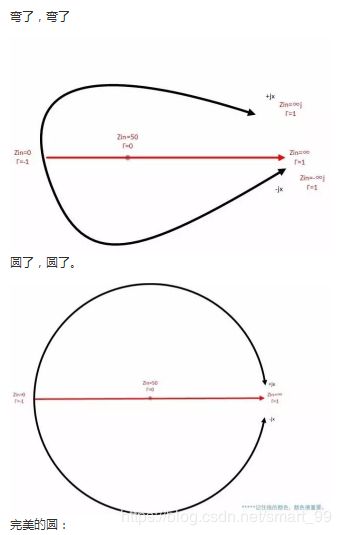
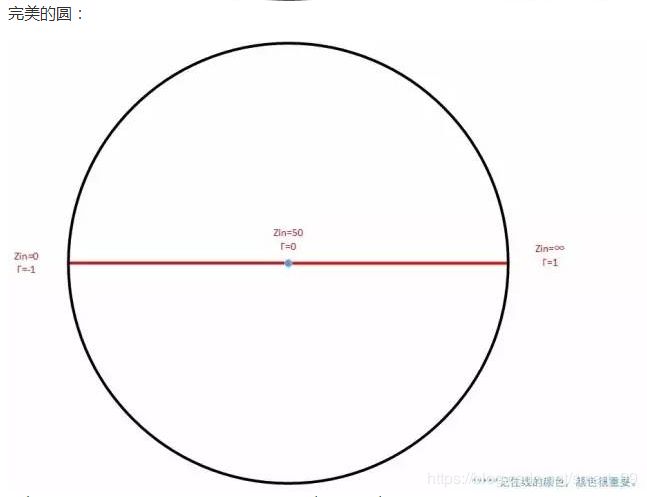
这里最后得到的圆，进行归一化处理之后，就是史密斯圆图。对于其中的各项运用技巧，如反射系数的计算以及阻抗圆图和导纳圆图的运用等，因为资料太多，本文就不再赘述了。

顺便说一个容易混淆的地方：通常看到的圆图是阻抗圆图，有时要用到导纳圆图，两者有异曲同工之妙，呈对称态，而不变的则是圆图右边都是开路点，左边都是短路点。

好的，接下来，
我们看到圆图是在向正半轴方向变换，而负半轴方向在圆图中无法体现。
那负半轴怎么表现出来呢？
就需要我们的三维圆图了。

最新发展情况：三维球体史密斯圆图

1.拓展原因

上图是史密斯圆图在坐标系中位置，我们可以看到它只能表示正阻抗的情况。
在涉及到负电阻时，用一个三维球面而不是二维圆周的方式来表示史密斯圆图时，可以更好地洞察匹配问题的实质。将要讨论一种把阻抗域的负实数部半边结合进入扩展的史密斯圆图的有效方法。

2.拓展方法

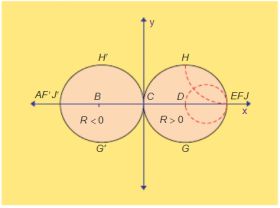
要考虑到负阻抗的情况，我们就需要再引入第二个圆图，它们背对背拥抱（滥用沉默在咆哮。。。）。但这样两个圆图不方便工程中的应用，而且容易混淆，所以我们就可以将这两个二维的圆图，翻转拼接成为一个三维球体圆图，如下图：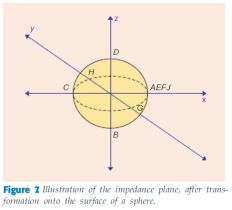
当然这的确是一个球体史密斯圆图，但我觉得叫伪三维圆图更恰当，因为只有球体表面有意义，球体内部是没有什么意义的，可以不用考虑。

3.拓展形式

在这个新形式的史密斯圆图中，阻抗为0 和无穷时的点在x 轴上。从Z 轴的正方向去看球体，可以看到一个类似于传统的史密斯圆图。当然，由于球面的曲线特性，这个圆周的形状似乎有些变形。当把阻抗平面映射到球面上时，整个平面都在一个易于处理的区域内，而且正电阻到负电阻的过渡可以平滑连续地进行。

Z>0 的半球表面含有所有具有正电阻的阻抗，Z<0含有所有具有负电阻的阻抗。类似地，y>0 的半球含有感抗阻抗，y<0 的半球含有容抗阻抗。只有在球面上的点才有意义；在球体内的点则无关紧要。
现在球形的史密斯圆图已经建成了，正如2-D 史密斯圆图一样，我们可以考虑不同阻抗的表示方式。
首先，电阻为常数和感抗为常数的线可以先画出来。这些线形成了一系列封闭的圆周，起始和中止于点（1，0，0）。例如，+50，+50j，-50，-50j 这些常数电阻和感抗线都从点AEFJ（北极）开始，再回到起点前，跨经点D，H，B 和G（在赤道上）。画出其它值的电阻和电抗线使其类似于2-D 史密斯圆图。
不仅如此，还可以画出品质因数。

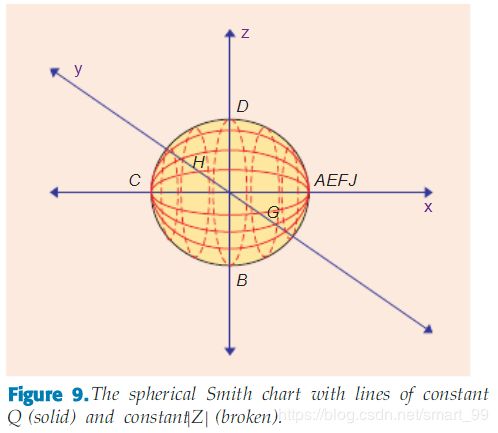
这会形成阻抗从零到无穷大的一系列弧线。当Q=0 时（理想的电阻），弧线便成为一条从零到无穷大的直线，当Q 为无穷大时（一个理想的电感或电容），弧线是沿着史密斯图的圆周线的。在球形的史密斯圆图上，Q 为常数的线便形成了从北极Z=无穷大到南极Z=0 的弧线。见图9。在x-y 平面上的Q 等值的圆周上具有一个零值，同时在x-y 平面上的具有一个Q 为无穷大的Q 等值圆周。使用球形史密斯圆图，当电阻为负的时候，也可以很容易地使用Q 线。图9 中增加了纬线。这些纬线是由|Z|为常数时所形成的。赤道线代表的是|Z|=50Ω。

发展基础：

史密斯圆图的基本在于以下的算式

Γ代表其线路的反射系数(reflection coefficient)，即S-parameter里的S11，Z是归一负载值，即ZL / Z0。当中，ZL是线路的负载值
Z0是传输线的特征阻抗值，通常会使用50Ω。
而史密斯圆图则把“零”和“无穷大”都拉到了图内。

圆图中的横坐标代表反射系数的实部，纵坐标代表虚部。圆形线代表等电阻圆，每个圆的圆心为1/(R+1),半径为R/(R+1).R为该圆上的点的电阻值。
中间的横线与向上和向下散出的线则代表阻抗的虚数值，即等电抗圆，圆心为1/X,半径为1/X.由于反射系数是小于等于1的，所以在等电抗圆落在单位圆以外的部分没有意义。当中向上发散的是正数，向下发散的是负数。
圆图最中间的点(Z=1+j0, Γ=0)代表一个已匹配(matched)的电阻数值(此ZL=Z0，即Z＝1)，同时其反射系数的值会是零。圆图的边缘代表其反射系数的幅度是1，即100%反射。

有一些圆图是以导纳值(admittance)来表示，把上述的阻抗值版本旋转180度即可。

圆图中的每一点代表在该点阻抗下的反射系数。该电的阻抗实部可以从该电所在的等电阻圆读出，虚部可以从该点所在的等电抗圆读出。同时，该点到原点的距离为反射系数的绝对值，到原点的角度为反射系数的相位。
由反射系数可以得到电压驻波比和回波损耗。
VSWR=(1+|Γ|)/(1-|Γ|).
Ploss＝10lg|Γ|2=20lg|Γ|
关于阻抗匹配的应用：
把阻抗圆图与导纳圆图合并使用，可以把任意阻抗点通过沿等电阻圆，等电抗圆，等电纳圆和等电导圆移动而匹配到原点（即阻抗匹配点）上。不同的移动方式对应不同的元件连接。

或许受到黎曼几何的启发，将直角坐标系中的直线变化成为曲线，

应用：

阻抗匹配

阻抗匹配（Impedancematching）是微波电子学里的一部分，负载阻抗与激励源内部阻抗互相适配，得到最大功率输出的一种工作状态,主要用于传输线上，来达至所有高频的微波信号皆能传至负载点的目的，不会有信号反射回来源点，从而提升能源效益。对于不同特性的电路，匹配条件是不一样的。在纯电阻电路中，当负载电阻等于激励源内阻时，则输出功率为最大，这种工作状态称为匹配，否则称为失配。当激励源内阻抗和负载阻抗含有电抗成份时，为使负载得到最大功率，负载阻抗与内阻必须满足共轭关系，即电阻成份相等，电抗成份只数值相等而符号相反。这种匹配条件称为共轭匹配。

匹配条件

①负载阻抗等于信源内阻抗，即它们的模与辐角分别相等，这时在负载阻抗上可以得到无失真的电压传输。
②负载阻抗等于信源内阻抗的共轭值，即它们的模相等而辐角之和为零。这时在负载阻抗上可以得到最大功率。这种匹配条件称为共轭匹配。如果信源内阻抗和负载阻抗均为纯阻性，则两种匹配条件是等同的。

结论

重点讨论了传统2-D 史密斯圆图的局限性。提出了一种克服这些局限的扩展史密斯圆图的想法。这种扩展包括从2-D 阻抗平面转换到三维，并将其映射到球体的表面。