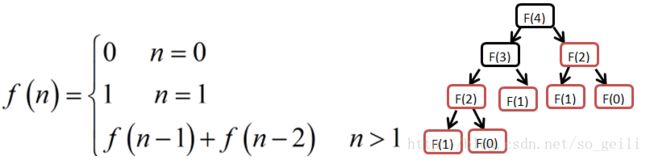算法导论-----动态规划是什么
目录
- 一、动态规划概述
- 二、动态规划三要素
- 三、动态规划和静态规划的关系
- 四、仅有动态规划是不够的—–贪婪策略的出现
- 五、参考资料
《算法导论》中并没有把动态规划的来龙去脉介绍清楚,网上很多讲解都是动态规划的数学模型,感觉没必要系统的学习动态规划的数学定义,把人搞晕了。本文更像是一篇科普,方便理解什么是动态规划。
一、动态规划概述
动态规划(Dynamic Programming)通常是用来解决最优化问题的。最初是由数学家在研究多阶段决策过程的优化问题时,提出的优化原理,把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决优化问题的方法。值得注意的是动态规划的英文名dynamic programming ,这个名字看上去似乎和程序设计有关,然而这么理解就错了。这里的programming和程序设计没有任何关系,而是指表格查询法(tabular method),即将每一步计算的结果存储在表格里,供随后的计算使用。[举例说明的话太长,大致理解一下即可]
一般的组合优化问题都有对应的 目标函数和 约束条件。组合优化问题的 解分布在搜索空间中,其中满足约束条件的解称为 可行解,而在可行解中使得目标函数达到最小(或最大)的解称为 最优解(the optional solution),最优解可能存在多个。所谓求解组合优化问题就是找到该问题的最优解。
如今动态规划技术已经被广泛应用于许多组合优化问题的算法设计中,如图的 多起点与多终点的最短路径问题、矩阵链的乘法问题、最大效益投资问题、背包问题、最长公共子序列问题、图像压缩问题、最大子段和问题、最优二分检索树问题、RNA的最优二级结构问题等。
需要注意的是:在口语交流时,大家常常说“动态规划算法”,但动态规划是求解最优化问题的一种途径、一种方法,而不是一种特定的算法。
在学习《算法导论》书中的动态规划之前,一般都学习过分治法。
分治法中的各个子问题是独立的(不包含公共的子问题),因此只要递归地求出各个子问题的解后,便可自下而上地将子问题的解合并成原问题的解。
partition the problem into disjoint(不相交) subproblems, solve the subproblems recursively, and then combine their solutions to solve the original problem.————《divide-and-conquer》
但分治后, 如果各个子问题是不独立的,则分治法要做很多不必要的工作(即重复地解公共的子问题),对时间的消耗很大。例如在Fibonacci数列中递归的求解 F(4) ,重复计算子问题 F(2) ,影响求解效率(如下图所示)。在求解 F(n) 时,不仅时间复杂度是指数级的,而且反复递归调用时可能导致栈溢出。
在上面的例子中,由于经分解得到的各个子问题不独立,就适合用动态规划求解问题。在求解的过程中,将已解决的子问题的解保存起来,在需要的时候可以轻松找出。通常采用表(table)的形式保存中间子问题的结果。这样就可以避免大量无意义的重复计算,从而降低算法的时间复杂度。在此要强调的是:解决问题、提高效率是动态规划的任务,但却不是动态规划的全部。因为我们不只是要解决一个问题,而是要以最优的方式解决这个问题。
小结:动态规划的实质就是分治思想和解决冗余。将原来具有指数级复杂性的算法改进成具有多项式时间的算法,这是动态规划算法的目的。由于在实现的过程中,需要存储各种状态,所以它的空间复杂性要大于其他算法,这是一种以空间换取时间的技术。
二、动态规划三要素
所有的算法都有局限性,超出特定条件,它就失去了作用。同样采用该算法要满足三个基本要素:最优子结构性质、子问题重叠性、自底向上的求解方法。在这三个要素的指导下,可以对某问题是否适合采用动态规划算法进行求解进行预判。
1.最优子结构性质 (optimal sub-structure)
最优子结构性质,通俗的说法就是问题的最优解包含其子问题的最优解。任何问题,如果不具备该性质,就不能用动态规划来解决。常用反证法分析论证问题是否具备最优子结构性质。
有时对某个子问题的解不一定达到最优,但是当把它延伸成整个问题的解时反而成了最优解,这种问题不满足最优子结构性质,无法使用动态规划。
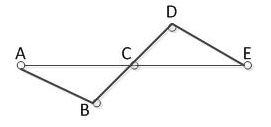
最优子结构性质见上面的示意图:如果节点A到节点E的最长路径是 (A−>B−>C−>D−>E) ;那么,节点C到节点E的最长路径必定在此路径( A−>B−>C−>D−>E )上!
在知道什么是最优子结构性质后,怎么利用这个性质设计动态规划算法呢?首先,要明确动态规划是基于分治策略的,会将原问题分解为一个或多个子问题。我们要根据具体问题,考虑所有选择所产生的子问题,然后从中选择一个最优的选项。比如在最长公共子序列LCS问题中,选择是根据 xi=yj 成立与否分为1个或2个选项。
- 如果 xm=yn ,则 zk=xm=yn 且 Zk−1 是 Xm−1 和 Yn−1 的一个LCS。
- 如果 xm≠yn ,那么 zk≠xm ,意味着 Z 是 Xm−1 和 Y 的一个LCS。
- 如果 xm≠yn ,那么 zk≠yn ,意味着 Z 是 X 和 Yn−1 的一个LCS。
从上述的结论可以看出,两个序列的LCS问题包含两个序列的前缀的LCS,因此,LCS问题具有最优子结构性质。为设计递归算法,我们可以进一步利用最优子结构性质写出问题的递归方程。设 C[i,j] 表示 Xi 和 Yj 的最长公共子序列LCS的长度。如果 i=0 或 j=0 ,即一个序列长度为 0 时,那么LCS的长度为0。根据LCS问题的最优子结构性质,可得如下公式:
从而编写基于动态规划的递归算法。
2.子问题重叠性质 (subproblems overlap)
Dynamic programming solves each subsubproblem just once and then saves its answer in a table, thereby avoiding the work of recomputing.
子问题重叠性质并不是动态规划适用的必要条件,但是如果该性质无法满足,动态规划算法同其他算法相比就不具备优势。
3.自底向上的求解方法 (bottom-up method)
由于动态规划解决的问题具有子问题重叠性质,求解时需要自底向上的方法,即:首先选择合适的表格(一维或二维),将递归的停止条件填入表格的相应位置;然后将问题的规模一级一级放大,求出每一级子问题的最优质,并将其填入表格的相应位置,直到问题所要求的规模,此时求出的便是原问题的最优值。
除了自底向上法之外,还可以使用“ 带备忘录的自顶向下法”(top-down with memoization)。此方法仍按自然的递归形式编写过程,但过程会保存每个子问题的解(用数组或散列表保存)。当需要子问题的解时,过程首先检查是否已经保存过此解。如果是,直接返回保存的值,从而节约计算时间;否则,按通常方式计算这个子问题。这个递归过程是带备忘的,因为它“记住了”之前已经计算出的结果。
三、动态规划和静态规划的关系
算法世界中确实还存在静态规划的概念,只不过不是被直接称呼为静态规划,而是有着更加动听的名字:线性规划和非线性规划。
与静态规划相比,动态规划具有许多优越性:
- 动态规划的核心是找到一个问题所包含的子问题及其表现形式。找子问题的表现形式需要创造力和实验,但也存在着一些常用的形式,如:子问题是原问题的前缀、中缀,子问题是原问题的子树。因此,动态规划常有迹可循。
- 动态规划比静态规划更容易得到最优解。静态规划可能由于约束条件确定的约束集合复杂而变得困难。而动态规划把原问题分解为一系列结构相似的子问题,每个子问题的变量个数大大减小,约束集合也简单地多,因此更易求解。
- 动态规划可以得到一族最优解(原问题和子问题的最优解),而非线性规划只能得到全过程的最优解。
- 动态规划的时间效率可以容易获得:子问题数量×子问题的时间效率。
与静态规划相比,动态规划也存在缺点:
- 找出子问题的表现方式需要创造力和实验,经常需要对每类问题进行具体分析,非熟练的分析人员难以准确对原问题进行合理分解,导致应用上的局限。
- 状态空间可能呈指数增长。如果一维状态变量有m个取值,则n维问题的状态就有 mn 个值。对于n较大的实际问题,其计算成本上无法容忍。
静态规划和动态规划是可以相互转化的。原理复杂,能力有限,不做介绍。
四、仅有动态规划是不够的—–贪婪策略的出现
动态规划的一个关键特点是每次做选择之前,对所有选择的效果进行计算。在计算的结果上选择能够达到最优的选项,从而保证每次选择都是最优的。但是,这种策略在当选项的数量非常巨大的时候将不堪重负。例如在下围棋的时候,如果采用动态规划策略,则需要先对每步可能的行棋的影响进行计算,然后比较选择最优的走法。但每一步可进行的走法实在太多,如果再考虑到一盘棋有几乎不计其数的步骤,所以计算任务非常大几乎不可能完成。这种情况就是上面介绍的动态规划缺点。这个时候应该采用新的策略———贪婪策略。
贪婪策略允许我们不对所有可能选择的影响计算一遍后做出决策。我们可以在进行选择的时候不进行任何计算,而根据当时的情况作出我们认为最好的选择,这样我们就避免了大量计算,从而大大提高算法的效率。贪婪策略后面进行详细的总结。
五、参考资料
- 《算法导论》 原书第三版 殷建平等译
- 《算法之道》 机械工业出版社 邹恒明著
- 《算法设计与分析》 清华大学出版社 王秋芬等编著
- 《算法设计与分析》 清华大学出版社 屈婉玲等编著