谱聚类（Spectral Clustering）原理及Python实现

谱聚类原理及Python实现

图模型

  无向带权图模型 G=<V,E> G =< V , E > ，每一条边上的权重 wij w i j 为两个顶点的相似度，从而可以定义相似度矩阵 W W ，此外还可以定义度矩阵 D D 和邻接矩阵 A A ，从而有拉普拉斯矩阵 L=D−A L = D − A 。所以本文用到的矩阵总共两个： L L 和 W W 。

图的分割

  一个图 G G 可能有很多个子图 Gi G i （总共 k k 个），现在的任务是将大图分成若干小块，要求分法是最佳的。何为“最佳”呢，遍历每一个子图，计算一个切图惩罚，将他们加起来。式中的 Ĝ i G ^ i 表示子图 Gi G i 的补集，代价函数 C C 计算的是连接两个子图之间的权重之和。

Cost(G1,⋯,Gk)=∑iC(Gi,Ĝ i)C(G1,G2)=∑i∈G1,j∈G2wij C o s t ( G 1 , ⋯ , G k ) = ∑ i C ( G i , G ^ i ) C ( G 1 , G 2 ) = ∑ i ∈ G 1 , j ∈ G 2 w i j

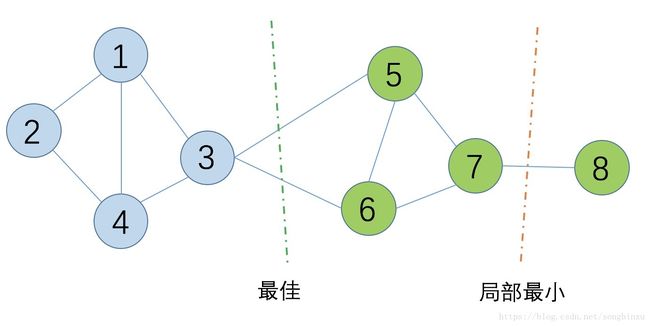
  根据这个公式，对于下面这个图，假设点7和点8之间的权重值很小，那么很容易有红线所示的划分（假设二分），上面的代价函数计算出来的值很小。但显然绿色线所示才是最佳的分法。

距离度量与邻接矩阵

  邻接矩阵某种程度上反映了图中各结点之间的相似性，普通的邻接矩阵元素非0即1，谱聚类中的邻接矩阵用KNN来计算。具体来说，遍历每一个结点 xi x i ，根据相似度（或距离）矩阵找出它的 k k 个最接近的点，构成 xi x i 的邻域 Ni N i ，然后按以下规则之一构造邻接矩阵。

Aij=Aji={0exp−||xi−xj||22σ2xi∉Nj andxj∉ Nixi∈Nj or xj∈Ni A i j = A j i = { 0 x i ∉ N j   a n d x j ∉   N i exp − | | x i − x j | | 2 2 σ 2 x i ∈ N j   o r   x j ∈ N i

Aij=Aji={0exp−||xi−xj||22σ2xi∉Nj or xj∉ Nixi∈Nj and xj∈Ni A i j = A j i = { 0 x i ∉ N j   o r   x j ∉   N i exp − | | x i − x j | | 2 2 σ 2 x i ∈ N j   a n d   x j ∈ N i

切图聚类

RatioCut 切法

  为了解决上面这个局部最优问题，一个很自然的做法就是改进目标函数，要求每个划分出来的子图的结点数尽量大。例如上图，最佳划分对应的两个子图节点数都是4，而局部最优划分有一个子图节点数为1。

RatioCut(G1,⋯,Gk)=∑iC(Gi,Ĝ i)|Ĝ i| R a t i o C u t ( G 1 , ⋯ , G k ) = ∑ i C ( G i , G ^ i ) | G ^ i |

  为了求解 minRatioCut(G1,⋯,Gk) min R a t i o C u t ( G 1 , ⋯ , G k ) ，引入指示向量 f=(f1,f2,⋯,fk) f = ( f 1 , f 2 , ⋯ , f k ) ，每一个 fj f j 对应于一个子图 Gj G j ，是一个 n n 维向量，每一维对应图中一个结点。意思就是每个子图 Gj G j 维护一个 n n 维向量，将自己的点指示为常数，其余为0。

hji={1|Gj|√0vi∈Gjvi∉Gj h j i = { 1 | G j | v i ∈ G j 0 v i ∉ G j

  这样构造矩阵 Hk×n H k × n 有个特点，由于子图之间互斥，故 H H 每一列只能有一个1，于是 hj h j 之间都是正交的（即任意两行正交），因此矩阵相乘有 HTH=I H T H = I

  由拉普拉斯矩阵的性质可知，两个子图的情况：

hTjLhj=12∑m∑nwmn(hjm−hjn)2=12⎛⎝⎜⎜∑m∈Gj∑n∉Gjwmn(1|Gj|‾‾‾‾√−0)2+∑m∉Gj∑n∈Gjwmn(0−1|Gj|‾‾‾‾√)2⎞⎠⎟⎟=12⎛⎝⎜⎜∑m∈Gj∑n∉Gjwmn|Gj|+∑m∉Gj∑n∈Gjwmn|Gj|⎞⎠⎟⎟=Cost(Gj,Ĝ j)|Gj|=RatioCut(Gj,Ĝ j) h j T L h j = 1 2 ∑ m ∑ n w m n ( h j m − h j n ) 2 = 1 2 ( ∑ m ∈ G j ∑ n ∉ G j w m n ( 1 | G j | − 0 ) 2 + ∑ m ∉ G j ∑ n ∈ G j w m n ( 0 − 1 | G j | ) 2 ) = 1 2 ( ∑ m ∈ G j ∑ n ∉ G j w m n | G j | + ∑ m ∉ G j ∑ n ∈ G j w m n | G j | ) = C o s t ( G j , G ^ j ) | G j | = R a t i o C u t ( G j , G ^ j )

好像很长，总结起来就是： RatioCut(Gj,Ĝ j)=hTjLhj R a t i o C u t ( G j , G ^ j ) = h j T L h j

推广到 k k 个子图，于是乎求解 RatioCut R a t i o C u t 等价于求矩阵 HTLH H T L H 的迹：

RatioCut(G1,G2,⋯,Gk)=∑jhTjLhj=∑j(HTLH)jj=tr(HTLH) R a t i o C u t ( G 1 , G 2 , ⋯ , G k ) = ∑ j h j T L h j = ∑ j ( H T L H ) j j = t r ( H T L H )

  对于任意一个给定的图，它的拉普拉斯矩阵 L L 是固定的，因此优化目标变成求解使得RatioCut最小的 H H ，每一个特定的 Hn×k H n × k 对应着对图的一种划分方法（ k k 分），找到这个 H H ，就等于找到了最佳的划分（聚类）。

s.t.argminHtr(HTLH)HTH=I arg ⁡ min H t r ( H T L H ) s . t . H T H = I

  留意矩阵 HTLH H T L H 是一个 k×k k × k 对角阵，各元素是 hTjLhj h j T L h j ，想要 tr t r 最小，即个对角线元素加起来最小，即要求每个优化字母表 hTjLhj h j T L h j 都尽量小。那么要怎么求 hTjLhj h j T L h j 呢？答案是：将问题转化为计算拉普拉斯矩阵 L L 的 k k 个最小的特征值。
  现在我们先做一个归一化，使得任意 hj h j 满足 hTjhj=1 h j T h j = 1

hji←hji(∑kt=1h2jt)1/2 h j i ← h j i ( ∑ t = 1 k h j t 2 ) 1 / 2

  有了这个条件我们就可以利用瑞利熵的性质来求 L L 的特征值：

R(L,hj)=hTjLhjhTjhj=hTjLhj=λ R ( L , h j ) = h j T L h j h j T h j = h j T L h j = λ

  求得 k k 个最小的特征值，对应的 k k 个 n n 维特征向量拼起来就是我们所需要的 H H 矩阵。然而，仅取 k k 个特征值的做法会损失信息，因此现在得到的 H H 还不能直接用来指示每个结点属于哪个子图。
  一般还需要对 Hn×k H n × k 做一次 Kmeans 聚类。具体来说，将 Hn×k H n × k 的每一行（ k k 维向量）当做一个样本的特征向量，然后用Kmeans聚类（设聚类个数是 K K ，并没有要求 K=k K = k ），将样本聚成 C=(c1,c2,⋯,cK) C = ( c 1 , c 2 , ⋯ , c K ) 。

NCut 切法

  RatioCut目标函数的分母是子图的点个数，NCut类似，分母换成子图中边的权重之和。

NCut(G1,⋯,Gk)=∑iC(Gi,Ĝ i)vol(Ĝ i)vol(G=<V,E>)=∑vi∈V∑vj∈Vwij N C u t ( G 1 , ⋯ , G k ) = ∑ i C ( G i , G ^ i ) v o l ( G ^ i ) v o l ( G =< V , E > ) = ∑ v i ∈ V ∑ v j ∈ V w i j

定义指示变量：

hji=⎧⎩⎨⎪⎪1vol(Ĝ j)√0vi∈Gjvi∉Gj h j i = { 1 v o l ( G ^ j ) v i ∈ G j 0 v i ∉ G j

它的特点是 HTDH=I H T D H = I

hTjDhj=∑jh2ijdj=1vol(Gj)∑vi∈Gjwi=vol(Gj)vol(Gj)=1 h j T D h j = ∑ j h i j 2 d j = 1 v o l ( G j ) ∑ v i ∈ G j w i = v o l ( G j ) v o l ( G j ) = 1

同RatioCut，可以推出：

NCut(Gj,Ĝ j)=hTjLhjNCut(G1,G2,⋯,Gk)=∑jhTjLhj=∑j(HTLH)jj=tr(HTLH) N C u t ( G j , G ^ j ) = h j T L h j N C u t ( G 1 , G 2 , ⋯ , G k ) = ∑ j h j T L h j = ∑ j ( H T L H ) j j = t r ( H T L H )

优化目标：

s.t.argminHtr(HTLH)HTDH=I arg ⁡ min H t r ( H T L H ) s . t . H T D H = I

令 H=D−1/2F H = D − 1 / 2 F ， HTLH=FTD−1/2LD−1/2F H T L H = F T D − 1 / 2 L D − 1 / 2 F ， HTDH=FTF=I H T D H = F T F = I ，即：

s.t.argminFtr(FTD−1/2LD−1/2F)FTF=I arg ⁡ min F t r ( F T D − 1 / 2 L D − 1 / 2 F ) s . t . F T F = I

所以问题变成了求矩阵 D−1/2LD−1/2 D − 1 / 2 L D − 1 / 2 的 k k 个最小的特征值。

---

Python实现

谱聚类整体流程

1. 计算距离矩阵（例如欧氏距离）
2. 利用KNN计算邻接矩阵 A A
3. 由 A A 计算度矩阵 D D 和拉普拉斯矩阵 L L
4. 标准化 L→D−1/2LD−1/2 L → D − 1 / 2 L D − 1 / 2
5. 对矩阵 D−1/2LD−1/2 D − 1 / 2 L D − 1 / 2 进行特征值分解，得到特征向量 Hnn H n n
6. 将 Hnn H n n 当成样本送入 Kmeans 聚类
7. 获得聚类结果 C=(C1,C2,⋯,Ck) C = ( C 1 , C 2 , ⋯ , C k )

1. 距离矩阵

def euclidDistance(x1, x2, sqrt_flag=False):
    res = np.sum((x1-x2)**2)
    if sqrt_flag:
        res = np.sqrt(res)
    return res

def calEuclidDistanceMatrix(X):
    X = np.array(X)
    S = np.zeros((len(X), len(X)))
    for i in range(len(X)):
        for j in range(i+1, len(X)):
            S[i][j] = 1.0 * euclidDistance(X[i], X[j])
            S[j][i] = S[i][j]
    return S

2. 邻接矩阵

def myKNN(S, k, sigma=1.0):
    N = len(S)
    A = np.zeros((N,N))

    for i in range(N):
        dist_with_index = zip(S[i], range(N))
        dist_with_index = sorted(dist_with_index, key=lambda x:x[0])
        neighbours_id = [dist_with_index[m][1] for m in range(k+1)] # xi's k nearest neighbours

        for j in neighbours_id: # xj is xi's neighbour
            A[i][j] = np.exp(-S[i][j]/2/sigma/sigma)
            A[j][i] = A[i][j] # mutually

    return A

3. 标准化的拉普拉斯矩阵

def calLaplacianMatrix(adjacentMatrix):

    # compute the Degree Matrix: D=sum(A)
    degreeMatrix = np.sum(adjacentMatrix, axis=1)

    # compute the Laplacian Matrix: L=D-A
    laplacianMatrix = np.diag(degreeMatrix) - adjacentMatrix

    # normailze
    # D^(-1/2) L D^(-1/2)
    sqrtDegreeMatrix = np.diag(1.0 / (degreeMatrix ** (0.5)))
    return np.dot(np.dot(sqrtDegreeMatrix, laplacianMatrix), sqrtDegreeMatrix)

4. 特征值分解

lam, H = np.linalg.eig(Laplacian) # H'shape is n*n

5. Kmeans

from sklearn.cluster import KMeans
def spKmeans(H):
    sp_kmeans = KMeans(n_clusters=2).fit(H)
    return sp_kmeans.labels_

github

https://github.com/SongDark/SpectralClustering

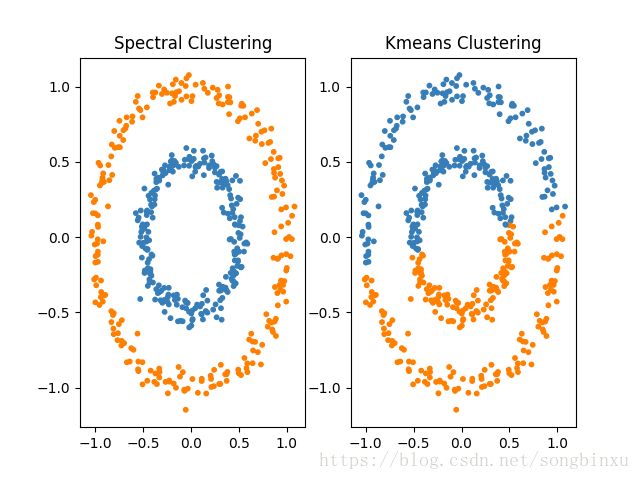
  聚类结果如下，左边是谱聚类，右边是Kmeans聚类，显然谱聚类效果更好。其实sklearn已经有实现谱聚类（sklearn.cluster.SpectralClustering），嫌麻烦的可以直接调用，我只是为了搞懂谱聚类算法的一些细节才参照着其他文章自己用python重新实现了一遍。

---

总结

  谱聚类是一种基于数据相似度矩阵的聚类方法，它定义了子图划分的优化目标函数，并作出改进（RatioCut和NCut），引入指示变量，将划分问题转化为求解最优的指示变量矩阵 H H 。然后利用瑞利熵的性质，将该问题进一步转化为求解拉普拉斯矩阵的 k k 个最小特征值，最后将 H H 作为样本的某种表达，使用传统的聚类方法进行聚类。
  我对于谱聚类的理解是，原本相似度矩阵就是对样本点的一种特征表达（特征维数等于样本数），现在进行了谱聚类求得的特征值矩阵，实际上是对原始特征矩阵的一种降维（也可能是升维），总之就是将样本从原始空间变换（可能是线性的也可能是非线性的）到另一个空间，在这个空间中具有良好的全局欧式性。

---

参考资料

【博客】谱聚类（spectral clustering）原理总结
【博客】谱聚类（spectral clustering)及其实现详解
【博客】谱聚类算法(Spectral Clustering)
【Codes】pspectralclustering
【Paper】Parallel Spectral Clustering in Distributed Systems
【API】sklearn.cluster.SpectralClustering
【Demo】Comparing different clustering algorithms on toy datasets