NLP-隐马尔可夫模型及使用实例

• 说明：学习笔记，内容来自周志华的‘机器学习’书籍和加号的‘七月在线’视频。

隐马尔可夫模型

隐马尔可夫模型（Hidden Markov Model，简称HMM）是结构最简单的动态贝叶斯网，这是一种著名的有向图模型，主要用于时序数据建模，在语音识别、自然语言处理等领域有广泛应用。——周志华《机器学习》

1.隐马尔可夫模型的结构信息：

隐马尔可夫模型中的变量可以分为两组，第一组是状态变量{ y1,y2,...,yn y 1 , y 2 , . . . , y n },，其中 yi∈y y i ∈ y 表示第 i i 时刻的系统状态，通常假定状态变量是隐藏的、不可被观测的，因此状态变量也被称为隐变量。第二组是观测变量{ x1,x2,..,xn x 1 , x 2 , . . , x n },其中 xi∈x x i ∈ x 表示第 i i 时刻的观测值，如下图所示：

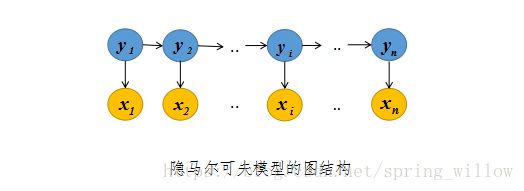
模型的图结构看起来有点类似于我们熟知的RNN模型。图中的箭头表示变量之间的依赖关系。在任意时刻，观测变量的取值仅依赖于状态变量，与其他状态变量和观测变量的取值无关。同时， t t 时刻的状态仅依赖于 t−1 t − 1 时刻的状态，与其余状态无关，这就是所谓的马尔可夫链。
基于上述的依赖关系，我们得到所有变量的联合概率分布为：

P(x1,y1,...,xn,yn)=P(y1)P(x1|y1)∏i=2nP(yi|yi−1)P(xi|yi) P ( x 1 , y 1 , . . . , x n , y n ) = P ( y 1 ) P ( x 1 | y 1 ) ∏ i = 2 n P ( y i | y i − 1 ) P ( x i | y i )

2.确定一个隐马尔可夫模型需要以下三组参数：

• 状态转移概率：
  模型在各个状态间转换的概率，可以用矩阵 A A 表示
• 输出观测概率：
  模型根据当前状态获得各个观测值的概率，可以用矩阵 B=[bij]N∗M B = [ b i j ] N ∗ M 表示， N N 大小为隐藏状态数， M M 大小为观测值数
• 初始状态概率：
  模型在初始时刻各状态出现的概率，通常记为 π=(π1,π2,..,πn) π = ( π 1 , π 2 , . . , π n )

通过 λ=[A,B,π] λ = [ A , B , π ] 就可以指代一个隐马尔可夫模型。
我们使用一个用烂了的例子来对这几种参数进行说明，如下图所示：

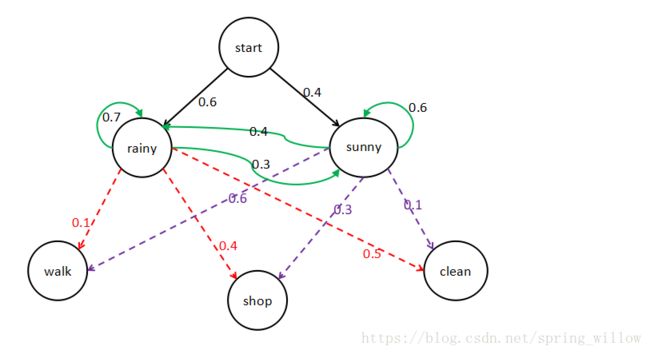
说明：
①图中start表示初始状态，则 π=(0.6,0.4) π = ( 0.6 , 0.4 ) ；
②rainy表示下雨天，sunny表示晴天，当第一天是下雨天的时候，第二天仍然是下雨天的概率是0.7，晴天的概率是0.3；当第一天是晴天时候，第二天是下雨天的概率是0.4，仍然是晴天的概率是0.6；这里的晴天和雨天就是我们模型中所说的隐藏状态。
状态转换概率矩阵 A A ：

A=[0.70.40.30.6] A = [ 0.7 0.3 0.4 0.6 ]

③walk、shop、clean表示在下雨天或者晴天的时候我们散步、逛街和打扫房间的可能情况，也就是模型中所说的观测变量，在下雨天打扫房间的概率是0.5；晴天的时候更可能出去逛街，所以概率是0.6，通过该图我们可以得到输出观测概率矩阵 B B ：

B=[0.10.60.40.30.50.1] B = [ 0.1 0.4 0.5 0.6 0.3 0.1 ]

3.实际应用中人们常关注的HMM模型的三个基本问题：

• 评估模型与观测序列之间的匹配程度：
  给定模型 λ λ ，如何计算其产生观测序列{ x1,x2,..,xn x 1 , x 2 , . . , x n }的概率 P(x|λ) P ( x | λ ) ？
• 根据观测序列推断隐藏的模型状态：
  给定模型 λ λ 以及观测序列{ x1,x2,..,xn x 1 , x 2 , . . , x n }，如何找到与此观测序列最匹配的状态序列{ y1,y2,...,yn y 1 , y 2 , . . . , y n }？
• 训练模型使其更好的描述观测序列：
  给定观测序列{ x1,x2,..,xn x 1 , x 2 , . . , x n }，如何调整参数 λ λ ，使得该序列出现的概率 P(x|λ) P ( x | λ ) 最大？

针对上面的是哪个问题，分别有下面几种解决方法：

• 问题1：遍历算法、前向算法、后向算法
• 问题2：Viterbi 维特比算法
• 问题3：Baum-Welch 鲍姆-韦尔奇算法