【图机器学习】cs224w Lecture 8 & 9 - 图神经网络 及 深度生成模型

转自本人：https://blog.csdn.net/New2World/article/details/106160122

Graph Neural Network

这一课主要讲了如何用深度学习的方法来做 embedding，也就是最近很火的 Graph Neural Network 图神经网络。之所以想到要用 GNN 是因为之前提到的 embedding encoder 其实是一种 shallow encoder，即类似与所有节点的 embedding 是一个矩阵，每个节点对应一列。在使用的时候就是一个简单的 look up 的过程，而这样做的缺陷在于

1. 没有共享参数，总参数量为 \(O(|V|)\)
2. 不能泛化到没见过的节点上
3. 只考虑了网络结构信息而没有综合节点特征

Graph Convolutional Network

现在比较成熟的卷积神经网络其实可以看作一种特殊的图网络，因为图片类似于 \(4\)-regular 的图，而图片中的像素就像一个个节点。图片上的卷积操作其实就是位于卷积核中心的像素(节点)从相邻像素(节点)获取信息的过程。

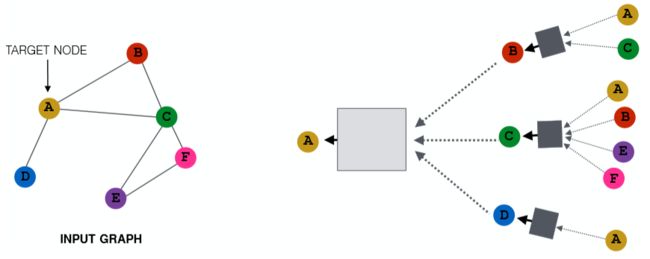
那么把卷积神经网络的思想迁移过来，对于每个图中的节点，我们聚合它周围的节点信息就能实现类似卷积的操作。如上图，对于节点 A 我们将它的邻接点聚合起来。而对于 A 的邻接点也采取同样的操作，那么我们就能得到一棵树。可以将这棵树看作节点 A 独一无二的一张计算图，从中我们可以得到包含了 local network neighborhoods 信息的 embedding。这里这个聚合的范围，可以看作 A 捕获了多大区域内的 local 信息，或者说我们延伸了多少个 hops。从 Lecture 2 中的随机图可知，路径平均长度为 \(6\)，因此这里我们只需要延伸 \(5\) hops 就够了。当然针对不同的图，可以延伸更广。用更数学的方式来描述的话就是

\[\begin{aligned} h_v^{(k)}&=\sigma(W^{(k)}\sum_{u\in N(v)}\frac{h_u^{(k-1)}}{|N(v)|}+B^{(k)}h_v^{(k-1)}) \\ H^{(l+1)}&=\sigma(H^{(l)}W_0^{(l)}+\tilde{A}H^{(l)}W_1^{(l)}) \end{aligned}\]

其中 \(\tilde{A}=D^{-\frac12}AD^{-\frac12}\)；\(W, B\) 就是我们需要训练的参数，可以将其理解为 neighbor 信息和 self 信息的一个 trade-off。在有了这个模型的情况下我们可以采用 supervised 以及 unsupervised。

unsupervised
不管是有监督还是无监督都需要损失函数，那这个损失函数从哪儿来？因为我们得到的是 embedding，因此可以使用一下几种方法

• random walks
• graph factorization
• node proximity in the graph

supervised
对于监督学习我们首先得提供训练数据，这个数据可以是整张图，也可以是一张很大的图的一部分导出子图。在训练数据上训练好模型后，就可以将这个模型应用到其他具有相似分布的图或者整张图的其他部分上去了。

GraphSAGE

现在还有一个遗留问题，即上面那张图中的方框代表什么？这其实是我们聚合邻接点信息的函数，这个函数可以是 sum，mean，pooling 等。也就是说我们可以将从邻接点得到的信息进行累加，平均，池化甚至可以在这里再嵌套一个神经网络，比如 LSTM。这一切都取决于你的应用以及效果。
GraphSAGE 其实就是一种图卷积网络，只不过它相比于 GCN 泛化了聚合操作。GraphSAGE 直接将邻接点信息和节点的自身信息进行拼接，并对节点的 embedding 加上了 l2-norm

\[h_v^{(k)}=\sigma([A^{(k)}\cdot AGG(\{h_u^{(k-1)},\forall u\in N(v)\}), B^{(k)}h_v^{(k-1)}]) \]

这里加入 LSTM 会违背 permutation invariant 的性质，但如果我们在给训练集的时候对每个节点的邻接点进行多次 shuffle，那么就没问题。

贴一张 slide，上面列举了很多 GNN 相关的应用。

Graph Attention Network

上面的 GCN 和 GraphSAGE 虽然在 AGG 函数上绞尽脑汁，但最终还是给所有邻接点相同的权重。如果现在我们希望能学习邻接点上不同的侧重，即给不同邻接点不同的权重，那么就需要用到 GAT。
现在定义 \(\alpha_{vu}\)，其中 \(u\in N(v)\) 代表了节点 \(v\) 到其邻接点的权重。同时定义 attention coefficients \(e_{vu}=a(W^{(k)}h_u^{(k-1)},W^{(k)}h_v^{(k-1)})\) 代表了 \(v\) 的邻接点 \(u\) 对 \(v\) 的重要性。那么 \(e_{vu}\) 和 \(\alpha_{vu}\) 的关系就是

\[\alpha_{vu}=\frac{\exp(e_{vu})}{\sum_{k\in N(v)}\exp(e_{vk})} \]

那么将这个 \(\alpha_{vu}\) 加入 GNN 就会得到 \(h_v^{(k)}=\sigma(\sum_{u\in N(v)}\alpha_{vu}W^{(k)}h_v^{(k-1)})\)。这样就完成了 GNN 中的 attention 机制。和一般的 attention 一样，这里也可以用 multi-head attention。

Tips

• data preprocessing is important
  • renormalization
  • variance-scaled
  • network whitening
• optimizer: adam
• activation: ReLU
• include bias in every layer
• GCN layer of size \(64\) or \(128\) is already plenty
• overfit on training set

Deep Generative Models for Graphs

上面讲了如何将图中的节点进行编码，那与之对应的就是解码了。这里的解码抽象地理解就是生成一张图。之前也有讲过类似 E-R、Small-World、Kronecker 图以及图的零模型等，但这些生成图的方法都很简单不具有普适性。我们想要一种给定一类图就能生成类似的图的模型。
要提出一个生成图的模型，首先需要明确几个困难点

1. 如果用邻接矩阵表示，那对于一个有 \(n\) 个节点的图，需要 \(n^2\) 的参数
2. 由于节点编号的原因，同样的图可能有 \(n!\) 种表示
3. 节点间的边可能会产生很复杂的依赖关系，例如生成一个环需要数所有节点的个数

那么将图的生成模型用更数学的方式表达就是在给定一些从分布 \(p_{data}(G)\) 中采样得到的图，我们需要让模型学习一个 \(p_{model}(G)\)，使得这个分布接近给定的分布。然后我们就可以从模型学习到的分布得到新的图。
如何使 \(p_{model}(x;\theta)\) 接近 \(p_{data}(x)\) 呢？很简单，极大似然

\[\theta^*=\argmax_{\theta}E_{x\sim p_{data}}\log p_{model}(x|\theta) \]

有了模型后我们怎么通过它得到新的图呢？

1. 从一个简单的噪声分布采样 \(z_i\sim N(0,1)\)
2. 通过一个函数将噪声种子转换为图 \(x_i=f(z_i;\theta)\)

而这里的 \(f(\cdot)\) 可以是神经网络。

GraphRNN: a Auto-Regressive Models

Auto-regressive 模型的特点是基于过去的行为预测未来的行为。这也就是接下来要讲的 GraphRNN 的工作原理。不过在此之前先回忆一下链式法则

\[p_{model}(x;\theta)=\prod\limits_{t=1}^np_{model}(x_t|x_1,...,x_{t-1};\theta) \]

在这儿的话 \(x_t\) 指我们采取的第t个操作 (加节点，加边)
对于节点顺序的问题，我们先假设它是固定的，后面会说到怎么编排顺序。那么在给定顺序后，生成图的序列定义为 \(S^{\pi}=(S_1^{\pi},S_2^{\pi},S_3^{\pi},...)\)。而每一项又是一个子序列，表示新加入的节点生成与之前节点连接的边的序列。即这里有两种序列 node-level 和 edge-level。这两个 level 之间相互依赖互相更新

• Node-level: 生成节点状态，并作为 edge-level 的初始状态
• Edge-level: 为新加入的节点生成边，并用生成的结果更新 node-level 的状态

但是如图中这样，将 edge-level 生成的结果直接输入下一个 cell 的话会使这个过程是 deterministic 的。因此为了引入随机性，将 edge-level 的输出变成概率，然后再输入下一个 cell 时进行 sampling。
训练时只需要用 ground truth 替换概率并用 binary cross entropy 计算损失来更新参数。

EOS (end of sequence) 在这里可以当做一个单独的状态，然后让模型在训练的时候学习它。在推理的时候让 node-level RNN 在 EOS 处停止；问题就是 edge-level 时是固定长度还是 EOS 停止？如果是 EOS 停止，那如果长度不够/超过了怎么办？

Tractability

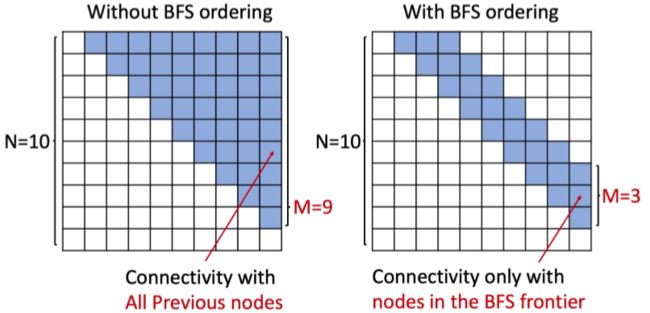
那么现在回到节点顺序的问题上。如果节点顺序没有排好就可能会出现后生成的节点与最初生成的节点有连接，即过于复杂的依赖。随着图的规模增加，这样可能会造成梯度消失或信息丢失。因此我们用最简单也最直观地方法解决排序问题：BFS。因为 BFS 的 breadth 的性质，它能很好的将图“分层”。

• 减少可能的排列组合
• 减少生成边时“回顾”长度