七天LeetCode刷题总结
- 引言
- 2019/1/26:两数之和
- 问题说明
- 完整代码
- 总结
- 2019/1/28:寻找两个有序数组的中位数
- 问题说明
- 问题分析
- 完整代码
- 总结
- 2019/1/29:最长回文子串
- 问题说明
- 最大公共子序列介绍与求解
- 问题分析
- 问题分析二
- 完整代码
- 总结
- 2019/1/30:字符串转换整数 (atoi)
- 问题分析
- 完整代码
- 总结
- 2019/1/31:最长公共前缀
- 问题分析与代码
- 总结
- 2019/2/1:三数之和
- 问题说明
- 思路分析与代码
- 总结
- 2019/2/2:最接近的三数之和
- 问题分析与代码
- 总结
引言
从今天起,为期7天LeetCode刷题记录。
2019/1/26:两数之和
问题说明
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
完整代码
那么我们就可以给出我们的解答,直接暴力:
class Solution:
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
if target < 2:
return None
for i in range(0,len(nums)-1):
for j in range(i+1,len(nums)):
if nums[i] + nums[j] == target:
return i,j
最后得出来的结果是10264 ms,好吧,双重for循环挺容易想的,但复杂度也高。然后我马上就想到了第二种:
class Solution:
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
if not nums:
return None
i = 0
while i < len(nums):
j = i + 1
difference = target - nums[i]
while j < len(nums):
if nums[j] == difference:
return i, j
j += 1
i += 1
结果是9564 ms。。。只比第一种好那么一点点,但我觉得比第一种考虑的东西多了很多,另外复杂度我本来想着是能降两个千的。可惜,好像还是暴力了,感觉太年轻。。。然后去看了下大佬的代码,发现要用字典做:
class Solution:
def twoSum(self, nums, target):
if not nums:
return None
d = dict()
for i, item in enumerate(nums):
tmp = target - item
if tmp in d:
return [i, d[tmp]]
d[item] = i
return None
总结
总结:这次时间上来讲,有点急,家里有些事,晚上才开始刷,白天在弄美赛和另一篇博文,所以导致两种方法间隔半小时,接下来要好好规划一下时间了。
2019/1/28:寻找两个有序数组的中位数
问题说明
很抱歉的是,2019/1/27号并没有刷题,由于家里有一些饭局以及美赛已经到了比较刺激的时候,虽然最后还是划了一天的水,但我竟然用2016年小区模拟的MATLAB自动机代码去模拟了一条龙的生长,至于生长公式,那不就跟造火箭是一个性质的嘛。。。最后结果跑是跑出来的,但完全不知道是个啥,守恒是不可能了,爱因斯坦也阻止不了龙族崛起。
最后写了个段子,参考知乎热榜2019年美赛是种什么体验:吸了一天的毒,又养了一天的龙,发现龙变成了喷火龙,并飞向了巴黎,所以,我想带你去浪漫的卢浮宫看一场恐怖袭击,顺便运用无人机进行空中救灾演习,虽然我仅仅只有虚拟货币,但还是想维持生态稳定性。
言归正传,其实这次美赛我没有参加,只是有种遗憾和情怀想再去玩一下而已,中途效率起伏不定,家里事也比较多,基本也算半玩半做吧,但目前已经没思路了,准备撤了,另外补齐一下昨天的刷题吧:
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
问题分析
这题可以写下分析,首先看到题目后面的难度为困难,说实话确实有点怕,代码水平不高,除了蓝桥杯还没做过困难的题,但没办法,眼看着又到交稿日期了,只能开干了,关于时间复杂度O(log(m + n)),不懂,没有学过数据结构,之前在一篇博文里总结过栈、队列和链表,我又回头看了一下,嗯,没啥用处。但时间复杂度是啥,没有太多概念,不过我好像在pythontop中刷过字符串转中位数的题,那么本题就有第一种解法了:
- 我希望将数组合并之后转换成字符串的格式,那么我就可以用之前的某道相似题做,这里大概就是用extend或者append合并,然后join得到结果,那么接下来就是字符串排序的问题了。但有一个问题就是,给的两个数组里的数据是整数,而不是字符串,后来我写程序写到一半,发现一直报错:TypeError: sequence item 0: expected str instance, int found,然后我搜狗了一下,发现join的seq参数需要要连接的元素序列、字符串、元组、字典。。。好吧,那里面还要转换,虽然可能可以转,用一些高级函数比如map,但不用想都知道时间复杂度已经超了,所以宣布暂停。
- 通过上面的一番调试,打消了我转换类型的想法,还是要规规矩矩的用列表进行得好,但我又发现(仔细看了遍题)这是两个有序列表,我突然想到了归并排序,这不就是归并的后两步嘛?让我们回想一下归并的步骤:
● 把长度为n的输入序列分成两个长度为n/2的子序列;
● 对这两个子序列分别采用归并排序;
● 将两个排序好的子序列合并成一个最终的排序序列。
这里就相当于归并算法,然后我顺便做了一个可视化:
所以,我直接以列表来排序不就行了?但我虽然感觉上是归并,但最后没有用归并。
没错,python里面还有更好的方式和归并等同,用一个内置函数,它里面的逻辑其实是用快排做的,那就是sort。如果忘了的朋友,可以看下我下面的这篇博文,不过这篇博文里我好像没提到这一点:
python内置函数总结与思维导图
完整代码
class Solution:
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
nums1.extend(nums2) # 合并
add = nums1
if not add:
return None
add.sort() # 改变原来的列表
if len(add) % 2: # 计数不是循环。
return add[len(add)//2] / 1.0
else:
return (add[len(add)//2] + add[(len(add)//2)-1]) / 2.0
总结
总结:这个代码总共提交了3次,每次结果都不一样,最好在112ms,这也是排序的特性。另外需要注意sort和sorted的区别,如果是sorted需要赋给新的变量。然后我提交完后去查了下快排的时间复杂度,发现是O(nlogn),那么本题就应该是O((n+m)log(n+m))了,好像和题意有些出入?。。不太清楚,官方题解没有看懂,但感觉递归法应该可行,不过我暂时没想了,有些朋友一年没见了,今天天气也还好,要去碰个面,晚上回来可能继续造龙?。。。感觉有点悬,还是吸个毒造个火箭吧。(手动笑脸)
2019/1/29:最长回文子串
问题说明
嗯,要开始认真刷题了,最近一些事情算忙完了,接下来又是新的开始。那么话不多说,开始今天的题。
给定一个字符串
s,找到s中最长的回文子串。你可以假设s的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
题目意思相比于上题来讲,算很清楚了,但清楚的题目往往都不是很好做。然后鉴于现在时间还算充裕,我不知道这题对于暴力求解会不会超时,但暂时没想用了,有时候一味暴力容易陷入死局,大概看了一下官方题解,这个也比上题清晰,甚至有点太过笼统。。从动态规划到中心扩展算法,最后是Manacher,嗯,不懂。然后今天主要研究了一下动态规划。下面为分析:
最大公共子序列介绍与求解
可能本题我有点跑偏,因为之前确实没怎么看过动态规划这方面的东西,但无关大雅,作为动态规划里最经典的案例之一,最大公共子序列(Longest Common Subsequence,简称LCS),是从两个公共的序列中提取相同的子序列,子序列是指从原序列中任意去掉若干元素(不一定连续)的序列,本题因为是字符串,那么我们两段序列也为字符串,举个例子: S S S 为"abccade", J J J 为"dgcadde",那么它们的最长公共子串即为"cad"。
对于上面这个例子,可能我们想到的最简单的方法是采用蛮力法,假设字符串 S S S 与 J J J 的长度分别为 l e n 1 len1 len1 和 l e n 2 len2 len2 (假设 l e n 1 len1 len1 >= l e n 2 len2 len2 )。那么可以先找出 J J J 的所有可能子串,然后判断这些子串是否也是 S S S 的子串,但效率非常低下,原因是比较次数过多,那么动态规划就是一种能通过减少比较次数从而降低时间复杂度的方法。
那么,什么是动态规划?动态规划算法通常基于一个递推公式及一个或多个初始状态。当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度,因此它比回溯法、暴力法等要快许多。
根据上面的意思,如果要运用动态规划来解决这个问题,首先我们要构造递归关系。假设 L C S [ i , j ] LCS[i,j] LCS[i,j]为序列 S [ 1.. i ] S[1..i] S[1..i] 和 J [ 1.. j ] J[1..j] J[1..j] 的LCS长度,那么我们是否可以用更小的实例来求解 L C S [ i , j ] LCS[i,j] LCS[i,j] 呢?我们可以减少序列的长度,可能的子问题是 L C S [ i − 1 ] [ j ] , L C S [ i ] [ j − 1 ] , L C S [ i − 1 ] [ j − 1 ] LCS[i-1][j], LCS[i][j-1], LCS[i-1][j-1] LCS[i−1][j],LCS[i][j−1],LCS[i−1][j−1],那么 L C S [ i ] [ j ] LCS[i][j] LCS[i][j]是否与这些子问题有关呢?这里还需要考虑 S [ i ] S[i] S[i]与 J [ j ] J[j] J[j],我们分情况讨论:
- S [ i ] = J [ j ] S[i] = J[j] S[i]=J[j]时,此时两个元素匹配,得到最优解。假如想让 S [ i ] S[i] S[i]与 J [ j ] J[j] J[j]匹配之前的元素,那么就需要保证下一次的匹配结果不能差于本次结果,所以最优情况是让两者匹配,那么 L C S [ i ] [ j ] LCS[i][j] LCS[i][j]就依赖于 L C S [ i − 1 ] [ j − 1 ] LCS[i-1][j-1] LCS[i−1][j−1]:
L C S [ i ] [ j ] = 1 + L C S [ i − 1 ] [ j − 1 ] LCS[i][j] = 1 + LCS[i-1][j-1] LCS[i][j]=1+LCS[i−1][j−1] - S [ i ] ≠ J [ j ] S[i] \ne J[j] S[i]̸=J[j]时,此时相当于去掉 S [ i ] S[i] S[i]或 J [ j ] J[j] J[j],其分别对应于求解 L C S [ i − 1 ] [ j ] LCS[i-1][j] LCS[i−1][j]和 L C S [ i ] [ j − 1 ] LCS[i][j-1] LCS[i][j−1],所以 L C S [ i ] [ j ] LCS[i][j] LCS[i][j]可以取两者的最大值:
L C S [ i ] [ j ] = m a x ( L C S [ i − 1 ] [ j ] , L C S [ i ] [ j − 1 ] ) LCS[i][j] = max(LCS[i-1][j], LCS[i][j-1]) LCS[i][j]=max(LCS[i−1][j],LCS[i][j−1])
由此,我们可以根据上面的式子得到 L C S [ i ] [ j ] LCS[i][j] LCS[i][j]所有的值,进而找出最长的子串,另外关于上面我举的 S S S 为"abccade"、 J J J为"dgcadde"的例子,我们可以画出动态规划的计算结果,为:
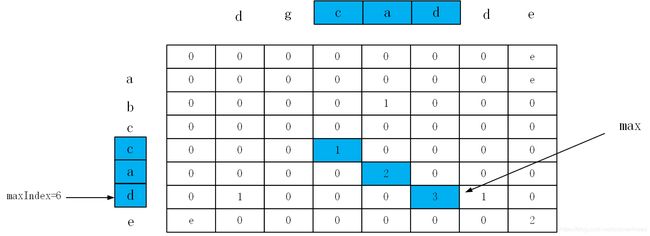
可能有点小丑,但无伤大雅。通过上图所示,max为最长公共子串的长度,以及maxIndex为最长子串结尾字符在字符数组中的位置,由这两个值就可以确定最长公共子串为"cad",实现代码参考python算法面试宝典,如下:
"""
方法功能:获取两个字符串的最长公共字串
输入参数:str1和str2为指向字符的引用(指针)
"""
def getMaxSubStr(str1,str2):
len1 = len(str1)
len2 = len(str2)
SJ = ''
maxs = 0 # 用来记录最长公共子串的长度
maxI = 0 # 用来记录最长公共字串最后一个字符的位置
"""申请新的空间来记录公共字符长度信息"""
M = [[0 for i in range(len1 + 1)] for j in range(len2 + 1)]
"""利用递归公式构建二维数组"""
i = 0
while i < len1 + 1:
M[i][0] = 0
i += 1
j = 0
while j < len2 + 1:
M[0][j] = 0
j += 1
i = 1
"""动态规划推导"""
while i < len1 + 1:
j = 1
while j < len2 + 1:
if list(str1)[i-1] == list(str2)[j-1]:
M[i][j] = M[i-1][j-1] + 1
if M[i][j] > maxs:
maxs = M[i][j]
maxI = i
else:
M[i][j] = 0
j += 1
i += 1
"""找出公共子串"""
i = maxI - maxs
while i < maxI:
SJ = SJ + list(str1)[i]
i += 1
return SJ
问题分析
参照上面的理解,那么我可以将 J J J变为 S S S的逆序,图解为:
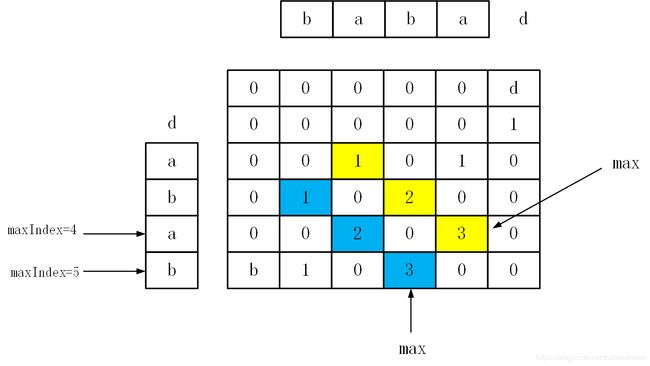
意思是一样的,然后我改完代码之后在本地跑是可以实现的,除了时间长点以外,但我带入LeetCode提交后它显示一些莫名的报错信息,输入babad,我的代码输出结果为a?如果是爆内存还说得过去,但这判定好像有问题吧。。本地为bab,一切正常,我。。无话可说咯
问题分析二
中途看了下光城的微信公众号对于本题的理解以及代码,然后我再加上了点我自己的理解,那么分析如下:
如果要判断一个字符串是否是一个回文子串,还是可以参照上面我画的图,这里会有三种情况:
第一种:当所检测的子串长度为1时,即行列相等,那么可以说这是一个回文数;
第二种:当所检测的子串长度为2时,只需要判断当前与下一个元素是否相等即可确定该子串是否是回文串;
第三种:当所检测的子串长度为3即以上时,直接以3为跨步,便可以访问到每个子串的末尾字符,那么当当前位置的字符与末尾字符相等时,并且通过访问之前已经存储过的True or False进行比对,我们可以得到状态转移方程为:
d p [ i ] [ j ] = { t r u e , s t r [ i ] = = s t r [ j ] a n d d p [ i + 1 ] [ j − 1 ] = = t r u e ∣ 1 f a l s e dp[i][j] = \left\{\begin{matrix} true,str[i]==str[j] \ and \ dp[i+1][j-1]==true|1 & \\ false & \end{matrix}\right. dp[i][j]={true,str[i]==str[j] and dp[i+1][j−1]==true∣1false
完整代码
class Solution:
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
# 获取字符串的长度
s_len = len(s)
# 生成dp算法的二维数组,即额外的存储空间记录要查找得历史信息
dp = [[0] * s_len for i in range(s_len)]
if s_len == 0:
return s
# 最大长度
maxLen = 1
# 第一种:检查目标子串长度为1,并初始化长度为1的回文字符串信息
i = 0
while i < s_len:
dp[i][i] = True
i += 1
# 第二种:检查目标子串长度为2,并初始化长度为2的回文字符串信息
start = 0
i = 0
while i < s_len - 1:
if s[i] == s[i + 1]:
dp[i][i + 1] = True
start = i
maxLen = 2
i += 1
# 第三种:检查目标子串长度为大于等于3
# 遍历长度
pal_num = 3
while pal_num <= s_len:
i = 0
# 表示循环子串长度为pal_num时,有n-pal_num+1种组合
while i < (s_len - pal_num + 1):
# 定义子串末尾
j = i + pal_num - 1
# 只有再中间的数为True且两边一样的情况下,才可以将其作为回文子串
if s[i] == s[j] and dp[i + 1][j - 1]:
dp[i][j] = True
if pal_num > maxLen:
start = i
maxLen = pal_num
i += 1
pal_num += 1
return s[start:start + maxLen]
总结
没有啥太大总结的,关于本题,目前就只总结了关于动态规划版本的,不过我查到的很多博文里,解法还有很多,manacher、二叉树搜索、中心扩展等等,暂时还不会,先放在这里,如果以后有时间会总结的。
2019/1/30:字符串转换整数 (atoi)
因为本题题目太长,还有我本篇博客好像写得也有点长了,所以为了节省空间,那我就直接切入主题吧,题目见:
https://leetcode-cn.com/problems/string-to-integer-atoi/
问题分析
看完题目后我们需要知道,题目以及示例透露出了几个关键点,首先是对于字符串,字符串的格式类型转换的函数有哪些,弄清楚了这个再看看示例,很明显示例为3个约束条件,分别是有无空格,正负号和边界检测,那么我们就可以对此进行详细分析:
- 过滤掉字符串两头的一个或多个空格,用strip()函数实现;当然,我们还可以使用lstrip表示去除句首的空格,rstrip表示句尾,另外还能用join(" “,”")直接去掉所有空格,这些都是可以的,但方法都需要做相应的改变罢了;
- 去了空格,根据上面的提示,就需要判断正负号,所以当第一个字符不为空时,判断第一个字符是否为+/-,即获取并保存正负号sign
- 遍历字符串,如果子串仅仅包含连续的0~9之间的数字,那么记录该子串并转换为数字,一旦发现非数字字符,直接退出循环;
- 将得到的数字成上正负号,并对最终结果做边界检测
完整代码
#coding:utf-8
class Solution(object):
def myAtoi(self, s):
"""
:type str: str
:rtype: int
"""
str = s.strip()
sign = 1
num = 0
if not str:
return 0
if str[0] == "-":
sign = -1
elif str[0] == "+":
sign = 1
str = str[1:]
for ch in str:
if ch >= "0" and ch <= "9":
num = num * 10 + ord(ch) - ord('0')
else:
break
num = num * sign
if num > 2 ** 31 - 1:
return 2 ** 31 - 1
elif num < -2 ** 31:
return -2 ** 31
else:
return num
a = Solution()
a1 = a.myAtoi("1234")
print(a1)
这题我感觉从思路来讲谁都会说,但真正写代码倒是会有很多意想不到的结果,而由于今天一天我都在乡下喝别人的喜酒,时间上耽误了不少,下午没事的时候拿纸和笔一边看一些人的博客,代码今天想得不久,主要是没有debug,然后一边也手推了些,另外关于上面的代码,我就解释一下num = num * 10 + ord(ch) - ord(‘0’)了:
“1234” =〉 1234
从头开始解析
首先是1
然后110+2 = 12
1210+3 = 123
123*10+4 = 1234
总结
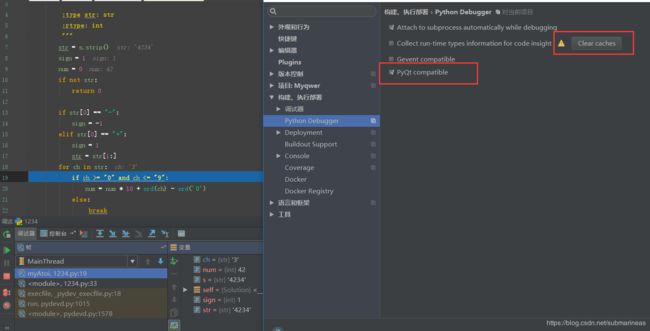
晚上接近9点半回,然后回来写博客,中途发现了一个意想不到的事情,当我在对程序打断点调试的时候,发现了如下错误:
pydev debugger: process 4228 is connecting
Connected to pydev debugger (build 171.3780.47)
1234
也就是说进入不了调试界面,然后大概看了下网上的方法,试了很多种,有说清空Invalidate Caches / Restart,即设置里面的缓存信息,还有重新配置工程什么的,好像基本都没有用,后来发现是pyqt compatable的问题,我认为正确的解法应该是pyqt compatable 选择了auto ,pyqt5不兼容,PyQt4 或 PySide 二者选其一即可。但我的pycharm应该是我之前换系统太频繁而pycharm一直没有卸载重装,另外环境也是虚拟环境,所以这里应该默认是auto吧。。于是我取消了勾选,然后又开启了勾选之后,奇迹般的好了。。这里记录一下。
2019/1/31:最长公共前缀
问题分析与代码
算法二:水平扫描
算法
想象数组的末尾有一个非常短的字符串, 使用上述方法依旧会进行S次比较。 优化这类情况的一种方法就是水平扫描。 我们从前往后枚举字符串的每一列,先比较每个字符串相同列上的字符(即不同字符串相同下标的字符)然后再进行对下一列的比较。
上面的解释其实是LeetCode官方给出来的解释,然后我大概看着它的Java代码写出来的python版,中途有很多小坑,比如说我习惯性输None,这里却要求是"",题目示例太少,测试示例太坑,所以我没少放错。。
class Solution:
def longestCommonPrefix(self, strs):
"""
:type strs: List[str]
:rtype: str
"""
if not strs:
return ""
for i in range(len(strs[0])):
for j in range(len(strs)):
if i > len(strs[j])-1 or strs[j][i] != strs[0][i]:
if i==0:
return ""
else:
return strs[0][:i]
return strs[0]
a = ["flower","flow","flight"]
str = Solution()
c = str.longestCommonPrefix(a)
print(c)
# 测试用例还有[""],["aa","a"],["a"]好像是这些错误吧。
总结
虽然官方给出了很多种解释,但目前我想的就一种,因为我好像又很久没更新博文了,本篇是总结,看情况下午要为下一篇博文做准备,还有就是统计学也要开始总结,原计划的英语还是没变,在下个礼拜。
2019/2/1:三数之和
问题说明
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
思路分析与代码
首先拿到这个题目,我的第一想法是暴力。没错,简而言之,和前面几题的思路类似,遇事不决先暴力,暴力无解再分析,分析无路看题解,题解看懂齐代码。顺便编了一手打油诗。
另外,根据前面几题的教训,让我深刻知道了注意事项的重要性,因为测试用例一定会体现出来,所以写出的第一版暴力代码为:
class Solution:
def threeSum(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
a = sorted(nums)
list1 = []
for i in range(len(a)-1):
for j in range(i+1,len(a)-1):
for k in range(j+1,len(a)):
if i != j and i != k and j != k and a[i] + a[j] + a[k] == 0:
num = [a[i],a[j],a[k]]
if num not in list1:
list1.append(num)
return list1
这里的复杂度大概就是在n**3间了,然后我大概也预料到了提交会超时,果然测试用例是卡在倒数第三个,然后开始想第二版针对这个时间复杂度进行优化的代码。
第二种思路想了一段时间,这次是想如果a + b = -c,那么只要循环两次,但后来写代码硬是没有调试出来。。太弱了,最后看了下别人的代码,突然又看了下第一题,回想起第一题的总结,太年轻了!!
class Solution:
def threeSum(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
nums.sort()
res = set()
for i,v in enumerate(nums[:-2]):
d = {}
for x in nums[i+1:]:
if x not in d:
d[-v-x] =1
else:
res.add((v,-v-x,x))
return list(res)
总结
题目刚做了一个礼拜不到就忘了坑?感觉还是代码量不够,字典用得不熟,需要时常总结。
2019/2/2:最接近的三数之和
没啥说的,题目和上题差不多,算是变种题。但上题没用分而治之的方法,算是取了个巧,所以这题探究一下。
问题分析与代码
什么是分而治之?我的理解是先控制一个位置固定,然后对其余两个位置“左右夹逼”,再将这个固定的位置移动,然后“左右夹逼”。并以此类推,那么这题也是一样,先设定三个指针left, mid, right。初始时,left为数组最左端的元素,且固定不变,mid = left + 1, right为数组最右端的元素。然后对 left, mid, right三个指针所指向的值求和,记为res. 然后是完整代码,这里是照着LeetCode的解答方案中,选择了一种和我想得差不多的仿写了一下,虽然我知道是这样做,但真正写代码还是有点难。
class Solution:
def threeSumClosest(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
nums.sort()
if len(nums)<3:
return None
res=abs(nums[0]+nums[1]+nums[-1]-target)
res1=[]
if res==0:
return target
for i in range(len(nums)):
l=i+1
r=len(nums)-1
while l<r:
temp=nums[i]+nums[l]+nums[r]
if abs(temp-target)<=res:
res=abs(temp-target)
res1=temp
if temp<target:
l+=1
elif temp>target:
r-=1
else:
return target
return res1
总结
所以,到此为止,7天的LeetCode之旅就此结束了,我算是用记日记的方式编辑了7天,期间经历了各种各样的外界因素与自己本身心态的调整。因为快过年了,家里比较忙,自己有时候心里也比较浮躁。另外需要考虑的也很多,除了刷题LeetCode,还有扇贝单词和统计学习方法每天要动。所以难免有些力不从心,但或许只有这样,我才会感觉到自己还在路上,认识到自己的不足与逐步反思,并且有所收获。如果是看到这里的读者,也希望你们能有所收获,这应该就是我写博客的目的吧。