4.K均值算法--应用

1. 应用K-means算法进行图片压缩

读取一张图片

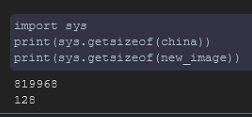
观察图片文件大小，占内存大小，图片数据结构，线性化

用kmeans对图片像素颜色进行聚类

获取每个像素的颜色类别，每个类别的颜色

压缩图片生成：以聚类中收替代原像素颜色，还原为二维

观察压缩图片的文件大小，占内存大小

例题：

'''
K-Means算法应用：图片压缩(将颜色减少，相似的归为一类)
'''
from sklearn.datasets import load_sample_image
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np

china = load_sample_image("china.jpg")
# image = china[::3, ::3]
X = china.reshape(-1, 3)
# print(china.shape, image.shape, X.shape)
print(china.shape, X.shape)

n_colors = 64  # (255, 255, 255)
model = KMeans(n_colors)
labels = model.fit_predict(X)
colors = model.cluster_centers_  # 二维(64, 3)
new_image = colors[labels].reshape(china.shape) # （143，214，3）

plt.imshow(china)
plt.show()
plt.imshow(new_image.astype(np.uint8))
plt.show()
plt.imshow(new_image.astype(np.uint8)[::3, ::3])
plt.show()

 

作业：

 1 '''
 2 1. 应用K-means算法进行图片压缩
 3 读取一张图片
 4 观察图片文件大小，占内存大小，图片数据结构，线性化
 5 用kmeans对图片像素颜色进行聚类
 6 获取每个像素的颜色类别，每个类别的颜色
 7 压缩图片生成：以聚类中收替代原像素颜色，还原为二维
 8 观察压缩图片的文件大小，占内存大小
 9 '''
10 from sklearn.cluster import KMeans
11 from pylab import mpl
12 import matplotlib.pyplot as plt
13 import matplotlib.image as mpimg
14 import numpy as np
15 import sys
16 
17 # 解决中文无法显示
18 mpl.rcParams['font.sans-serif'] = ['SimHei']
19 
20 photo = mpimg.imread("D://小阔爱//大学课程//机器学习//K均值聚类算法//girl.jpg")
21 plt.title("原图")
22 plt.imshow(photo)
23 plt.show()
24
25 print("============原图片属性============")
26 print("尺寸：", photo.shape)  #显示尺寸
27 print("宽度：", photo.shape[0])  #图片宽度
28 print("高度：", photo.shape[1])  #图片高度 
29 print("通道数：", photo.shape[2])  #图片通道数
30 print("数据结构：", type(photo))  #显示类型
31 print("占用内存大小：",sys.getsizeof(photo))
32 print("总像素个数：", photo.size)   #显示总像素个数
33 print("最大像素值：", photo.max())  #最大像素值
34 print("最小像素值：", photo.min())  #最小像素值
35 print("像素平均值：", photo.mean())  #像素平均值
36 
37 '''
38 构建模型
39 '''
40 image = photo[::3, ::3]
41 # image.shape
42 x = image.reshape(-1, 3)
43 n_colors = 12  # 颜色类别
44 model = KMeans(n_colors)
45 '''
46 模型训练、预测
47 '''
48 labels = model.fit_predict(x)
49 colors = model.cluster_centers_  # 模型聚类中心
50 new_photo = colors[labels]  # 以聚类中收代替原像素颜色
51 new_photo = new_photo.reshape(image.shape)  # 还原为二维数组
52 
53 plt.title("压缩图")
54 plt.imshow(new_photo.astype(np.uint8))
55 plt.show()
56 print("============压缩后图片属性============")
57 print("尺寸：", new_photo.shape)  #显示尺寸
58 print("宽度：", new_photo.shape[0])  #图片宽度
59 print("高度：", new_photo.shape[1])  #图片高度 
60 print("通道数：", new_photo.shape[2])  #图片通道数
61 print("数据结构：", type(photo))  #显示类型
62 print("占用内存大小：",sys.getsizeof(new_photo))
63 print("总像素个数：", new_photo.size)   #显示总像素个数
64 print("最大像素值：", new_photo.max())  #最大像素值
65 print("最小像素值：", new_photo.min())  #最小像素值
66 print("像素平均值：", new_photo.mean())  #像素平均值
67 new_photo = new_photo.astype(np.uint8)
68 img.imsave("D://小阔爱//大学课程//机器学习//K均值聚类算法//new_girl.jpg", new_photo)

 

 

2. 观察学习与生活中可以用K均值解决的问题。

从数据-模型训练-测试-预测完整地完成一个应用案例。

这个案例会作为课程成果之一，单独进行评分。

　　场景：银行希望为其客户提供信用卡优惠

　　已有：每个客户详细信息

　　期望：根据已有信息，能够决定向哪个客户提供对应性优惠

　　众所周知，银行所拥有的客户量数据十分庞大，人为查看客户信息向其推送合适的信用卡优惠显然是无稽之谈。这时，可以利用K-Means聚类算法对客户进行不同群体分类，即将客户划分为不同的组，如下图：

　　

 　　当客户被分类后，银行便可以根据客户收入的高低决定实施的优惠类型，假设是上图中的三种收入水平，那么银行只需要制定三种不同的优惠策略。

　　本案例将以银行客户信息记录作为数据集，使用K-Means聚类算法获取客户价值，数据集中包括客户的性别、接受教育程度、收入以及债务等13条属性信息。

　　识别客户价值应用此处选用2个指标：

• Loan Amount（债务总数）
• ApplicantIncome（申请人收入）

1.导入数据集，查看数据

1 # 读取数据
2 cluster_data = pd.read_csv("./data/clustering.csv", encoding='utf-8')
3 cluster_data.head()

数据集原始数据：

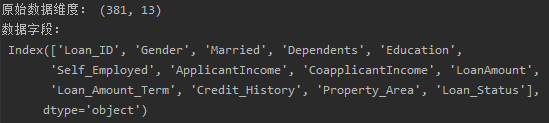
2.查看数据集有多少记录以及字段，并罗列出来（方便后续判断）

1 print("原始数据维度：", cluster_data.shape)
2 print("数据字段：\n", cluster_data.columns)

总共有381行记录，13个字段：

 3.确定Loan Amount（债务总数）、ApplicantIncome（申请人收入）为指标。

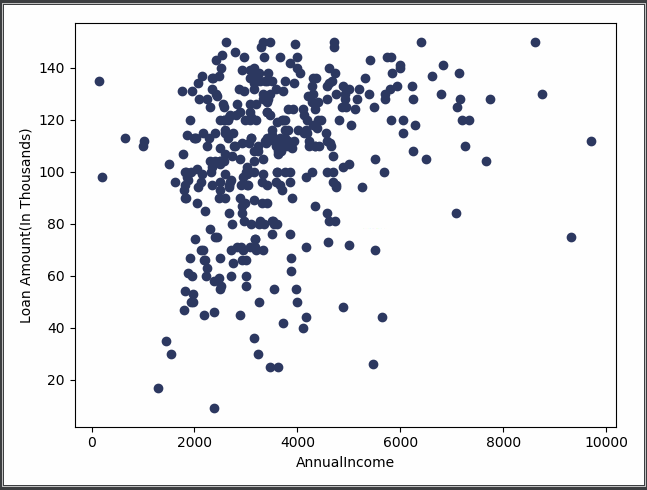
 1 '''
 2 选择LoanAmount与ApplicantIncome作为可视化据点，
 3 利用散点图将其画出，观察二者关系
 4 '''
 5 import matplotlib.pyplot as plt
 6 
 7 x = cluster_data[['LoanAmount', 'ApplicantIncome']]
 8 plt.scatter(x['ApplicantIncome'], x['LoanAmount'], c='#2D3961')
 9 plt.xlabel("AnnualIncome")
10 plt.ylabel("Loan Amount(In Thousands)")
11 plt.show()

　　下图是以ApplicantIncome（申请人收入）为横坐标，Loan Amount（债务总数）为纵坐标制作的散点图，能够直观看出客户债务以及收入之间的关系。但是无法看出客户群体类别。

  

4.选取最优K值

　　手肘法的核心思想是：随着聚类数k值的增大，样本划分会更加精细，每个簇的聚合程度逐渐提高，与此同时，误差平方和SSE逐渐变小。当k值小于真实聚类数时，k的增大会大幅度增加每个簇的聚合程度，故而SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度会迅速变小，所以SSE的下降幅度会骤减，而后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。

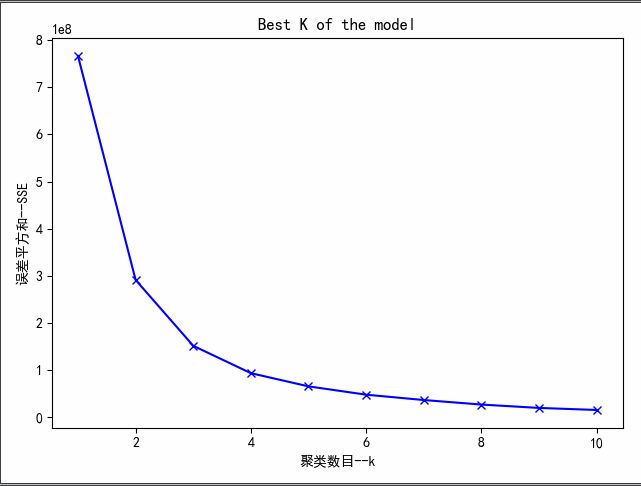
　　在本案例中，我将采用手肘法对K值进行选取，代码如下：

 1 '''
 2 确定最优聚类数目--手肘法
 3 '''
 4 n_clusters = range(1, 11)
 5 SSE = []
 6 for k in n_clusters:
 7     estimator = KMeans(n_clusters=k)  # 构造聚类器
 8     estimator.fit(x)
 9     SSE.append(estimator.inertia_)
10 plt.xlabel("聚类数目--k")
11 plt.ylabel("误差平方和--SSE")
12 plt.plot(n_clusters, SSE, 'bx-')
13 plt.title('Best K of the model')
14 plt.show()

　　显然，肘部对于k值而言，3是最优聚类数目。

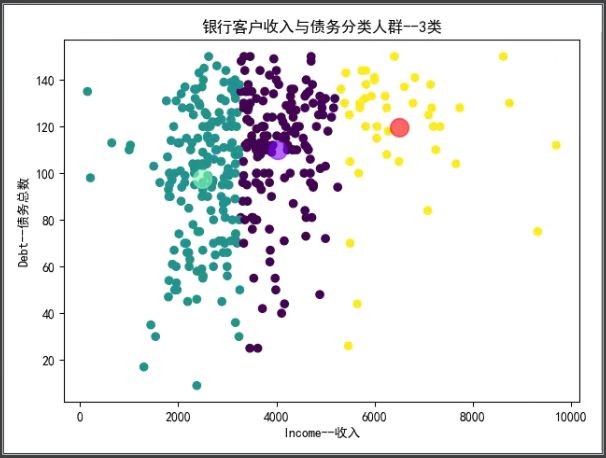
4.确定k值选取后，需要利用K-Means聚类算法对这些客户群体进行分组，并使其分类后以不同颜色展示出来。

 1 '''
 2 利用K-Means聚类算法对客户群体进行分类
 3 '''
 4 from sklearn.cluster import KMeans
 5 # 处理中文显示问题
 6 plt.rcParams['font.sans-serif'] = 'SimHei'
 7 plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号
 8 
 9 k = 3  # 选取聚类中心
10 KMeans_model = KMeans(n_clusters=k)  # 构建模型
11 KMeans_model.fit(x)  # 训练模型
12 y_pre = KMeans_model.predict(x)  # 测试模型
13 kmeans_centers = KMeans_model.cluster_centers_  # 聚类中心
14 # print(kmeans_centers[0], kmeans_centers[1])
15 kmeans_labels = KMeans_model.labels_  # 样本中的类别标签
16 plt.scatter(x['ApplicantIncome'], x['LoanAmount'], c=y_pre)
17 plt.scatter(kmeans_centers[:, 1], kmeans_centers[:, 0], c=[1, 2, 3], 
18             s=200, alpha=0.6, cmap='rainbow')
19 20 plt.title("银行客户收入与债务分类人群--3类")
21 plt.xlabel("Income--收入")
22 plt.ylabel("Debt--债务总数")
23 plt.show()