并查集详解与应用

【导引问题】
题目描述：
某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？

输入：
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说

3 3
1 2
1 2
2 1

这种输入也是合法的
当N为0时，输入结束，该用例不被处理。

输出：

    对每个测试用例，在1行里输出最少还需要建设的道路数目。

样例输入：

4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

样例输出：

1
0
2
998

【概念】
英文：Disjoint Set，即“不相交集合”将编号分别为1…N的N个对象划分为不相交集合，
在每个集合中，选择其中某个元素代表所在集合。常见两种操作：
合并两个集合查找某元素属于哪个集合所以，也称为“并查集”
我们先来看如下的数字集合：集合 A{1,2,3,4}，集合 B{5,6,7}，集合 C{8,0}
我们利用如下树结构来表示这些集合：

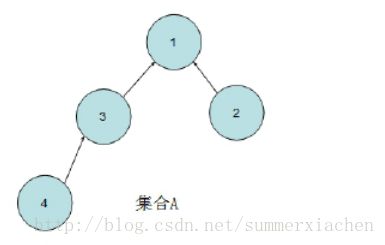
如图所示，我们用一棵树上的结点来表示在一个集合中的数字，要判断两个数字是否在一个集合中，我们只需判断它们是否在同一棵树中。那么我们使用双亲结点表示法来表示一棵树，即每个结点保存其双亲结点。若用数组来表示如上树，则得到如下结果：

即我们在数组单元 i 中保存结点 i 的双亲结点编号，若该结点已经是根结点则其双亲结点信息保存为-1。有了这样的存储结构，我们就能通过不断地求双亲结点来找到该结点所在树的根结点，若两个元素所在树的根结点相同，则可以判定它们在同一棵树上，它们同属一个集合。
对于合并两个集合的要求，我们该如何操作呢？我们只需要让分别代表两个集合的两棵树合并，合并方法为其中一棵树变为另一棵树根结点的子树，如下图所示：

如图，若我们对 2 所在的集合与 0 所在的集合合并，则先找到表示 2 所在集合的树的根结点 1 和表示 0 所在集合的树的根结点 4，并使其中之一（图中为 4）为另一个根结点的儿子结点，这样其中一棵树变为另一棵树根结点的一棵新子树，完成合并。在双亲结点表示法中，该合并过程为：

但是，采用这种策略而不加以任何约束也可能造成某些致命的问题。如前文所述，我们对集合的操作主要通过查找树的根结点来实现，那么并查集中最主要的操作即查找某个结点所在树的根结点，我们的方法是通过不断查找结点的双亲结点直到找到双亲结点不存在的结点为止，该结点即为根结点。那么，这个过程所需耗费的时间和该结点与树根的距离有关，即和树高有关。在我们合并两树的过程中，若只简单的将两树合并而不采取任何措施，那么树高可能会逐渐增加，查找根结点的耗时逐渐增大，极端情况下该树可能会退化成一个单链表。为了避免因为树的退化而产生额外的时间消耗，我们在合并两棵树时就不能任由其发展而应该加入一定的约束和优化，使其尽可能的保持较低的树高。为了达到这一目的，我们可以在查找某个特定结点的根结点时，同时将其与根结点之间所有的结点都直接指向根结点，这个过程被称为路径压缩，如下图所示：

【分析】
定义一个数组，用双亲表示法来表示各棵树（所有的集合元素个数总和为 N）：int Tree[N];
用 Tree[i]来表示结点 i 的双亲结点，若 Tree[i]为-1 则表示该结点不存在双亲结点，即结点 i 为其所在树的根结点。
那么，为了查找结点 x 所在树的根结点，我们定义以下函数：

int findRoot(int x) {
if (Tree[x] == -1) return x; //若当前结点为根结点则返回该结点号
else return findRoot(Tree[x]); //否则递归查找其双亲结点的根结点
}

这里我们将查找函数写成了递归的形式，不熟悉递归的读者可以参考如下非
递归形式的函数：

int findRoot(int x) {
int ret;
while (Tree[x] != -1)
x = Tree[x]; //若当前结点为非根结点则一直查找其双亲结点
ret = x; //返回根结点编号
return ret;
}

另外若需要在查找过程中添加路径压缩的优化，我们修改以上两个函数为：

int findRoot(int x) {
if (Tree[x] == -1) return x;
else {
int tmp = findRoot(Tree[x]);
Tree[x] = tmp; //将当前结点的双亲结点设置为查找返回的根结点编号
return tmp;
}
}

同样的，其非递归形式如下

int findRoot(int x) {
int ret;
int tmp = x;
while (Tree[x] != -1)
x = Tree[x];
ret = x;
x = tmp; //再做一次从结点x到根结点的遍历
while(Tree[x] != -1) {
int t = Tree[x];
Tree[x] = ret;
x = t; //遍历过程中将这些结点的双亲结点都设置为已经查找得到的根结点编号
}
return ret;
}

【问题分析】
题面中描述的是一个实际的问题，但该问题可以被抽象成在一个图上查找连通分量（彼此连通的结点集合）的个数，我们只需求得连通分量的个数，就能得到答案（新建一些边将这些连通分量连通）。
这个问题可以使用并查集完成，初始时，每个结点都是孤立的连通分量，当读入已经建成的边后，我们将边的两个顶点所在集合合并，表示这两个集合中的所有结点已经连通。
对所有的边重复该操作，最后计算所有的结点被保存在几个集合中，即存在多少棵树就能得知共有多少个连通分量（集合）。

#include
using namespace std;
#define N 1002
int Tree[N];
int findroot(int x)//找到x节点的根并压缩路径。 
{
    int root;
    int temp=x;
    while(Tree[x]!=-1)//找到x节点的根。 
    {
        x=Tree[x];
    }
    root=x;
    x=temp;
    //while(Tree[x]!=-1)与while(x!=root)等同 
    while(x!=root) //路径压缩 
    {
        int t=Tree[x];
        Tree[x]=root;
        x=t;
    }
    return root;
}
int main()
{
    int n,m;
    while(cin>>n)
    {
        if(n==0) break;
        cin>>m;
        for(int i=1;i<=n;i++)//初始化。 
            Tree[i]=-1;

        while(m--!=0)
        {
            int a,b;
            cin>>a>>b;
            a=findroot(a);
            b=findroot(b);
            if(a!=b)
            Tree[a]=b;
        }
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            if(Tree[i]==-1) ans++;
        }
        cout<1<