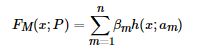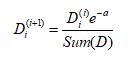bagging与boosting、Adaboost、Random Forest、GBDT、Xgboost
bagging与boosting区别
集成学习
集成学习通过构建并结合多个学习器来完成学习任务.只包含同种类型的个体学习器,这样的集成是“同质”的;包含不同类型的个体学习器,这样的集成是“异质”的.集成学习通过将多个学习器进行结合,常可获得比单一学习器显著优越的泛化性能.
根据个体学习器的生成方式,目前的集成学习方法大致可分为两大类,即个体学习器间存在强依赖关系、必须串行生成的序列化方法,以及个体学习器间不存在强依赖关系、可同时生成的并行化方法;前者的代表是Boosting,后者的代表是Bagging和“随机森林”.
bagging与boosting的概念及区别
首先介绍Bootstraping,即自助法:它是一种有放回的抽样方法(可能抽到重复的样本).
1、Bagging (bootstrap aggregating)
Bagging即套袋法,其算法过程如下:
A)从原始样本集中抽取训练集.每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本(在训练集中,有些样本可能被多次抽取到,而有些样本可能一次都没有被抽中).共进行k轮抽取,得到k个训练集.(k个训练集相互独立)
B)每次使用一个训练集得到一个模型,k个训练集共得到k个模型.(注:根据具体问题采用不同的分类或回归方法,如决策树、神经网络等)
C)对分类问题:将上步得到的k个模型采用投票的方式得到分类结果;对回归问题,计算上述模型的均值作为最后的结果.
2、Boosting
Boosting是一族可将弱学习器提升为强学习器的算法.
关于Boosting的两个核心问题:
1)在每一轮如何改变训练数据的权值或概率分布?
通过提高那些在前一轮被弱分类器分错样例的权值,减小前一轮分对样本的权值,而误分的样本在后续受到更多的关注.
2)通过什么方式来组合弱分类器?
通过加法模型将弱分类器进行线性组合,比如AdaBoost通过加权多数表决的方式,即增大错误率小的分类器的权值,同时减小错误率较大的分类器的权值.
而提升树通过拟合残差的方式逐步减小残差,将每一步生成的模型叠加得到最终模型.
3、Bagging,Boosting二者之间的区别
Bagging和Boosting的区别:
1)样本选择上:
Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的.
Boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化.而权值是根据上一轮的分类结果进行调整.
2)样例权重:
Bagging:使用均匀取样,每个样例的权重相等
Boosting:根据错误率不断调整样例的权值,错误率越大则权重越大.
3)预测函数:
Bagging:所有预测函数的权重相等.
Boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重.
4)并行计算:
Bagging:各个预测函数可以并行生成
Boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果.
5)偏差和方差:
bagging是减少variance,而boosting是减少bias
bias度量模型预测结果和真实结果的偏离程度,刻画模型算法本身的拟合能力
variance度量同样大小的训练集的变动导致的学习能力的变化,刻画数据的分布情况造成的影响
下面是将决策树与这些算法框架进行结合所得到的新的算法:
1)Bagging + 决策树 = 随机森林
2)AdaBoost + 决策树 = 提升树
3)Gradient Boosting + 决策树 = GBDT
决策树
常用的决策树算法有ID3,C4.5,CART三种。3种算法的模型构建思想都十分类似,只是采用了不同的指标。决策树模型的构建过程大致如下:
ID3,C4.5决策树的生成
输入:训练集D,特征集A,阈值eps 输出:决策树T
- 若D中所有样本属于同一类Ck,则T为单节点树,将类Ck作为该结点的类标记,返回T
- 若A为空集,即没有特征作为划分依据,则T为单节点树,并将D中实例数最大的类Ck作为该结点的类标记,返回T
- 否则,计算A中各特征对D的信息增益(ID3)/信息增益比(C4.5),选择信息增益最大的特征Ag
- 若Ag的信息增益(比)小于阈值eps,则置T为单节点树,并将D中实例数最大的类Ck作为该结点的类标记,返回T
- 否则,依照特征Ag将D划分为若干非空子集Di,将Di中实例数最大的类作为标记,构建子节点,由结点及其子节点构成树T,返回T
- 对第i个子节点,以Di为训练集,以A-{Ag}为特征集,递归地调用1~5,得到子树Ti,返回Ti
CART决策树的生成
这里只简单介绍下CART与ID3和C4.5的区别。
- CART树是二叉树,而ID3和C4.5可以是多叉树
- CART在生成子树时,是选择一个特征一个取值作为切分点,生成两个子树
- 选择特征和切分点的依据是基尼指数,选择基尼指数最小的特征及切分点生成子树
决策树的剪枝
决策树的剪枝主要是为了预防过拟合,过程就不详细介绍了。
主要思路是从叶节点向上回溯,尝试对某个节点进行剪枝,比较剪枝前后的决策树的损失函数值。最后我们通过动态规划(树形dp,acmer应该懂)就可以得到全局最优的剪枝方案。
4、随机森林
随机森林是Bagging的一个扩展变体,除了样本集是有放回的采样外,属性集合也引入了随机属性选择.具体来说,传统决策树在选择划分属性时是在当前结点的属性集合中选择一个最优属性;而在RF中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,然后再从这个子集中选择一个最优属性用于划分.
随机森林简单、容易实现、计算开销小.效果能使得最终集成的泛化性能可通过个体学习器之间差异度的增加而进一步提升.
随机森林的构建过程大致如下:
1.从原始训练集中使用Bootstraping方法随机有放回采样选出m个样本,共进行n_tree次采样,生成n_tree个训练集
每棵树的训练集都是不同的,而且里面包含重复的训练样本(理解这点很重要)。
1) 为什么要随机抽样训练集?
如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的,这样的话完全没有bagging的必要;
2) 为什么要有放回地抽样?
我理解的是这样的:如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是"有偏的",都是绝对"片面的"(当然这样说可能不对),也就是说每棵树训练出来都是有很大的差异的;而随机森林最后分类取决于多棵树(弱分类器)的投票表决,这种表决应该是"求同",因此使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的,这样无异于是"盲人摸象"。
2.对于n_tree个训练集,我们分别训练n_tree个决策树模型
3.对于单个决策树模型,假设每个样本的特征维度为M,指定一个常数m<
4.每棵树都一直这样分裂下去尽最大程度的生长,直到该节点的所有训练样例都属于同一类。并且没有剪枝过程。
5.将生成的多棵决策树组成随机森林。对于分类问题,按多棵树分类器投票决定最终分类结果;对于回归问题,由多棵树预测值的均值决定最终预测结果
随机森林中的“随机”就是指的这里的两个随机性。两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入,使得随机森林不容易陷入过拟合,并且具有很好得抗噪能力(比如:对缺省值不敏感)。
随机森林分类效果(错误率)与两个因素有关:
- 森林中任意两棵树的相关性:相关性越大,错误率越大;
- 森林中每棵树的分类能力:每棵树的分类能力越强,整个森林的错误率越低。
减小特征选择个数m,树的相关性和分类能力也会相应的降低;增大m,两者也会随之增大。所以关键问题是如何选择最优的m(或者是范围),这也是随机森林唯一的一个参数。
5.AdaBoost
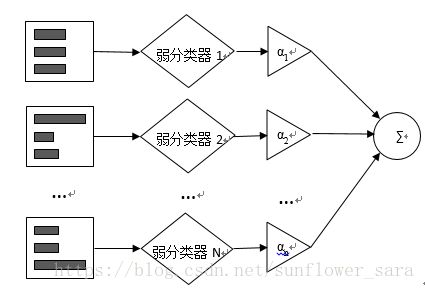
AdaBoost对于每个弱分类器的准确率要求并不高,即便是低于50%的随机实验的准确率水平也可以。最后通过对训练所得的弱分类器进行线性加权组合就可以得到一个强分类器。
加法模型就是说强分类器由一系列弱分类器线性相加而成。一般组合形式如下:
其中,![]() 就是一个个的弱分类器,am是弱分类器学习到的最优参数,βm就是弱学习在强分类器中所占比重,PP是所有am和βm的组合。这些弱分类器线性相加组成强分类器。
就是一个个的弱分类器,am是弱分类器学习到的最优参数,βm就是弱学习在强分类器中所占比重,PP是所有am和βm的组合。这些弱分类器线性相加组成强分类器。
前向分步就是说在训练过程中,下一轮迭代产生的分类器是在上一轮的基础上训练得来的。也就是可以写成这样的形式:
AdaBoost的运行过程如下:
先对数据集中的一部分样本训练。赋予这部分样本中的每一个样本一个相同的权重,并构成权重向量D。这些权重在一开始都被初始化赋予相等的值,如图4.2最左上方的正方体所示。
根据数据训练分类器,找根据这些权重算出来的误差最小的那个分类器作为这次的弱分类器
先在根据这部分训练数据训练出一个弱分类器。该弱分类器可以是任何一种分类器,但是最好是简单分类器,例如决策树等。得到第一个弱分类器后计算其错误率。其中,错误率ε的定义为:
为了最终实现对所有弱分类器进行整合的目的,AdaBoost为每个弱分类器都配备了一个权重值α。
根据此选出的弱分类器的错误率重写计算误差,更新分类器权重
得到第一个弱分类器的错误率之后,根据此错误率,计算第一个弱分类器的权重α。计算公式如下:
根据公式更新样本权重
之后,根据情况更新每个样本的权重,第一个弱分类器分类正确的样本权重会降低,分类错误的样本权重会升高,对权重向量D进行更新,更新方法如公式4.5以及4.6所示:
如果样本被正确分类,则权重变为:
而如果样本被错误分类,则权重变为:
(因为根据公式,错分类样本会让误差变大,然后在更新分类器权重的时候就会降低分错的分类器的权重;反之亦然)
当弱分类器权重α以及样本权重D都进行了更新之后,AdaBoost会重复以上训练过程进行新一轮弱分类器的训练等步骤,每次都会调整权重,直到训练错误率为0或者弱分类器的数目达到设定值为止,最终训练出多个弱分类器并得到相应的权重[24]。
为何AdaBoost一定要使用简单分类器?
当使用简单分类器时,计算出的结果是可以理解的
Adaboost算法优缺点:
优点
1) Adaboost是一种有很高精度的分类器
2) 可以使用各种方法构建子分类器,Adaboost算法提供的是框架
3) 当使用简单分类器时,计算出的结果是可以理解的。而且弱分类器构造极其简单
4) 简单,不用做特征筛选
5) 不用担心overfitting(过度拟合)
缺点
1) 容易受到噪声干扰,这也是大部分算法的缺点
2) 训练时间过长
3) 执行效果依赖于弱分类器的选择
超级推荐的博客参考资料,有一个例子的详细的计算过程
https://blog.csdn.net/guyuealian/article/details/70995333
6.GBDT梯度下降树
https://www.cnblogs.com/ModifyRong/p/7744987.html
-
- 但是其实我们真正关注的,1.是希望损失函数能够不断的减小,2.是希望损失函数能够尽可能快的减小。所以如何尽可能快的减小呢?
-
- 让损失函数沿着梯度方向的下降。这个就是gbdt 的 gb的核心了。 利用损失函数的负梯度在当前模型的值作为回归问题提升树算法中的残差的近似值去拟合一个回归树。gbdt 每轮迭代的时候,都去拟合损失函数在当前模型下的负梯度。
-
- 这样每轮训练的时候都能够让损失函数尽可能快的减小,尽快的收敛达到局部最优解或者全局最优解。
- gbdt如何选择特征?
gbdt选择特征的细节其实是想问你CART Tree生成的过程。这里有一个前提,gbdt的弱分类器默认选择的是CART TREE。其实也可以选择其他弱分类器的,选择的前提是低方差和高偏差。框架服从boosting 框架即可。
下面我们具体来说CART TREE(是一种二叉树) 如何生成。CART TREE 生成的过程其实就是一个选择特征的过程。假设我们目前总共有 M 个特征。第一步我们需要从中选择出一个特征 j,做为二叉树的第一个节点。然后对特征 j 的值选择一个切分点 m. 一个 样本的特征j的值 如果小于m,则分为一类,如果大于m,则分为另外一类。如此便构建了CART 树的一个节点。其他节点的生成过程和这个是一样的。现在的问题是在每轮迭代的时候,如何选择这个特征 j,以及如何选择特征 j 的切分点 m:
-
- 原始的gbdt的做法非常的暴力,首先遍历每个特征,然后对每个特征遍历它所有可能的切分点,找到最优特征 m 的最优切分点 j。
7.Xgboost
什么是 xgboost?
强推此文!!! http://blog.itpub.net/31542119/viewspace-2199549/
XGBoost :eXtreme Gradient Boosting
项目地址:https://github.com/dmlc/xgboost
是由 Tianqi Chen http://homes.cs.washington.edu/~tqchen/ 最初开发的实现可扩展,便携,分布式 gradient boosting (GBDT, GBRT or GBM) 算法的一个库,可以下载安装并应用于 C++,Python,R,Julia,Java,Scala,Hadoop,现在有很多协作者共同开发维护。
XGBoost 所应用的算法就是 gradient boosting decision tree,既可以用于分类也可以用于回归问题中。
https://www.cnblogs.com/dudumiaomiao/p/6361777.html
https://blog.csdn.net/qq547276542/article/details/78304454
http://www.cnblogs.com/maybe2030/p/4585705.html
https://www.cnblogs.com/ScorpioLu/p/8295990.html