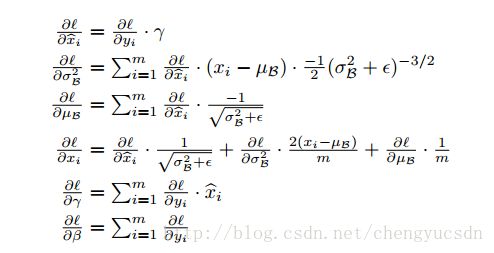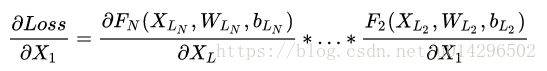避免过拟合的方法，正则化，dropout，Batch normalization

避免过拟合的方法，正则化，dropout，Batch normalization

目录

避免过拟合的方法，正则化，dropout，Batch normalization

一、铺垫

1.奥卡姆剃刀原则

2.简单模型上的过拟合

3.深度学习过拟合

4.数据集的划分与过拟合

二、防止过拟合的方法

1.添加噪声

2.early stopping

3.数据集扩增（Data augmentation）

4.数据均衡

5.正则化（Regularization）

（0）L1、L2总览

稀疏模型与特征选择

L1和L2正则化的直观理解

（1）L1正则化和特征选择

（2）L2正则化(权重衰减)和过拟合

（3）总结

6.Dropout

         7.Batch normalization

1）.为什么要用BN

①加速收敛

②防止过拟合

③降低网络对初始化权重敏感

④允许使用较大的学习率

2).训练中如何batchnormalization

3).BN层反向传播公式推导

4).测试（inference）时如何batchnormalization

8.不同的激活函数

9.残差结构

网络过深后果：

shortcut的思想：

10.LSTM

11.参考资料

---

一、铺垫

1.奥卡姆剃刀原则

根据奥卡姆剃刀原则，应该是模型越简单越好。

因为参数太多，会导致我们的模型复杂度上升，容易过拟合

 

2.简单模型上的过拟合

模型越复杂，越容易过拟合。

因此，原先以最小化损失（经验风险最小化）为目标：

现在以最小化损失和模型复杂度（结构风险最小化）为目标：

通过降低复杂模型的复杂度来防止过拟合的规则称为正则化。

3.深度学习过拟合

深度学习过程中，在训练数据不够多时，或者overtraining时，常常会导致overfitting（过拟合）。其直观的表现如下图所示，随着训练过程的进行，模型复杂度增加，在training data上的error渐渐减小，但是在验证集上的error却反而渐渐增大——因为训练出来的网络过拟合了训练集，对训练集外的数据却不work。

 

4.数据集的划分与过拟合

有一个概念需要先说明，在机器学习算法中，我们常常将原始数据集分为三部分：training data、validation data，testing data。这个validation data是什么？它其实就是用来避免过拟合的，在训练过程中，我们通常用它来确定一些超参数（比如根据validation data上的accuracy来确定early stopping的epoch大小、根据validation data确定learning rate等等）。那为啥不直接在testing data上做这些呢？因为如果在testing data做这些，那么随着训练的进行，我们的网络实际上就是在一点一点地overfitting我们的testing data，导致最后得到的testing accuracy没有任何参考意义。因此，training data的作用是计算梯度更新权重，validation data如上所述，testing data则给出一个accuracy以判断网络的好坏。

 

二、防止过拟合的方法

避免过拟合的方法有很多：添加噪声，early stopping、数据集扩增（Data augmentation）、数据均衡、正则化（Regularization）包括L1、L2（L2 regularization也叫weight decay），dropout。

1.添加噪声

数据原本有噪声，添加噪声可能可以抵消原本的噪声的影响

 

2.early stopping

观察loss的曲线变化情况，训练测试验证集曲线平滑后即可停止训练，否则可能导致test的曲线上升，发生过拟合

 

3.数据集扩增（Data augmentation）

通过改变图像的亮度，旋转，切分等操作，增大数据集样本量

 

“有时候不是因为算法好赢了，而是因为拥有更多的数据才赢了。”

不记得原话是哪位大牛说的了，hinton？从中可见训练数据有多么重要，特别是在深度学习方法中，更多的训练数据，意味着可以用更深的网络，训练出更好的模型。

既然这样，收集更多的数据不就行啦？如果能够收集更多可以用的数据，当然好。但是很多时候，收集更多的数据意味着需要耗费更多的人力物力，有弄过人工标注的同学就知道，效率特别低，简直是粗活。

所以，可以在原始数据上做些改动，得到更多的数据，以图片数据集举例，可以做各种变换，如：

• 将原始图片旋转一个小角度

• 添加随机噪声

• 一些有弹性的畸变（elastic distortions），论文《Best practices for convolutional neural networks applied to visual document analysis》对MNIST做了各种变种扩增。

• 截取（crop）原始图片的一部分。比如DeepID中，从一副人脸图中，截取出了100个小patch作为训练数据，极大地增加了数据集。感兴趣的可以看《Deep learning face representation from predicting 10,000 classes》.

  更多数据意味着什么？

用50000个MNIST的样本训练SVM得出的accuracy94.48%，用5000个MNIST的样本训练NN得出accuracy为93.24%，所以更多的数据可以使算法表现得更好。在机器学习中，算法本身并不能决出胜负，不能武断地说这些算法谁优谁劣，因为数据对算法性能的影响很大。

 

 

4.数据均衡

negative和positive的数据量要基本保持1：1的比例。

可以通过数据集过充的过程达到这个效果。

但是样本数量一样多并不意味着样本完全均衡，样本总有容易区分的和不容易区分的，分布不均衡。可以通过改变lost fucntion，不使用交叉熵，比如使用focal loss，来解决这个问题。

 

5.正则化（Regularization）

（0）L1、L2总览

机器学习中几乎都可以看到损失函数后面会添加一个额外项，常用的额外项一般有两种，一般英文称作ℓ1ℓ1-norm和ℓ2ℓ2-norm，中文称作L1正则化和L2正则化，或者L1范数和L2范数。

L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。

 

下图是Python中Lasso回归的损失函数，式中加号后面一项α||w||1α||w||1即为L1正则化项。

下图是Python中Ridge回归的损失函数，式中加号后面一项α||w||22α||w||22即为L2正则化项。

一般回归分析中回归ww表示特征的系数，从上式可以看到正则化项是对系数做了处理（限制）。

L1正则化和L2正则化的说明如下：

• L1正则化是指权值向量ww中各个元素的绝对值之和，通常表示为||w||1||w||1
• L2正则化是指权值向量ww中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为||w||2||w||2

 

一般都会在正则化项之前添加一个系数，Python中用αα表示，一些文章也用λλ表示。这个系数需要用户指定。

 

那添加L1和L2正则化有什么用？

下面是L1正则化和L2正则化的作用，这些表述可以在很多文章中找到。

• L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
• L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合

稀疏模型与特征选择

上面提到L1正则化有助于生成一个稀疏权值矩阵，进而可以用于特征选择。为什么要生成一个稀疏矩阵？

稀疏矩阵指的是很多元素为0，只有少数元素是非零值的矩阵，即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，或者贡献微小（因为它们前面的系数是0或者是很小的值，即使去掉对模型也没有什么影响），此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。

L1和L2正则化的直观理解

这部分内容将解释为什么L1正则化可以产生稀疏模型（L1是怎么让系数等于零的），以及为什么L2正则化可以防止过拟合。

（1）L1正则化和特征选择

假设有如下带L1正则化的损失函数： 

J=J0+α∑w|w|(1)(1)J=J0+α∑w|w|

其中J0J0是原始的损失函数，加号后面的一项是L1正则化项，αα是正则化系数。注意到L1正则化是权值的绝对值之和，JJ是带有绝对值符号的函数，因此JJ是不完全可微的。机器学习的任务就是要通过一些方法（比如梯度下降）求出损失函数的最小值。当我们在原始损失函数J0J0后添加L1正则化项时，相当于对J0J0做了一个约束。令L=α∑w|w|L=α∑w|w|，则J=J0+LJ=J0+L，此时我们的任务变成在LL约束下求出J0J0取最小值的解。考虑二维的情况，即只有两个权值w1w1和w2w2，此时L=|w1|+|w2|L=|w1|+|w2|对于梯度下降法，求解J0J0的过程可以画出等值线，同时L1正则化的函数LL也可以在w1w2w1w2的二维平面上画出来。如下图：

 

 
图1 L1正则化

图中等值线是J0J0的等值线，黑色方形是LL函数的图形。在图中，当J0J0等值线与LL图形首次相交的地方就是最优解。上图中J0J0与LL在LL的一个顶点处相交，这个顶点就是最优解。注意到这个顶点的值是(w1,w2)=(0,w)(w1,w2)=(0,w)。可以直观想象，因为LL函数有很多『突出的角』（二维情况下四个，多维情况下更多），J0J0与这些角接触的机率会远大于与LL其它部位接触的机率，而在这些角上，会有很多权值等于0，这就是为什么L1正则化可以产生稀疏模型，进而可以用于特征选择。

而正则化前面的系数αα，可以控制LL图形的大小。αα越小，LL的图形越大（上图中的黑色方框）；αα越大，LL的图形就越小，可以小到黑色方框只超出原点范围一点点，这是最优点的值(w1,w2)=(0,w)(w1,w2)=(0,w)中的ww可以取到很小的值。

类似，假设有如下带L2正则化的损失函数： 

J=J0+α∑ww2(2)(2)J=J0+α∑ww2

同样可以画出他们在二维平面上的图形，如下：

 

 
图2 L2正则化

二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此J0J0与LL相交时使得w1w1或w2w2等于零的机率小了许多，这就是为什么L2正则化不具有稀疏性的原因。

 

在原始的代价函数后面加上一个L1正则化项，即所有权重w的绝对值的和，乘以λ/n（这里不像L2正则化项那样，需要再乘以1/2）

同样先计算导数：

上式中sgn(w)表示w的符号。那么权重w的更新规则为：

比原始的更新规则多出了η * λ * sgn(w)/n这一项。

当w为正时，更新后的w变小。当w为负时，更新后的w变大——因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。

另外，上面没有提到一个问题，当w为0时怎么办？当w等于0时，|W|是不可导的，所以我们只能按照原始的未经正则化的方法去更新w，这就相当于去掉η*λ*sgn(w)/n这一项，所以我们可以规定sgn(0)=0，这样就把w=0的情况也统一进来了。（在编程的时候，令sgn(0)=0,sgn(w>0)=1,sgn(w<0)=-1）

 

（2）L2正则化(权重衰减)和过拟合

拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是『抗扰动能力强』。

那为什么L2正则化可以获得值很小的参数？

以线性回归中的梯度下降法为例。假设要求的参数为θθ，hθ(x)hθ(x)是我们的假设函数，那么线性回归的代价函数如下： 

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2(3)(3)J(θ)=12m∑i=1m(hθ(x(i))−y(i))2

那么在梯度下降法中，最终用于迭代计算参数θθ的迭代式为： 

θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))x(i)j(4)(4)θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))xj(i)

其中αα是learning rate. 上式是没有添加L2正则化项的迭代公式，如果在原始代价函数之后添加L2正则化，则迭代公式会变成下面的样子： 

θj:=θj(1−αλm)−α1m∑i=1m(hθ(x(i))−y(i))x(i)j(5)(5)θj:=θj(1−αλm)−α1m∑i=1m(hθ(x(i))−y(i))xj(i)

其中λλ就是正则化参数。从上式可以看到，与未添加L2正则化的迭代公式相比，每一次迭代，θjθj都要先乘以一个小于1的因子，从而使得θjθj不断减小，因此总得来看，θθ是不断减小的。

 

最开始也提到L1正则化一定程度上也可以防止过拟合。之前做了解释，当L1的正则化系数很小时，得到的最优解会很小，可以达到和L2正则化类似的效果。

 

L2正则化就是在代价函数后面再加上一个正则化项：

C0代表原始的代价函数，后面那一项就是L2正则化项，它是这样来的：所有参数w的平方的和，除以训练集的样本大小n。λ就是正则项系数，权衡正则项与C0项的比重。另外还有一个系数1/2，1/2经常会看到，主要是为了后面求导的结果方便，后面那一项求导会产生一个2，与1/2相乘刚好凑整。

L2正则化项是怎么避免overfitting的呢？我们推导一下看看，先求导：

可以发现L2正则化项对b的更新没有影响，但是对于w的更新有影响:

在不使用L2正则化时，求导结果中w前系数为1，现在w前面系数为 1−ηλ/n ，因为η、λ、n都是正的，所以 1−ηλ/n小于1，它的效果是减小w，这也就是权重衰减（weight decay）的由来。当然考虑到后面的导数项，w最终的值可能增大也可能减小。

另外，需要提一下，对于基于mini-batch的随机梯度下降，w和b更新的公式跟上面给出的有点不同：

对比上面w的更新公式，可以发现后面那一项变了，变成所有导数加和，乘以η再除以m，m是一个mini-batch中样本的个数。

 

L2正则化项有让w“变小”的效果，但是还没解释为什么w“变小”可以防止overfitting？一个所谓“显而易见”的解释就是：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好（这个法则也叫做奥卡姆剃刀），而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果。

 

过拟合的时候，拟合函数的系数往往非常大，为什么？如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。

而正则化是通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。

（3）总结

1）. L1和L2的定义

L1正则化，又叫Lasso Regression

如下图所示，L1是向量各元素的绝对值之和

 

L2正则化，又叫Ridge Regression

如下图所示，L2是向量各元素的平方和

 

2）. L1和L2的异同点

相同点：都用于避免过拟合

不同点：L1可以让一部分特征的系数缩小到0，从而间接实现特征选择。所以L1适用于特征之间有关联的情况。

              L2让所有特征的系数都缩小，但是不会减为0，它会使优化求解稳定快速。所以L2适用于特征之间没有关联的情况

 

3）.L1和L2的结合

L1和L2的优点可以结合起来，这就是Elastic Net

 

6.Dropout

L1、L2正则化是通过修改代价函数来实现的，而Dropout则是通过修改神经网络本身来实现的，它是在训练网络时用的一种技巧（trike）。它的流程如下：

假设我们要训练上图这个网络，在训练开始时，我们随机地“删除”一半的隐层单元，视它们为不存在，得到如下的网络：

保持输入输出层不变，按照BP算法更新上图神经网络中的权值（虚线连接的单元不更新，因为它们被“临时删除”了）。

以上就是一次迭代的过程，在第二次迭代中，也用同样的方法，只不过这次删除的那一半隐层单元，跟上一次删除掉的肯定是不一样的，因为我们每一次迭代都是“随机”地去删掉一半。第三次、第四次……都是这样，直至训练结束。

以上就是Dropout，它为什么有助于防止过拟合呢？可以简单地这样解释，运用了dropout的训练过程，相当于训练了很多个只有半数隐层单元的神经网络（后面简称为“半数网络”），每一个这样的半数网络，都可以给出一个分类结果，这些结果有的是正确的，有的是错误的。随着训练的进行，大部分半数网络都可以给出正确的分类结果，那么少数的错误分类结果就不会对最终结果造成大的影响。

更加深入地理解，可以看看Hinton和Alex两牛2012的论文《ImageNet Classification with Deep Convolutional Neural Networks》

 

 

例子

from __future__ import print_function
import tensorflow as tf
from sklearn.datasets import load_digits
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import LabelBinarizer
 
# load data
digits = load_digits()
X = digits.data
y = digits.target
y = LabelBinarizer().fit_transform(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3)
 
 
def add_layer(inputs, in_size, out_size, layer_name, activation_function=None, ):
    # add one more layer and return the output of this layer
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1, )
    Wx_plus_b = tf.matmul(inputs, Weights) + biases
    # here to dropout
    Wx_plus_b = tf.nn.dropout(Wx_plus_b, keep_prob)
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b, )
    tf.histogram_summary(layer_name + '/outputs', outputs)
    return outputs
 
 
# define placeholder for inputs to network
keep_prob = tf.placeholder(tf.float32)
xs = tf.placeholder(tf.float32, [None, 64])  # 8x8
ys = tf.placeholder(tf.float32, [None, 10])
 
# add output layer
l1 = add_layer(xs, 64, 50, 'l1', activation_function=tf.nn.tanh)
prediction = add_layer(l1, 50, 10, 'l2', activation_function=tf.nn.softmax)
 
# the loss between prediction and real data
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf.log(prediction),
                                              reduction_indices=[1]))  # loss
tf.scalar_summary('loss', cross_entropy)
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
 
sess = tf.Session()
merged = tf.merge_all_summaries()
# summary writer goes in here
train_writer = tf.train.SummaryWriter("logs/train", sess.graph)
test_writer = tf.train.SummaryWriter("logs/test", sess.graph)
 
sess.run(tf.initialize_all_variables())
 
for i in range(500):
    # here to determine the keeping probability
    sess.run(train_step, feed_dict={xs: X_train, ys: y_train, keep_prob: 0.5})
    if i % 50 == 0:
        # record loss
        train_result = sess.run(merged, feed_dict={xs: X_train, ys: y_train, keep_prob: 1})
        test_result = sess.run(merged, feed_dict={xs: X_test, ys: y_test, keep_prob: 1})
        train_writer.add_summary(train_result, i)
        test_writer.add_summary(test_result, i)

1）训练的时候dropout，验证和测试的时候不dropout

sess.run(train_step, feed_dict={xs: X_train, ys: y_train, keep_prob: 0.5})
train_result = sess.run(merged, feed_dict={xs: X_train, ys: y_train, keep_prob: 1})
test_result = sess.run(merged, feed_dict={xs: X_test, ys: y_test, keep_prob: 1})

2）dropout必须设置概率keep_prob,并且keep_prob也是一个占位符,跟输入是一样的

训练时设置keep_prob≠1 （一般0.4-0.6之间，数据量少了就取大点），验证和测试时=1

keep_prob = tf.placeholder(tf.float32)

3）tf实现dropout其实,就一个函数,让一个神经元以某一固定的概率失活

def add_layer(inputs, in_size, out_size, layer_name, activation_function=None, ):
    # add one more layer and return the output of this layer
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1, )
    Wx_plus_b = tf.matmul(inputs, Weights) + biases
    # here to dropout
    Wx_plus_b = tf.nn.dropout(Wx_plus_b, keep_prob)
    return Wx_plus_b 

 

实现:

参考博客 https://blog.csdn.net/lujiandong1/article/details/53223630/

 

7.Batch normalization

1）.为什么要用BN

BN（Batch Normalization）层的作用总结

1. 加速收敛
2. 控制过拟合，可以少用或不用Dropout和正则
3. 降低网络对初始化权重敏感
4. 允许使用较大的学习率

 

①加速收敛

数据本身在0均值处

A.输入的分布

 在神经网络训练过程中，经常会出现梯度爆炸或者梯度消失的问题，导致网络训练困难，特别是在网络层数较多的情况下，网络层数多，网络更新一次，较后的层的输入数据的分布会发生较大变化，所以后面的层又要适应这种变化，相当于要求这些层能适应不同分布的输入，并总结出规律，这就导致网络训练很慢，而且不一定会收敛。如果保证每一层的输入的分布是稳定的，那么网络训练起来会收敛的更快，而且更不依赖于初始化的值。

统计机器学习中的一个经典假设是“源空间（source domain）和目标空间（target domain）的数据分布（distribution）是一致的”。如果不一致，那么就出现了新的机器学习问题，如，transfer learning/domain adaptation等。

因此至少0均值1方差的数据集可以减少样本分布的变化问题

B.均值为0，方差为1的高斯分布

先前的研究中表明，对数据做白化之后可以加快网络的收敛，受此启发，作者想到在训练的时候，可以对每一层的输入数据做白化，白化就是通过空间变换把数据变成均值为0，方差为1的高斯分布，然而白化操作是很复杂费时。退而求其次，将白化改成将输入做移动和线性变换，使得输入的均值为0，方差为1。

 

C.系数r,和偏置b

 单纯的归一化之后，数据的分布为均值为0，方差为1，BN层的输出就很有可能在在激活函数的线性段，多个线性层可以用一个线性来代替，这样网络的非线性表达能力就不好，所以加上一个系数r,和偏置b，让输入能够到达激活函数的非线性区域，这两个参数可以让网络自学习。尤其是当两个参数如下时，输入为原始输入。这样输入既可以是原始输入也可以是归一化后的输入，也可以是归一化后的输入的线性变换，让网络自己学习要什么样的输入。

 

②防止过拟合

可以少用或不用Dropout和正则

使用BN训练时，一个样本只与minibatch中其他样本有相互关系；对于同一个训练样本，网络的输出会发生变化。这些效果有助于提升网络泛化能力，像dropout一样防止网络过拟合，同时BN的使用，可以减少或者去掉dropout类似的策略。

③降低网络对初始化权重敏感

初始化的时候，我们的参数一般都是0均值的，因此开始的拟合y=Wx+b，基本过原点附近，如图b红色虚线。因此，网络需要经过多次学习才能逐步达到如紫色实线的拟合，即收敛的比较慢。如果我们对输入数据先作减均值操作，如图c，显然可以加快学习。更进一步的，我们对数据再进行去相关操作，使得数据更加容易区分，这样又会加快训练，如图d。 通过把梯度映射到一个值大但次优的变化位置来阻止梯度过小变化。

④允许使用较大的学习率

在每一层输入的时候，加个BN预处理操作。BN应作用在非线性映射前，即对x=Wu+b做规范化。在BN中，是通过将activation规范为均值和方差一致的手段使得原本会减小的activation的scale变大。可以说是一种更有效的local response normalization方法

 

2).训练中如何batchnormalization

BN层执行的操作如下图，eps的作用是保证分母不会除零，计算每个featuremap的minibatch集内的均值方差，归一化每个神经元xi，也就是CNN中featuremap的每个像素点，然后乘一个系数r，加上偏置b(初始化时一般r=1,b=0)，得到输出yi，然后yi输入到激活函数，激活函数的输出再输入下一个卷积层，下一个卷积层的输出又重复以上操作。一般BN层都加在非线性层前面。参数r,b也是通过反向传播算法学习得到。所以在训练中，forward和backward都经过BN层。

   梯度反向传播计算公式（epsilon用来防止除0）

3).BN层反向传播公式推导

http://blog.csdn.net/pan5431333/article/details/78052867

4).测试（inference）时如何batchnormalization

 在训练时，归一化输入用的是minibatch的均值方差，而实际上，整个训练集的均值方差是最能反映数据分布的，但是由于训练的计算量考虑，用随机抽取的minibatch也能大致反映数据的分布。但是到了测试的时候，输入只有一个，BN无法对一个输入归一化，所以在网络每次训练时，会保存每个minibatch的均值方差，在网络训练好之后，BN层的均值方差用之前训练用的所有minibatch对整个数据集的均值方差的无偏估计量来代替。r,b任然用仍然用训练得到的参数。

8.不同的激活函数

relu 

Leaky ReLU 

maxout

等激活函数

 

参考本博客另一篇博文

https://blog.csdn.net/sunflower_sara/article/details/81229352

9.残差结构

网络过深后果：

优：特征抽象

缺：信息损失 +  梯度损失或爆炸

 

shortcut的思想：

去掉主体，突出微小变化

对输出变化更敏感

 

 

深度残差网络是ImageNet比赛中，效果最好的网络，残差网络的出现导致了image net比赛的终结，自从残差提出后，几乎所有的深度网络都离不开残差的身影，相比较之前的几层，几十层的深度网络，在残差网络面前都不值一提，残差可以很轻松的构建几百层，一千多层的网络而不用担心梯度消失过快的问题，原因就在于残差的捷径（shortcut）部分，其中

残差单元如下图所示： 
 
相比较于以前网络的直来直去结构，残差中有很多这样的跨层连接结构，这样的结构在反向传播中具有很大的好处，见下式： 
 
式子的第一个因子 ∂loss∂xL∂loss∂xL 表示的损失函数到达 L 的梯度，小括号中的1表明短路机制可以无损地传播梯度，而另外一项残差梯度则需要经过带有weights的层，梯度不是直接传递过来的。残差梯度不会那么巧全为-1，而且就算其比较小，有1的存在也不会导致梯度消失。所以残差学习会更容易。

注：上面的推导并不是严格的证明。

 

在深度学习的探究过程中，发现对深度的扩展远远比广度的扩展效果要达到的好的太多。理论认为，同层的不同神经元学习不同的特征，越往后层的神经元学习特征的抽象程度越高。可以这样理解，如果要识别一个汽车如下图：

上面的图我画的有些粗糙，但是意思应该表达清楚了，特征的组合识别一个物体，如果特征越抽象则识别物体更加简单，也就是说网络模型越深越好了？那么在搭建一个网络模型只要不停的加深网络不就能够得到更好的分类精度吗？

其实不然，随着网络层级的不断增加，模型精度不断得到提升，而当网络层级增加到一定的数目以后，训练精度和测试精度迅速下降，这说明当网络变得很深以后，深度网络就变得更加难以训练了。在不断加神经网络的深度时，模型准确率会先上升然后达到饱和，再持续增加深度时则会导致准确率下降。

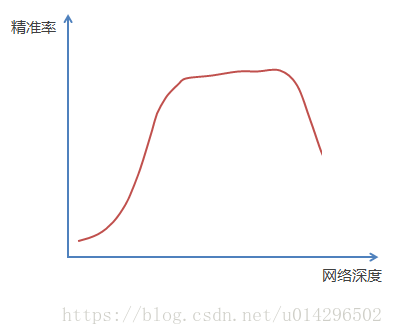
观察精准度的走势，随着网络层加深，精准度先是达到一个峰值，然后持续走低。误差是普遍存在的，无论是训练集还是验证集，随着误差的传播，越往后误差越大，所以越深的网络效果可能并不会很好。

解释一：按照信息熵的传播原理，信息在传播的过程中是有损失的，所以越深的网络能够学到的信息就越少，所以就更难训练。

解释二：另一个比较严谨的解释，因为神经网络在求梯度的时候有个链式法则，求解梯度时会有累乘造成了梯度弥散或者爆炸。

所以越深的网络越难训练，且效果可能会变差。

有什么办法可以寻找到一个最佳深度网络模型呢？如果我持续加深那么误差会变大，影响模型效果，并且也不清楚到底加多少层才是最佳。有没有一种方式，我可以持续加深网络？即使模型精确度已经饱和，我持续加深也不会对模型精准度有影响？答案是有的，这个时候引出ResNet网络，它是这样的，假设现有一个比较浅的网络（Shallow Net）已达到了饱和的准确率，这时在它后面再加上几个恒等映射层（Identity mapping，也即y=x，输出等于输入），这样就增加了网络的深度，并且起码误差不会增加，也即更深的网络不应该带来训练集上误差的上升。通过“shortcut connections（捷径连接）”的方式，直接把输入x传到输出作为初始结果，输出结果为H(x)=F(x)+x，当F(x)=0时，那么H(x)=x，也就是上面所提到的恒等映射。于是，ResNet相当于将学习目标改变了，不再是学习一个完整的输出，而是目标值H(X)和x的差值，也就是所谓的残差F(x) = H(x)-x，因此，后面的训练目标就是要将残差结果逼近于0，使到随着网络加深，准确率不下降。

也就是说，即使我并不知道多少层是最佳，我通过残差模块，即使已经错过最佳深度我至少模型的精度不会有影响。起初看到这种网络模型很是奇怪，如果是一个浅层网络就能达到饱和，那么后面的残差结构目标是学习一个恒等映射，那么学习目标为F(x)接近为0。既然这样，为什么要去学习这个映射？直接写个恒等函数，或者直接设置F(x)=0 输出为x不就行了？残差网络的目的是学到y=x恒等映射函数，那么不就相当于加上的残差网络在最后没起到作用吗？那么为什么会有效呢？
首先这个饱和的浅层网络本身就不好寻找，有可能在达到饱和浅层网络深度之前，由于误差的原因模型精度已经下降。那么为什么持续增加层，让模型学习一个恒等映射就会使得模型表达变好呢？

假设：如果不使用残差网络结构，这一层的输出F'(5)=5.1 期望输出 H(5)=5 ,如果想要学习H函数，使得F'(5)=H(5)=5,这个变化率较低，学习起来是比较困难的。但是如果设计为H(5)=F(5)+5=5.1，进行一种拆分，使得F(5)=0.1，那么学习目标是不是变为F(5)=0，一个映射函数学习使得它输出由0.1变为0，这个是比较简单的。也就是说引入残差后的映射对输出变化更敏感了。

进一步理解：如果F'(5)=5.1 ,现在继续训练模型，使得映射函数F'(5)=5。(5.1-5)/5.1=2%，也许你脑中已经闪现把学习率从0.01设置为0.0000001。浅层还好用，深层的话可能就不太好使了。如果设计为残差结构呢？5.1变化为5，也就是F(5)=0.1变化为F(5)=0.这个变化率增加了100%。引入残差后映射对输出变化变的更加敏感了，这也就是为什么ResNet虽然层数很多但是收敛速度也不会低的原因。明显后者输出变化对权重的调整作用更大，所以效果更好。

残差的思想都是去掉相同的主体部分，从而突出微小的变化，看到残差网络我第一反应就是差分放大器。这也就是当网络模型我们已经设计到一定的深度，出现了精准度下降，如果使用残差结构就会很容易的调节到一个更好的效果，即使你不知道此刻的深度是不是最佳，但是起码准确度不会下降。代码实现也比较简单，原本的输出结果由F(x)替换为输出F(x)+X，如果维度相同则直接相加，如果维度不同则利用1*1的卷积核变换。当然残差网络还有很多细节， 比如使用预batch normalize ,ResNet-v1 由relu非线性变换，替换为ResNet-v2恒等变换。

 

可以参考

 https://blog.csdn.net/u014296502/article/details/80438616

说起残差的话，不得不提这篇论文了：Deep Residual Learning for Image Recognition，关于这篇论文的解读，可以参考知乎链接：https://zhuanlan.zhihu.com/p/31852747这里只简单介绍残差如何解决梯度的问题。 

 

10.LSTM

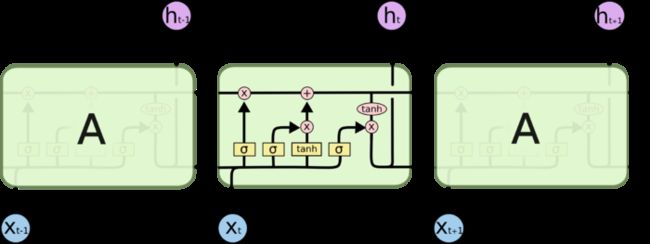
LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)，如下图，LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“，因此，经常用于生成文本中。目前也有基于CNN的LSTM，感兴趣的可以尝试一下。

 

LSTM用加和的方式取代了RNN的乘积，使得很难出现梯度弥散。但是相应的更大的几率会出现梯度爆炸，但是可以通过给梯度加门限解决这一问题。 

 

11.参考资料

编辑加总结以下资料

https://baijiahao.baidu.com/s?id=1595711904189222402&wfr=spider&for=pc

https://blog.csdn.net/jinlong_xu/article/details/77886731

https://blog.csdn.net/jinping_shi/article/details/52433975

https://hit-scir.gitbooks.io/neural-networks-and-deep-learning-zh_cn/content/chap3/c3s5ss2.html

https://blog.csdn.net/u012162613/article/details/44261657

https://blog.csdn.net/zouxy09/article/details/24971995

https://blog.csdn.net/chengyucsdn/article/details/79144107

https://www.cnblogs.com/pigbreeder/p/8051442.html

https://blog.csdn.net/qq_25737169/article/details/78847691