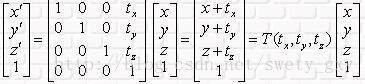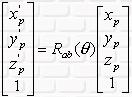三维空间中的几何变换-平移旋转缩放
前言
前段时间由于项目需要，深入学习了下图形几何变换，主要是绕任意轴旋转部分（其他的已有一定基础），现记录学习笔记。
文章内容部分引用并参考了下面的博客：
http://netclass.csu.edu.cn/NCourse/hep089/Chapter6/CG_Txt_6_012.htm
http://www.cnblogs.com/graphics/archive/2012/08/10/2627458.html
原理
由于用齐次坐标表示，三维几何变换的矩阵是一个4阶方阵，其形式如下：
。
其中，
产生按轴缩放、旋转、错切等变换。
产生平移变换，
产生投影变换，
产生整体的缩放变换。
（1）平移
三维平移变换的计算，通常是左乘一个平移矩阵，表示方式可以如下：
。
（2）缩放
对于空间任意参考点
的缩放变换，缩放矩阵的形成过程如下：
<1>将参考点平移到原点处；
<2>进行缩放变换；
<3>平移回原位置；
则最终变换矩阵结果如下：
，
其中，等号左边中间的矩阵的由缩放矢量（分别对应x轴、y轴，z轴方向的缩放）构成的缩放矩阵。
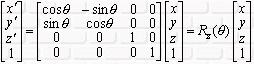
（3）绕坐标轴旋转
考虑右手坐标系下相对坐标原点绕坐标轴旋转q 角的变换：
<1>绕X轴转
<2>绕Y轴转
<3>绕Z轴转
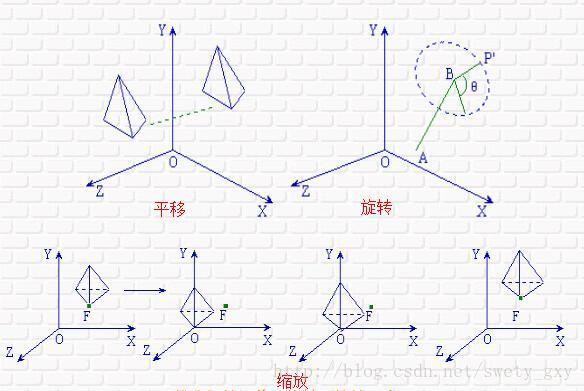
三维空间的平移旋转及缩放的示意图可如下表示：
（4）绕任意轴旋转
设旋转轴AB由任意一点A（xa，ya，za）及其方向数(a，b，c)定义，
可以通过下列步骤来实现P点的旋转：
A. 将A点移到坐标原点。
B. 使AB分别绕X轴、Y轴旋转适当角度与Z轴重合。
D.作上述变换的逆操作，使AB回到原来位置。
是AB在YOZ平面与XOZ平面的投影与Z轴的夹角。
我们可以得到如下的矩阵：
设旋转轴A(a,b,c)过原点，旋转角度为θ，
则旋转矩阵为：
设旋转轴A(u,v,w)不过原点，P(a,b,c)是旋转轴的起点，旋转角度为θ，
则旋转矩阵为：
对一个三维顶点作任意轴的旋转变换，只需左乘旋转矩阵即可。
示例代码
<1>空间点绕任意旋转轴旋转，函数输入参数是单位化后的轴方向、轴上任一点、旋转角度、要旋转的点
void RotateVecPoint(float& angle, osg::Vec3& N, osg::Vec3 center, osg::Vec3& Pt)
{
//输入参数是旋转轴上的任意一点P(a,b,c)，单位化后的旋转轴方向向量N(u,v,w），旋转角度θ,要旋转的点
float mcos = cos(angle), msin = sin(angle);
/*若旋转轴过原点*/
/*osg::Matrixf mat = osg::Matrixf(
pow(N.x(), 2)*(1 - mcos) + mcos, N.x()*N.y()*(1 - mcos) + N.z()*msin, N.x()*N.z()*(1 - mcos) - N.y()*msin, 0.0,
N.x()*N.y()*(1 - mcos) - N.z()*msin, pow(N.y(), 2)*(1 - mcos) + mcos, N.y()*N.z()*(1 - mcos) + N.x()*msin, 0.0,
N.x()*N.z()*(1 - mcos) + N.y()*msin, N.y()*N.z()*(1 - mcos) - N.x()*msin, pow(N.z(), 2)*(1 - mcos) + mcos, 0.0,
0.0, 0.0, 0.0, 1.0);*/
/*若旋转轴不过原点:涵盖了上面的情况*/
float a = center.x(), b = center.y(), c = center.z();//轴所在直线起点
float u = N.x(), v = N.y(), w = N.z();
//转置
osg::Matrixf mat = osg::Matrixf(
u*u + (v*v + w*w)*mcos, v*u*(1 - mcos) + w*msin, w*u*(1 - mcos) - v*msin, 0.0,
u*v*(1 - mcos) - w*msin, v*v + (u*u + w*w)*mcos, v*w*(1 - mcos) + u*msin, 0.0,
u*w*(1 - mcos) + v*msin, v*w*(1 - mcos) - u*msin, w*w + (u*u + v*v)*mcos, 0.0,
(a*(v*v + w*w) - u*(b*v + c*w))*(1 - mcos) + (b*w - c*v)*msin, (b*(u*u + w*w) - v*(a*u + c*w))*(1 - mcos) + (c*u - a*w)*msin, (c*(u*u + v*v) - w*(a*u + b*v))*(1 - mcos) + (a*v - b*u)*msin, 1.0
);
mat.preMult(Pt);
}效果图
<1>空间圆绕着任意轴旋转一定的角度
关于几何变换更详细的描述请参考：
http://netclass.csu.edu.cn/NCourse/hep089/Chapter6/CG_Txt_6_012.htm
http://www.cnblogs.com/graphics/archive/2012/08/10/2627458.html