最小二乘法与梯度下降法、牛顿法、高斯-牛顿法的理解
最小二乘法与梯度下降法、牛顿法、高斯-牛顿法的理解
最小二乘法
我们知道,当我们解 n n n元线性方程组时,如果有恰好有 n n n个方程(假设线性无关),那么可以得出对应的唯一解;二档方程个数大于 n n n时,如何确定未知数的值呢?
再举一个更具体的例子:
例如我们收集到了 N N N组有关立定跳远成绩( y y y)和身高( x x x)的数据 { ( x i , y j ) ∣ i = 1 , 2 , ⋯ , N } \{ (x_i,y_j)| i=1,2,\cdots, N \} {(xi,yj)∣i=1,2,⋯,N},并希望探寻二者之间的关系关系。假设通过画散点图我们看出二者之间呈线性关系,因而用 y = a x + b y = ax+b y=ax+b的线性模型进行回归。这本质上也是一个解方程的问题,方程的个数,即数据量(一般)远大于变量个数(2)。我们显然不能直接取其中两点并连线作为拟合曲线,这样的话其余的数据的价值完全没有体现出来,且这样拟合的结果很可能与数据整体呈现的分布趋势大相径庭。而**最小二乘法(Least Square Method,LSM)**就可以实现这种数据分布“整体衡量”或称“全局最优”的拟合。
最小二乘法的核心思想是计算误差函数(Loss Function)
ε = ∑ i = 1 N ( y ^ i − y i ) 2 = ∑ i = 1 N ( a x i + b − y i ) 2 (1.1) \varepsilon = \sum_{i=1}^N \left( \hat y_i-y_i \right)^2 = \sum_{i=1}^N \left( ax_i+b-y_i \right)^2 \tag{1.1} ε=i=1∑N(y^i−yi)2=i=1∑N(axi+b−yi)2(1.1)
并令其最小,此时对应的参数 a , b a,b a,b即为所求。
求解时,可以分别对 a , b a,b a,b求偏导再求零点,从而求得最佳匹配的 a , b a,b a,b:
{ ∂ ε ∂ a = 2 ∑ i = 1 N ( a x i + b − y i ) x i = 0 ∂ ε ∂ b = 2 ∑ i = 1 N ( a x i + b − y i ) = 0 (1.2) \begin{cases} \dfrac{\partial \varepsilon}{\partial a} = 2\sum_{i=1}^N \left( ax_i+b-y_i \right)x_i = 0\\ \dfrac{\partial \varepsilon}{\partial b} = 2\sum_{i=1}^N \left( ax_i+b-y_i \right) = 0 \end{cases} \tag{1.2} ⎩⎪⎨⎪⎧∂a∂ε=2∑i=1N(axi+b−yi)xi=0∂b∂ε=2∑i=1N(axi+b−yi)=0(1.2)
对于线性情况,我们可以将对应关系写为矩阵形式 A x ⃗ = b ⃗ \bold A \vec x = \vec b Ax=b,并得出闭合的解析解
( A T A ) − 1 A T b ⃗ (1.3) \left(\bold A^{\rm T}\bold A\right)^{-1}\bold A^{\rm T} \vec b \tag{1.3} (ATA)−1ATb(1.3)
对应的MATLAB命令为x = A\b。
实际上,除此之外,对于最小化式 ( 1.1 ) (1.1) (1.1)的方法,还有多种,下面尽量以通俗简明的方式,介绍其中三种的基本原理。
梯度下降法
上面的例子中,只有两个未知数,尚且可以使用偏导数置零的方法求解;但当未知数增加时,计算量将会快速增加。此外,LSM只对线性情况有解析解,非线性情况无法求解。在这时我们可以使用梯度下降法(Gradient Descent Method)。其本质是一种迭代求解目标函数最小值的方法,应用在LSM的问题中就可以看作是一种更简单的进行最后一步求解的方法。
基本原理
对于任意标量函数 u ( x , y , z ) u(x,y,z) u(x,y,z)(这里以三元函数为例),其梯度定义为:
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ \operatorname{…
我们知道,梯度代表函数在给定点增加最快的方向,那么,如果我们以一个较小的步长,沿着梯度的负方向逐步前进,就可以逐渐逼近最小值点,这就是梯度下降法的基本思想。
这可以做如下类比:一个人在山坡上,想要以最快的速度下山,那么他就可以寻找山体最陡峭的方向,一小步一小步(防止摔倒)走到山谷处。
这一过程可以用数学工具描述为:
Θ i + 1 = Θ i − α ∇ J ( Θ ) (2.1.2) \Theta^{i+1} = \Theta^i - \alpha \nabla J(\Theta) \tag{2.1.2} Θi+1=Θi−α∇J(Θ)(2.1.2)
其中:
- Θ = ( θ 0 , θ 1 , ⋯ , θ n ) Θ=(θ_0,θ _1,\cdots, θ_n) Θ=(θ0,θ1,⋯,θn);
- α α α为一个较小步长或学习率(较小为了保证不错过最小值点);
- Θ i , Θ i + 1 Θ ^i, Θ ^{i+1} Θi,Θi+1分别代表当前位置和进行计算后的位置。
下面我们来以几个例子具体说明。
单变量的情形
我们先从单变量的简单情形开始讨论,并先将问题与最小二乘法的背景脱离。假设有一个单变量的函数
J ( θ ) = θ 2 + 2 (2.2.1) J(\theta) = \theta^2 + 2 \tag{2.2.1} J(θ)=θ2+2(2.2.1)
这是一个简单的抛物线,现在我们要求其最小值。
我们先求其导数(一维情形下,梯度退化为导数)
J ′ ( θ ) = 2 θ (2.2.2) J'(\theta) = 2\theta \tag{2.2.2} J′(θ)=2θ(2.2.2)
假设迭代起点为 θ 0 = 0 θ^0 = 0 θ0=0,步长设为 α = 0.4 α = 0.4 α=0.4,那么我们可以进行如下的迭代计算:
θ 0 = 1 θ 1 = θ 0 − α J ′ ( θ ) ∣ θ = θ 0 = 1 − 0.4 × 2 × 1 = 0.2 θ 2 = θ 1 − α J ′ ( θ ) ∣ θ = θ 1 = 0.2 − 0.4 × 2 × 0.2 = 0.04 θ 3 = 0.08 θ 4 = 0.0016 ⋯ (2.1.3) \begin{aligned} \theta^0 &= 1 \\ \theta^1 &= \theta^0 - \alpha J'(\theta)\Big|_{\theta = \theta^0} = 1-0.4\times 2\times 1 = 0.2 \\ \theta^2 &= \theta^1 - \alpha J'(\theta)\Big|_{\theta = \theta^1} = 0.2-0.4\times 2\times 0.2 = 0.04 \\ \theta^3 &= 0.08\\ \theta^4 &= 0.0016 \\ \cdots \end{aligned} \tag{2.1.3} θ0θ1θ2θ3θ4⋯=1=θ0−αJ′(θ)∣∣∣θ=θ0=1−0.4×2×1=0.2=θ1−αJ′(θ)∣∣∣θ=θ1=0.2−0.4×2×0.2=0.04=0.08=0.0016(2.1.3)
经过四次迭代,我们基本已经达到了最小值点。
多变量的情形
接下来我们来讨论第一节LSM问题的求解方法:
我们将线性模型的参数 a , b a,b a,b记为 θ 0 , θ 1 θ_0, θ_1 θ0,θ1。同样地,计算误差函数(这里称之为代价函数 J J J):
J ( θ 0 , θ 1 ) = 1 2 N ∑ i = 1 N ( y ^ i − y i ) 2 J(\theta_0, \theta_1) = \frac 1 {2N}\sum_{i=1}^N \left( \hat y_i-y_i \right)^2 J(θ0,θ1)=2N1i=1∑N(y^i−yi)2
其中 1 2 \dfrac 1 2 21是为了方便之后,与求导形成的“2”相抵消。
然后进行梯度下降法的求解(多变量情形与单变量完全类似,只不过需要将导数换为梯度,且标量计算变为向量计算):
任意选取一个迭代起点 Θ 0 = ( θ 0 0 , θ 1 0 ) Θ^0 = (θ^0_0, θ ^0_1) Θ0=(θ00,θ10),并选取一个合适大小的步长 α α α:
( θ 0 1 , θ 1 1 ) = ( θ 0 0 , θ 1 0 ) − α J ′ ( Θ ) ∣ Θ = ( θ 0 0 , θ 1 0 ) ( θ 0 2 , θ 1 2 ) = ( θ 0 1 , θ 1 1 ) − α J ′ ( Θ ) ∣ Θ = ( θ 0 1 , θ 1 1 ) ⋯ (2.1.4) \begin{aligned} (\theta^1_0,\theta^1_1) &= (\theta^0_0,\theta^0_1) - \alpha J'(\Theta)\Big|_{\Theta = (\theta^0_0,\theta^0_1)} \\ (\theta^2_0,\theta^2_1) &= (\theta^1_0,\theta^1_1) - \alpha J'(\Theta)\Big|_{\Theta = (\theta^1_0,\theta^1_1)} \\ \cdots \end{aligned} \tag{2.1.4} (θ01,θ11)(θ02,θ12)⋯=(θ00,θ10)−αJ′(Θ)∣∣∣Θ=(θ00,θ10)=(θ01,θ11)−αJ′(Θ)∣∣∣Θ=(θ01,θ11)(2.1.4)
即可逐步逼近最小值点,最终对应的 θ 0 , θ 1 θ_0, θ_1 θ0,θ1即为拟合参数。
牛顿法
在前面我们提到,为了令 ( 1.1 ) (1.1) (1.1)式最小,我们通过求偏导数,转化为求 ( 1.2 ) (1.2) (1.2)式的零点。我们可以将这一问题抽象:
现希望求解某一方程 f = 0 f=0 f=0的根,但并不是所有方程都有求根公式(或求根公式非常复杂),那么我们就可以使用**牛顿法(Newton’s Method)**进行迭代求解。
二维情形
若要求解方程 f ( x ) = 0 f(x)=0 f(x)=0的根,由泰勒公式
f ( x ) = f ( x 0 ) 0 ! + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + … + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n ( x ) (3.1.1) f(x)=\frac{f\left(x_{0}\right)}{0 !}+\frac{f^{\prime}\left(x_{0}\right)}{1 !}\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\ldots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_{n}(x) \tag{3.1.1} f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+…+n!f(n)(x0)(x−x0)n+Rn(x)(3.1.1)
将 f ( x ) f(x) f(x)在一个比较接近零点的 x 0 x_0 x0处进行一阶泰勒展开:
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) (3.1.2) f(x)\approx f(x_0)+f'(x_0)(x-x_0) \tag{3.1.2} f(x)≈f(x0)+f′(x0)(x−x0)(3.1.2)
并求解 f ( x ) = 0 f(x)=0 f(x)=0,得
x = x 1 = x 0 − f ( x 0 ) f ′ ( x 0 ) (3.1.3) x = x_1 = x_0 - \frac {f(x_0)}{f'(x_0)} \tag{3.1.3} x=x1=x0−f′(x0)f(x0)(3.1.3)
需要注意,这只是一个近似解,但通常可以让 x 1 x_1 x1比 x 0 x_0 x0更加接近真实的零点。继续迭代,我们便可以得出
x n + 1 = x n − f ( x n ) f ′ ( x n ) , n ≥ 0 (3.1.4) x_{n+1} = x_n - \frac {f(x_n)}{f'(x_n)} \quad,n\ge 0 \tag{3.1.4} xn+1=xn−f′(xn)f(xn),n≥0(3.1.4)
当迭代次数足够多时,就可以无限逼近真实零点。需要注意的是,使用牛顿法在求极值时,如果初始点选取不好,则可能不收敛于极小点。
而在最优化问题中,我们一般要求函数 f f f的最大、最小值,这可以转化为求解 f ’ = 0 f’ = 0 f’=0的问题,这与前面完全类似,只不过泰勒展开到二阶即可。对应的迭代公式为:
x n + 1 = x n − f ′ ( x n ) f ′ ′ ( x n ) , n ≥ 0 (3.1.5) x_{n+1} = x_n - \dfrac {f'(x_n)}{f''(x_n)} \quad,n\ge 0 \tag{3.1.5} xn+1=xn−f′′(xn)f′(xn),n≥0(3.1.5)
这恰恰与前面LSM的思想不谋而合,因而可以用于好解决尤其是非线性情况下的最小二乘问题。
高维情形
与二维情形原理类似,这里直接给出高维情形的迭代公式(梯度取代了一阶导数,而Hessian矩阵取代了二阶导数):
X n + 1 = X n − H − 1 ( f ( X n ) ) ∇ f ( X n ) , n ≥ 0 (3.2.1) X_{n+1} = X_n - \bold H^{-1} \left(f(X_n) \right)\nabla f(X_n)\quad,n\ge 0 \tag{3.2.1} Xn+1=Xn−H−1(f(Xn))∇f(Xn),n≥0(3.2.1)
其中 H \bold H H为Hessian矩阵:
H ( f ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] (3.2.2) \bold H(f)=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] \tag{3.2.2} H(f)=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎤(3.2.2)
与梯度下降法的比较
-
本质上,牛顿法是二阶收敛,梯度下降是一阶收敛,所以牛顿法收敛更快。例如,我们想找一条最短的路径走到山谷,梯度下降法每次只从当前所处位置选一个坡度最大的方向走一步,而牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部(牛顿法目光更加长远,少走弯路;相对而言,梯度下降法只考虑了局部的最优,没有全局思想);
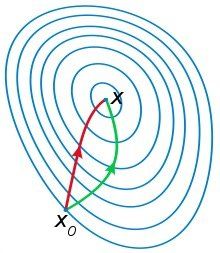
红色曲线为利用牛顿法求解,绿色曲线为利用梯度下降法求解 -
但是求解每一步都需要求解目标函数的Hessian矩阵的逆矩阵,比较复杂。
高斯-牛顿法
高斯-牛顿法(Gauss-Newton Method)实际上是牛顿法的在求解非线性最小二乘问题时的一个特例。我们的目的是,在给定 N N N组数据点 { ( x i , y j ) ∣ i = 1 , 2 , ⋯ , N } \{ (x_i,y_j)| i=1,2,\cdots, N \} {(xi,yj)∣i=1,2,⋯,N}时,拟合一条具有 M M M个参数 a = [ a 1 , ⋯ , a M ] T \bold a = [a_1,\cdots,a_M]^{\rm T} a=[a1,⋯,aM]T非线性曲线
y = f ( x , a 1 , ⋯ , a M ) ≜ f ( x , a ) (4.1) y = f(x,a_1,\cdots,a_M)\triangleq f(x,\bold a) \tag{4.1} y=f(x,a1,⋯,aM)≜f(x,a)(4.1)
我们定义 f i ( a ) = f ( x i , a ) f_i(\bold a) = f(x_i,\bold a) fi(a)=f(xi,a),残差 r i = y i − f ( x i , a ) = y i − f ( a ) ( i = 1 , ⋯ , M ) r_i = y_i - f(x_i,\bold a) = y_i - f(\bold a)\quad(i=1,\cdots,M) ri=yi−f(xi,a)=yi−f(a)(i=1,⋯,M),并可以将之写为矩阵形式:
r = [ r 1 ⋮ r N ] = [ y 1 − f 1 ( a ) ⋮ y N − f N ( a ) ] = [ y 1 ⋮ y N ] − [ f 1 ( a ) ⋮ f N ( a ) ] = y − f ( a ) (4.2) \mathbf{r}=\left[\begin{array}{c} r_{1} \\ \vdots \\ r_{N} \end{array}\right]=\left[\begin{array}{c} y_{1}-f_{1}(\mathbf{a}) \\ \vdots \\ y_{N}-f_{N}(\mathbf{a}) \end{array}\right]=\left[\begin{array}{c} y_{1} \\ \vdots \\ y_{N} \end{array}\right]-\left[\begin{array}{c} f_{1}(\mathbf{a}) \\ \vdots \\ f_{N}(\mathbf{a}) \end{array}\right]=\mathbf{y}-\mathbf{f}(\mathbf{a}) \tag{4.2} r=⎣⎢⎡r1⋮rN⎦⎥⎤=⎣⎢⎡y1−f1(a)⋮yN−fN(a)⎦⎥⎤=⎣⎢⎡y1⋮yN⎦⎥⎤−⎣⎢⎡f1(a)⋮fN(a)⎦⎥⎤=y−f(a)(4.2)
那么,误差函数就可以写为
ε ( a ) = ∑ i = 1 N r i 2 = r T r = ∥ r ∥ 2 = ∥ y − f ( a ) ∥ 2 (4.3) \begin{aligned} \varepsilon(\mathbf{a})=\sum_{i=1}^{N} r_{i}^{2}=\mathbf{r}^{{\rm T}} \mathbf{r}=\|\mathbf{r}\|^{2}=\|\mathbf{y}-\mathbf{f}(\mathbf{a})\|^{2} \end{aligned} \tag{4.3} ε(a)=i=1∑Nri2=rTr=∥r∥2=∥y−f(a)∥2(4.3)
使得 ε ( a ) \varepsilon(\bold a) ε(a)最小的最佳参数 a \bold a a应满足梯度向量为0:
∂ ∂ a j ε ( a ) = ∂ ∂ a j ∑ i = 1 N [ y i − f i ( a ) ] 2 = − 2 ∑ i = 1 N [ y i − f i ( a ) ] ∂ f i ( a ) ∂ a j = − 2 ∑ i = 1 [ y i − f i ( a ) ] J i j = 0 ( j = 1 , ⋯ , M ) (4.4-1) \begin{aligned} \frac{\partial}{\partial a_{j}} \varepsilon(\mathbf{a})&=\frac{\partial}{\partial a_{j}} \sum_{i=1}^{N}\left[y_{i}-f_{i}(\mathbf{a})\right]^{2}=-2 \sum_{i=1}^{N}\left[y_{i}-f_{i}(\mathbf{a})\right] \frac{\partial f_{i}(\mathbf{a})}{\partial a_{j}}\\ &=-2 \sum_{i=1}\left[y_{i}-f_{i}(\mathbf{a})\right] J_{i j}=0 \end{aligned}(j=1, \cdots, M) \tag{4.4-1} ∂aj∂ε(a)=∂aj∂i=1∑N[yi−fi(a)]2=−2i=1∑N[yi−fi(a)]∂aj∂fi(a)=−2i=1∑[yi−fi(a)]Jij=0(j=1,⋯,M)(4.4-1)
对应的向量形式:
g ( ε ( a ) ) = d d a ε ( a ) = d d a ∥ y − f ( a ) ∥ 2 = − 2 J T ( y − f ( a ) ) = 0 (4.4-2) \mathbf{g}(\varepsilon(\mathbf{a}))=\frac{d}{d \mathbf{a}} \varepsilon(\mathbf{a})=\frac{d}{d \mathbf{a}}\|\mathbf{y}-\mathbf{f}(\mathbf{a})\|^{2}=-2 \mathbf{J}^{T}(\mathbf{y}-\mathbf{f}(\mathbf{a}))=\mathbf{0} \tag{4.4-2} g(ε(a))=dadε(a)=dad∥y−f(a)∥2=−2JT(y−f(a))=0(4.4-2)
其中 J \bold J J是Jacobian矩阵
J = [ ∂ f 1 ( a ) ∂ a 1 ∂ f 1 ( a ) ∂ a 2 ⋯ ∂ f 1 ( a ) ∂ a M ∂ f 2 ( a ) ∂ a 1 ∂ f 2 ( a ) ∂ a 2 ⋯ ∂ f 2 ( a ) ∂ a M ⋮ ⋮ ⋱ ⋮ ∂ f N ( a ) ∂ a 1 ∂ f N ( a ) ∂ a 2 ⋯ ∂ f N ( a ) ∂ a M ] (4.5) \bold J = \begin{bmatrix} \frac{\partial f_{1}(\mathbf{a})}{\partial a_{1}} & \frac{\partial f_{1}(\mathbf{a})}{\partial a_{2}} & \cdots & \frac{\partial f_{1}(\mathbf{a})}{\partial a_{M}} \\ \frac{\partial f_{2}(\mathbf{a})}{\partial a_{1}} & \frac{\partial f_{2}(\mathbf{a})}{\partial a_{2}} & \cdots & \frac{\partial f_{2}(\mathbf{a})}{\partial a_{M}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_{N}(\mathbf{a})}{\partial a_{1}} & \frac{\partial f_{N}(\mathbf{a})}{\partial a_{2}} & \cdots & \frac{\partial f_{N}(\mathbf{a})}{\partial a_{M}} \end{bmatrix} \tag{4.5} J=⎣⎢⎢⎢⎢⎡∂a1∂f1(a)∂a1∂f2(a)⋮∂a1∂fN(a)∂a2∂f1(a)∂a2∂f2(a)⋮∂a2∂fN(a)⋯⋯⋱⋯∂aM∂f1(a)∂aM∂f2(a)⋮∂aM∂fN(a)⎦⎥⎥⎥⎥⎤(4.5)
但求导置零的方法不一定能得到闭合形式的解,因而我们采用迭代的方法:
a n + 1 = a n + Δ a (4.6) \mathbf{a}_{n+1}=\mathbf{a}_{n}+\Delta \mathbf{a} \tag{4.6} an+1=an+Δa(4.6)
为了找到 Δ a = a n + 1 − a n = [ Δ a 1 , ⋯ , Δ a M ] T \Delta \mathbf{a}=\mathbf{a}_{n+1}-\mathbf{a}_{n}=\left[\Delta a_{1}, \cdots, \Delta a_{M}\right]^{{\rm T}} Δa=an+1−an=[Δa1,⋯,ΔaM]T,我们考虑 f i ( a n + 1 ) f_i(\bold a_{n+1}) fi(an+1)在 a n \bold a_n an处的一阶泰勒展开式:
f i ( a n + 1 ) ≈ f i ( a n ) + ∑ k = 1 M ∂ f i ( a n ) ∂ a k Δ a k = f i ( a n ) + ∑ k = 1 M J i k Δ a k , ( i = 1 , ⋯ , N ) (4.7-1) f_{i}\left(\mathbf{a}_{n+1}\right) \approx f_{i}\left(\mathbf{a}_{n}\right)+\sum_{k=1}^{M} \frac{\partial f_{i}\left(\mathbf{a}_{n}\right)}{\partial a_{k}} \Delta a_{k}=f_{i}\left(\mathbf{a}_{n}\right)+\sum_{k=1}^{M} J_{i k} \Delta a_{k}, \quad(i=1, \cdots, N) \tag{4.7-1} fi(an+1)≈fi(an)+k=1∑M∂ak∂fi(an)Δak=fi(an)+k=1∑MJikΔak,(i=1,⋯,N)(4.7-1)
也就是:
f ( a n + 1 ) ≈ f ( a n ) + J Δ a (4.7-2) \mathbf{f}\left(\mathbf{a}_{n+1}\right) \approx \mathbf{f}\left(\mathbf{a}_{n}\right)+\mathbf{J} \Delta \mathbf{a} \tag{4.7-2} f(an+1)≈f(an)+JΔa(4.7-2)
将这一关系代入 ( 4.4 − 1 ) (4.4-1) (4.4−1)中:
∑ i = 1 N [ y i − f i ( a n + 1 ) ] J i j ≈ ∑ i = 1 N [ y i − f i ( a n ) − ∑ k = 1 M J i k Δ a k ] J i j = 0 ∑ i = 1 N J i j ∑ k = 1 M J i k Δ a k = ∑ i = 1 N J i j [ y i − f i ( a n ) ] ( j = 1 , ⋯ , M ) (4.8-1) \begin{aligned} \sum_{i=1}^{N}\left[y_{i}-f_{i}\left(\mathbf{a}_{n+1}\right)\right] J_{i j} &\approx \sum_{i=1}^{N}\left[y_{i}-f_{i}\left(\mathbf{a}_{n}\right)-\sum_{k=1}^{M} J_{i k} \Delta a_{k}\right] J_{i j}=0 \\ \sum_{i=1}^{N} J_{i j} \sum_{k=1}^{M} J_{i k} \Delta a_{k} &= \sum_{i=1}^{N} J_{i j}\left[y_{i}-f_{i}\left(\mathbf{a}_{n}\right)\right] \end{aligned} \quad(j=1, \cdots, M) \tag{4.8-1} i=1∑N[yi−fi(an+1)]Jiji=1∑NJijk=1∑MJikΔak≈i=1∑N[yi−fi(an)−k=1∑MJikΔak]Jij=0=i=1∑NJij[yi−fi(an)](j=1,⋯,M)(4.8-1)
写为矩阵形式:
( J T J ) △ a = J T ( y − f ( a n ) ) (4.8-2) \left(\mathbf{J}^{{\rm T}} \mathbf{J}\right) \triangle \mathbf{a}=\mathbf{J}^{{\rm T}}\left(\mathbf{y}-\mathbf{f}\left(\mathbf{a}_{n}\right)\right) \tag{4.8-2} (JTJ)△a=JT(y−f(an))(4.8-2)
这样的好处是可以方便地对 a \bold a a进行求解:
Δ a = a n + 1 − a n = ( J T J ) − 1 J T ( y − f ( a n ) ) = J − ( y − f ( a n ) ) (4.9) \Delta \mathbf{a}=\mathbf{a}_{n+1}-\mathbf{a}_{n}=\left(\mathbf{J}^{T} \mathbf{J}\right)^{-1} \mathbf{J}^{T}\left(\mathbf{y}-\mathbf{f}\left(\mathbf{a}_{n}\right)\right)=\mathbf{J}^{-}\left(\mathbf{y}-\mathbf{f}\left(\mathbf{a}_{n}\right)\right) \tag{4.9} Δa=an+1−an=(JTJ)−1JT(y−f(an))=J−(y−f(an))(4.9)
其中 J − = ( J T J ) − 1 J T \bold J ^{-} = \left(\bold J^{\rm T}\bold J\right)^{-1}\bold J ^ {{\rm T}} J−=(JTJ)−1JT为 J \bold J J的伪逆矩阵。这样我们就得到了迭代表达式:
a n + 1 = a n + Δ a = a n + J − ( y − f ( a n ) ) = a n − J − ( f ( a n ) − y ) (4.10) \mathbf{a}_{n+1}=\mathbf{a}_{n}+\Delta \mathbf{a}=\mathbf{a}_{n}+\mathbf{J}^{-}\left(\mathbf{y}-\mathbf{f}\left(\mathbf{a}_{n}\right)\right)=\mathbf{a}_{n}-\mathbf{J}^{-}\left(\mathbf{f}\left(\mathbf{a}_{n}\right)-\mathbf{y}\right) \tag{4.10} an+1=an+Δa=an+J−(y−f(an))=an−J−(f(an)−y)(4.10)
有了迭代公式,我们自然就可以更简便地求解导数置零的问题,应用于最小二乘问题中也就可以大大简化计算并解决LSM无法解决的非线性问题。
参考文献
-
最小二乘法和梯度下降法有哪些区别? - 任妍Carol的回答 - 知乎
-
梯度下降算法原理讲解——机器学习
-
Newton法(牛顿法 Newton Method)
-
【math】梯度下降法(梯度下降法,牛顿法,高斯牛顿法,Levenberg-Marquardt算法)
-
Gauss-Newton algorithm for nonlinear models