独家连载 | 梯度消失和梯度爆炸
4.6 梯度消失与梯度爆炸
4.6.1 梯度消失
根据上文BP算法中的推导,我们从公式4.44,4.45,4.46中可以知道,权值的调整ΔW是跟学习信号δ相关的。同时我们从4.41,4.42,4.43中可以知道在学习信号δ表达式中存在f ’ (x)。也就是说激活函数的导数会影响学习信号δ的值,而学习信号δ的值会影响权值调整ΔW的值。那么激活函数的值越大,ΔW的值就越大;激活函数的值越小,ΔW的值也就越小。
假设激活函数为sigmoid函数,前文中我们已经知道了sigmoid函数的表达式为: f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1,sigmoid函数的导数为: f ′ ( x ) = f ( x ) [ 1 − f ( x ) ] f ' (x) = f(x)[1-f(x)] f′(x)=f(x)[1−f(x)],我们可以画出sigmoid函数的导数图像为图4.18:
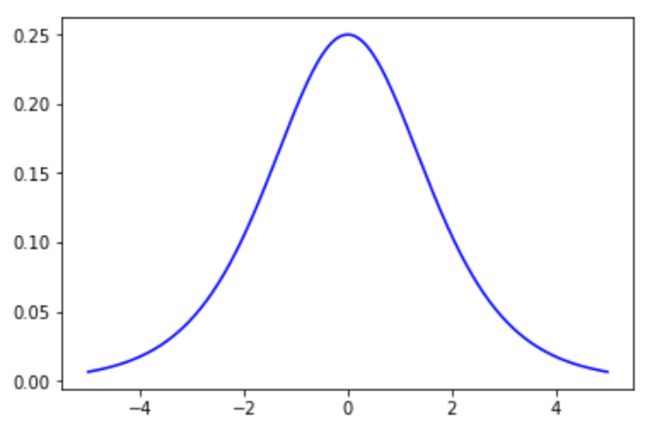
这里我们发现当x=0时,sigmoid函数导数可以取得最大值0.25。x取值较大或较小时,sigmoid函数的导数很快就趋向于0。不管怎么样,sigmoid函数的导数都是一个小于1的数,学习信号δ乘以一个小于1的数,那么δ就会减小。学习信号从输出层一层一层向前反向传播的时候,每传播一层学习信号就会变小一点,经过多层传播后,学习信号就会接近于0,从而使得权值ΔW调整接近于0。ΔW接近于0那就意味着该层的参数不会发生改变,不能进行优化。参数不能优化,那整个网络就不能再进行学习了。学习信号随着网络传播逐渐减小的问题也被称为**梯度消失(vanishing gradient)**的问题。
我们再考虑一下tanh函数的导数,tanh函数的表达式为: f ( x ) = e x − e − x e x + e − x f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=ex+e−xex−e−x,tanh函数的导数为: f ′ ( x ) = 1 − ( f ( x ) ) 2 f ' (x) = 1- (f(x))^2 f′(x)=1−(f(x))2 ,tanh函数的导数如图4.19:
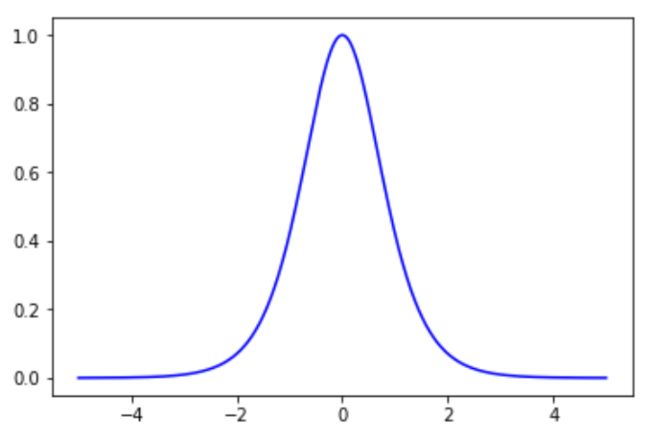
t a n h tanh tanh函数导数图像看起来比sigmoid函数要好一些,x=0时, t a n h tanh tanh函数导数可以取得最大值1。x取值较大或较小时, t a n h tanh tanh函数的导数很快就趋向于0。不管怎么样, t a n h tanh tanh函数导数的取值总是小于1的,所以tanh作为激活函数也会存在梯度消失的问题。
对于softsign函数,softsign函数的表达式为: f ( x ) = x 1 + ∣ x ∣ f(x)=\frac{x}{1+|x|} f(x)=1+∣x∣x,softsign函数的导数为: f ′ ( x ) = 1 ( 1 + ∣ x ∣ ) 2 f '(x)=\frac{1}{(1+|x|)^2} f′(x)=(1+∣x∣)21,softsign函数的导数如图4.20:
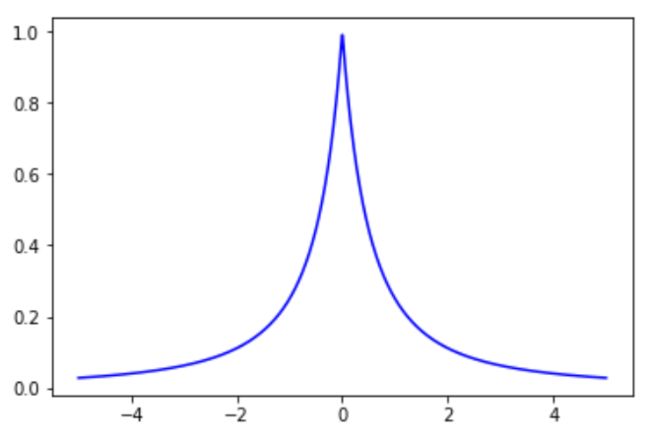
softsign函数x=0时,softsign函数导数可以取得最大值1。x取值较大或较小时,softsign函数的导数很快就趋向于0。不管怎么样,softsign函数导数的取值总是小于1的,所以softsign作为激活函数也会存在梯度消失的问题。
4.6.2 梯度爆炸
当我们使用sigmoid,tanh和softsign作为激活函数时,它们的导数取值范围都是小于等于1的,所以会产生梯度消失的问题。那么我们可能会想到,如果使用导数大于1的函数作为激活函数,情况会如何?
如果学习信号δ乘以一个大于1的数,那么δ就会变大。学习信号从输出层一层一层向前反向传播的时候,每传播一层学习信号就会变大一点,经过多层传播后,学习信号就会接近于无穷大,从而使得权值ΔW调整接近于无穷大。ΔW接近于无穷大那就意味着该层的参数,处于一种极不稳定的状态,那么网络就不能正常工作了。学习信号随着网络传播逐渐增大的问题也被称为**梯度爆炸(exploding gradient)**的问题。
4.6.3 使用ReLU函数解决梯度消失和梯度爆炸的问题
我们知道ReLU的表达式为:f(x) = max(0,x)。当x小于0时,f(x)的取值为0;当x大于0时,f(x)的取值等于x。ReLU函数的导数如图4.21:
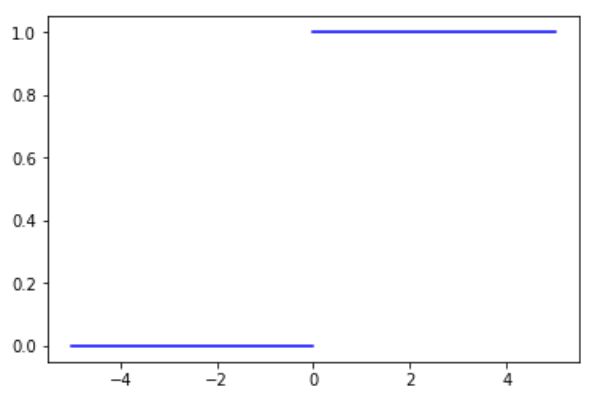
前面我们讨论了当激活函数的导数小于1时,网络会产生梯度消失,激活函数的导数大于1时,网络会产生梯度爆炸。那么当我们使用ReLU作为激活函数的时候,x小于0时,ReLU的导数为0;x大于0时,ReLU的导数为1。导数为1是一个很好的特性,不会使得学习信号越来越小,也不会让学习信号越来越大,可以让学习信号比较稳定地从后向前传播。解决了梯度消失和梯度爆炸的问题,同时计算方便,可以加速网络的训练。
ReLU也存在缺点,由于x小于0的部分f(x)的取值恒定为0,会导致一些神经元无法激活。
不过总的来说,ReLU还是优点大于缺点的,所以在一些比较深层的神经网络中,通常都会使用ReLU作为神经网络的激活函数。
除此之外可能我们还会想到线性激活函数y = x 的导数也是等于1,也可以克服梯度消失和梯度爆炸的问题。不过之前我们也多次提到线性激活函数不会能描绘非线性的分类边界,所以无法处理非线性问题。因此线性函数依旧不算是一个好的激活函数。
