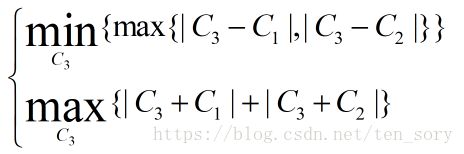数据挖掘十大算法（二）：K-means聚类算法原理与实现

参考：

1.机器学习-KMeans聚类 K值以及初始类簇中心点的选取

2.K-Means算法的研究分析及改进

一、K-means算法原理

K-means算法是最常用的一种聚类算法。算法的输入为一个样本集（或者称为点集），通过该算法可以将样本进行聚类，具有相似特征的样本聚为一类。

针对每个点，计算这个点距离所有中心点最近的那个中心点，然后将这个点归为这个中心点代表的簇。一次迭代结束之后，针对每个簇类，重新计算中心点，然后针对每个点，重新寻找距离自己最近的中心点。如此循环，直到前后两次迭代的簇类没有变化。

下面通过一个简单的例子，说明K-means算法的过程。如下图所示，目标是将样本点聚类成3个类别。

基本的步骤为：

step1：选定要聚类的类别数目k（如上例的k=3类），选择k个中心点。

step2：针对每个样本点，找到距离其最近的中心点（寻找组织），距离同一中心点最近的点为一个类，这样完成了一次聚类。

step3：判断聚类前后的样本点的类别情况是否相同，如果相同，则算法终止，否则进入step4。

step4：针对每个类别中的样本点，计算这些样本点的中心点，当做该类的新的中心点，继续step2。

上述步骤的关键两点是：

1. 找到距离自己最近的中心点。

2. 更新中心点。

二、Python实现

下面给出它的Python实现，其中中心点的选取是手动选择的。在代码中随机产生了一个样本，用于测试K-means算法：

# K-means Algorithm is a clustering algorithm
import numpy as np
import matplotlib.pyplot as plt
import random


def get_distance(p1, p2):
    diff = [x-y for x, y in zip(p1, p2)]
    distance = np.sqrt(sum(map(lambda x: x**2, diff)))
    return distance


# 计算多个点的中心
# cluster = [[1,2,3], [-2,1,2], [9, 0 ,4], [2,10,4]]
def calc_center_point(cluster):
    N = len(cluster)
    m = np.matrix(cluster).transpose().tolist()
    center_point = [sum(x)/N for x in m]
    return center_point


# 检查两个点是否有差别
def check_center_diff(center, new_center):
    n = len(center)
    for c, nc in zip(center, new_center):
        if c != nc:
            return False
    return True


# K-means算法的实现
def K_means(points, center_points):

    N = len(points)         # 样本个数
    n = len(points[0])      # 单个样本的维度
    k = len(center_points)  # k值大小

    tot = 0
    while True:             # 迭代
        temp_center_points = [] # 记录中心点

        clusters = []       # 记录聚类的结果
        for c in range(0, k):
            clusters.append([]) # 初始化

        # 针对每个点，寻找距离其最近的中心点（寻找组织）
        for i, data in enumerate(points):
            distances = []
            for center_point in center_points:
                distances.append(get_distance(data, center_point))
            index = distances.index(min(distances)) # 找到最小的距离的那个中心点的索引，

            clusters[index].append(data)    # 那么这个中心点代表的簇，里面增加一个样本

        tot += 1
        print(tot, '次迭代   ', clusters)
        k = len(clusters)
        colors = ['r.', 'g.', 'b.', 'k.', 'y.']  # 颜色和点的样式
        for i, cluster in enumerate(clusters):
            data = np.array(cluster)
            data_x = [x[0] for x in data]
            data_y = [x[1] for x in data]
            plt.subplot(2, 3, tot)
            plt.plot(data_x, data_y, colors[i])
            plt.axis([0, 1000, 0, 1000])

        # 重新计算中心点（该步骤可以与下面判断中心点是否发生变化这个步骤，调换顺序）
        for cluster in clusters:
            temp_center_points.append(calc_center_point(cluster))

        # 在计算中心点的时候，需要将原来的中心点算进去
        for j in range(0, k):
            if len(clusters[j]) == 0:
                temp_center_points[j] = center_points[j]

        # 判断中心点是否发生变化：即，判断聚类前后样本的类别是否发生变化
        for c, nc in zip(center_points, temp_center_points):
            if not check_center_diff(c, nc):
                center_points = temp_center_points[:]   # 复制一份
                break
        else:   # 如果没有变化，那么退出迭代，聚类结束
            break

    plt.show()
    return clusters # 返回聚类的结果




# 随机获取一个样本集，用于测试K-means算法
def get_test_data():

    N = 1000

    # 产生点的区域
    area_1 = [0, N / 4, N / 4, N / 2]
    area_2 = [N / 2, 3 * N / 4, 0, N / 4]
    area_3 = [N / 4, N / 2, N / 2, 3 * N / 4]
    area_4 = [3 * N / 4, N, 3 * N / 4, N]
    area_5 = [3 * N / 4, N, N / 4, N / 2]

    areas = [area_1, area_2, area_3, area_4, area_5]
    k = len(areas)

    # 在各个区域内，随机产生一些点
    points = []
    for area in areas:
        rnd_num_of_points = random.randint(50, 200)
        for r in range(0, rnd_num_of_points):
            rnd_add = random.randint(0, 100)
            rnd_x = random.randint(area[0] + rnd_add, area[1] - rnd_add)
            rnd_y = random.randint(area[2], area[3] - rnd_add)
            points.append([rnd_x, rnd_y])

    # 自定义中心点，目标聚类个数为5，因此选定5个中心点
    center_points = [[0, 250], [500, 500], [500, 250], [500, 250], [500, 750]]

    return points, center_points


if __name__ == '__main__':

    points, center_points = get_test_data()
    clusters = K_means(points, center_points)
    print('#######最终结果##########')
    for i, cluster in enumerate(clusters):
        print('cluster ', i, ' ', cluster)

由于样本点是随机产生的，所以每次运行的结果不相同。6次迭代得到的聚类结果分别如下图。

控制台输出结果为：

三、初始中心点的选取

初始中心点的选取，对聚类的结果影响较大。可以验证，不同初始中心点，会导致聚类的效果不同。如何选择初始中心点呢？一个原则是：

初始中心点之间的间距应该较大。因此，可以采取的策略是：

step1：计算所有样本点之间的距离，选择距离最大的一个点对（两个样本C1, C2）作为2个初始中心点，从样本点集中去掉这两个点。

step2：如果初始中心点个数达到k个，则终止。如果没有，在剩余的样本点中，选一个点C3，这个点优化的目标是：

这是一个双目标优化问题，可以约束其中一个，极值化另外一个，这样可以选择一个合适的C3点，作为第3个初始中心点。

如果要寻找第4个初始中心点，思路和寻找第3个初始中心点是相同的。

四、误差平方和（Sum of Squared Error）

误差平法和，SSE，用于评价聚类的结果的好坏，SSE的定义如下。

一般情况下，k越大，SSE越小。假设k=N=样本个数，那么每个点自成一类，那么每个类的中心点为这个类中的唯一一个点本身，那么SSE=0。

五、k值得确定

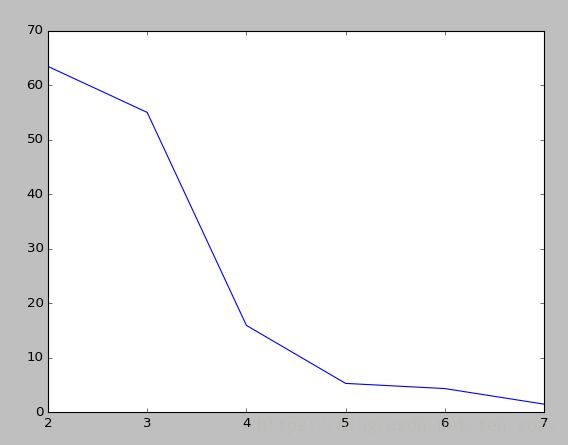
一般k不会很大，大概在2~10之间，因此可以作出这个范围内的SSE-k的曲线，再选择一个拐点，作为合适的k值。

可以看到，k=5之后，SSE下降的变得很缓慢了，因此最佳的k值为5。