NOIP2017 国庆郑州集训知识梳理汇总

第一天  基础算法及数学

基本算法

递推、递归、分治 
二分、倍增 
贪心

递推

指通过观察、归纳，发现较大规模问题和较小规模问题之间的关系，用一些数学公式表达出来

在一些题解中，和“计数DP”是指同一个概念

看例题

例 1

用 1 * 2 的骨牌，覆盖 2 * n 的棋盘的方案数？

解：很经典的Fibonacci 数 
O(n) 求解

例 2

长度为 2n 的合法括号序列个数 
合法括号序的定义： 
空串合法 
若 A 合法，则 ( A ) 合法； 
若 A 和 B 合法，则 AB 也合法。

解：比较经典的Catalan 数 
O(n ^ 2) 求解 
可以优化到 O(n) - O(1)

对于一个左括号 一定有唯一右括号与其匹配

例 3

有 n 个人 
你想把他们划分为若干个小组，每个小组至少有一个人，每个人恰好属于一个组 
问方案数 
定义两种方案是不同的，当且仅当存在一个小组，只在其中一个方案出现

解：Bell 数 
B[n+1] = sum { 0<=k<=n } C(n, k) * B[k]

例 4

求排列 P 的数量，满足 P[i] != i

解：错位排列数 
容斥或者递推求

递归

所谓递归，是指函数“自己调用自己”的一种编程方法 
在解决一个问题时，如果发现问题能拆解为一个或多个相同规模的子问题时，就可以考虑使用这种方法求解

例 - 汉诺塔

有三个柱子 
有 n 个圆盘从小到大依次叠在一个柱子上 
你希望通过若干步，把它们移动到另一个柱子上 
移动规则： 
每次可以移动一个圆盘 
任意时候，大圆盘不能在小圆盘上方

解： 
解决规模为 n 的问题可以分三步： 
把 n-1 个圆盘移动到另一个柱子上 
把大圆盘移动到第三个柱子上 
把 n-1 个圆盘移动到大圆盘上 
注意到第 1 和第 3 步是相同形式、规模更小的子问题 
于是可以设计递归算法

二分 
倍增 
贪心 
详见专题博客…..

OI中的数学

即数论啊什么的 还有各种定理 反正我是听的糊里糊涂的的的

吕欣大佬给我们讲了： 
模算术、Bezout 定理、欧几里德算法 
素数和筛法、常见数论定理 
积性函数和Dirichlet卷积

模算术

模意义下的加减乘除 
逆元的若干种求法 
同余关系、剩余类

bezout 定理

我们阐述 Bezout 定理： 
方程 ax + by = c 有解，当且仅当 gcd(a, b) | c 
定理的证明：必要性显然，充分性见下一页

ps：gcd为求最小公约数

欧几里得算法

gcd(a, b) = gcd(a - b, b) 
证明比较简单 
事实上，定理直接给出了一种计算 gcd 的方式，直接根据上述公式计算，复杂度 O(\log min(a, b))

扩展欧几里得算法

事实上，我们可以直接在欧几里德算法求解 gcd(a, b) 的过程中，构造一组 ax + by = gcd(a, b) 的解 
这个方法依赖于递归的思想 
边界：b = 0 时, a * 1 + b * 0 = gcd(a, b) 
设我们找到了一组 bx + (a % b)y = gcd(a, b) 的解，那么： 
bx + (a - [a / b] * b]) y = gcd(a, b) ==> 
ay + b * (x - [a / b] * y) = gcd(a, b) 
令 x’ = y, y’ = (x - [a / b] * y)，可以得到： 
ax’ + by’ = gcd(a, b)

二元一次不定方程的通解

令 d = gcd(a, b) 
当我们求出 ax + by = c 的一组解 x0、y0 之后 
方程的通解具有以下形式： 
x = x0 + k * (b / d) 
y = y0 - k * (a / d) 
直观理解一下，这是一个设法让正负互相抵消的过程

素数

定义：大于 1 的、只被 1 和它本身整除的正整数称为素数 
唯一分解定理，又称算术基本定理： 
对于正整数 n，我们一定可以将其写为若干个质数的幂的乘积形式，即 
n = ∏ (pi ^ ai)，其中 pi 为质数 
并且，这种分解是唯一的

素数筛法

在解数论题的过程中，我们常常需要知道小范围内的素数的分布情况（区间内的素数个数、判断某个数是不是素数…） 
埃拉托斯特尼筛 
欧拉筛 
* 杜老师筛（什么破名字QWQ），洲阁筛

埃氏筛

（很有用） 
如果我们要筛出 [1, n] 内的所有素数，使用 [1, √n] 内的素数去筛就可以了 
设数组 mark[]，mark[i] 表示 i 是否被某个素数筛过 
从 2 开始枚举每个数 i： 
若 mark[i] = 0，表示 i 没有更小的素因子，从而知道 i 是素数。枚举 i 的所有倍数 j，令 mark[j] = 1 
若 mark[i] = 1，知道 i 是一个合数 
复杂度 O(n\lg\lg n)

埃氏筛的复杂度上界为 O(n lglg n) 
这个证明比较复杂，我们这里只证明其复杂度不超过 O(n\log n)： 
定义调和数 Hn = (1 / 1 + 1 / 2 + … + 1 / n) 
我们有 Hn ~ ln n （不严谨地，可以考虑导数帮助理解） 
对于 <= √n 的一个素数 p，我们用它去筛合数的计算量为 n / p 
于是总计算量为 n * (∑ { 1 / p | p < √n } ) <= n * H_n <= O(n\log n) 
PS：Hn ~ ln n 是一个很重要的结论，以后我们还会多次见到它

埃氏筛的应用

在进行筛法的同时，我们可以对 [1, n] 内的合数进行素数分解，从而完成一些其他工作 
例如，对于一个素数 i，枚举它的倍数 j 时，把 j 中的所有因子 i 除干净，就知道 j 的质因子分解中 i 的幂了 
有一类问题，需要你预处理区间 [L, R] 内的素数分布 
其中 R - L <= 10^6, R <= 10^10 
此时，区间 [L, R] 的长度比较小；另一方面，√R <= 10^5。我们就可以考虑使用埃氏筛的思想来求解问题 
用一个数组 mark2[] 维护区间 [L, R] 被筛的结果，用素数 p 去筛 [L, R] 的计算量为 (R - L) / p，总计算复杂度大概为 H_{R-L}，即 O((R - L) \log R)

威尔逊定理

p 是质数的充要条件为 
(p - 1)! ≡ -1 (mod p) 
充分性： 
若 p 不是质数，则 gcd( (p-1)!, p ) > 1，与 Bezout 定理相悖 
必要性： 
考虑 [1, p) 中的某个数 x 和它的乘法逆元 y 
如果 x != y, 那么 xy ≡ 1，可以令它们互相抵消 
于是只需要考虑 x 是自己的逆元的情况 
解 x^2 ≡ 1 ==> p | (x - 1) * (x + 1) 
因为 p 是质数，只有可能是 x ≡ ±1，得证

欧拉函数

欧拉函数 ��(n)，表示不大于 n 的、与 n 互质的正整数个数 
令 n = ∏ (pi^ai)，则 ��(n) = n * ∏ (1 - 1/pi) 
计算方法： 
对 n 进行质因子分解的过程中维护，O(√n) 
埃氏筛的时候顺便维护，复杂度同埃氏筛

关于欧拉函数的两个公式

∑ { ��(d) | d | n } = n 
证明：在 [1, n] 中，恰好有 ��(d) 个数和 n 的 gcd 为 n / d 
n > 1 时, ∑ { d | gcd(d, n) = 1 } = n * ��(n) / 2 
证明：当 gcd(x, n) = 1 时，可得 gcd(n - x, n) = 1，可以将与 n 互质的数两两配对 
对于 n <= 2 的情况，特殊讨论

HAOI 2012 外星人

给定 N 的质因数分解，问 N 取过多少次 �� 之后变成 1 
N 有至多 50 个质因数，每个质因数 <= 10^5，每个质因数的幂 <= 10^9

解： 
所有质因数最后都要变成若干个 2，然后消失 
每次只能消去一个 2 
除了 N 为奇数的第一次运算，每次运算一定能消去一个 2 
只有某一轮里有奇质数，一定能贡献一个 2 
于是问题转化为，每个质因子最后会贡献多少个 2 
递推即可

剩余系

剩余类： 
给定 n，整数按照模 n 取值的不同，可以分为 n 个子集，称为剩余类 
剩余系： 
给定 n，从模 n 的 n 个剩余类中各取一个数构成的集合，称为模 n 的一个剩余系，剩余系一般指完全剩余系 
简化剩余系： 
也称既约剩余系，是模 n 的完全剩余系的一个子集，其中每个元素与n 互素 
容易验证，简化剩余系中恰好有 ��(n) 个元素

欧拉定理

考虑模 n 的一个简化剩余系 S 
因为 S 中的每个元素和 n 互质，它们在模 n 意义下存在乘法逆元 
任取一个 a，使得 (a, n) = 1 
考虑集合 T = { ax | x ∈ S } 
容易验证： 
|T| = |S|，且 |T| 中的数模 n 互不同余 
|T| 中的数均和 n 互质 
由此，可得 T 也是模 n 的一个简化剩余系

因为 S 和 T 均为模 n 的简系，可得： 
∏ {x | x ∈ S} ≡ ∏ {y | y ∈ T} ==> 
∏ {x | x ∈ S} ≡ ∏ {ax | x ∈ S} ==> 
∏ {x | x ∈ S} ≡ a ^ {|S|} * ∏ {x | x ∈ S} ==> 
a^{|S|} ≡ 1 
这就是欧拉定理： 
若 (a, n) = 1，则 a ^ ��(n) ≡ 1

欧拉定理EXT

由欧拉定理可以推导出一些很有用的结论 
费马小定理： 
若 p 是质数且 (a, p) = 1，则 a ^ (p-1) ≡ 1 (mod p) 
一个应用：a ^ (p - 2) ≡ 1 / a (mod p)，可以通过快速幂求逆元 
欧拉定理 EXT： 
若 (a, p) = 1，则 a ^ x ≡ a ^ (x % ��(p)) (mod p) 
任何情况下，若 x > ��(p)，则 a ^ x ≡ a ^ (x % ��(p) + ��

eg：

BZOJ 3884 上帝与集合的正确用法

T 组询问 
每组询问给出 P，求： 
2 ^ (2 ^ (2 ^ (…) ) ) (mod P) 
T <= 1000 
P <= 10^7

解： 
由欧拉定理EXT，问题可以转化为求指数部分 mod ��(p) 
这实际上是一个相同形式的子问题，递归求解即可 
一个有趣的推论： 
对于一个数 x，不断执行 x = c^x 
在模 P 意义下，O(\log P) 次操作之后，x 变成一个常数 
SH/JL/LN/HE/SX/HL OI 2017 相逢是问候

中国剩余定理

可以用来求解这样的同余方程组： 
给定长度为 k 的数组 a[] 和数组 m[]，求解 
x ≡ a[i] (mod m[i]) 
保证 m[i] 两两互质 
解的存在性？唯一性？求法？

推导

定理：令 M = ∏ (m[i])，方程在 [0, M) 中有唯一解 x0，并且通解具有 kM + x0 的形式 
这里证明唯一性： 
设 x1 != x2 是方程的两个解，我们有 
x1 - x2 ≡ 0 (mod m[i]) 
x1 - x2 是每个 m[i] 的倍数，它们必然也是 M 的倍数，即 M | x1 - x2 
于是，x1 和 x2 最多只有一个落在区间 [0, M) 中 
解的存在性，我们通过一种构造算法来证明

构造解

令 Mi = M / m[i]，因为 (M[i], m[i]) = 1，我们可以找到 Mi 模 m[i] 的乘法逆元 t[i] 
考察 Mi * t[i]： 
j = i 时，M[i] * t[i] ≡ 1 (mod m[j]) 
j != i 时，M[i] * t[i] ≡ 0 (mod m[j]) 
令 x = ∑ (a[i] * M[i] * t[i]) 
不难验证，x 是满足要求的

模数不互质

模数不互质的时候，怎么办？ 
将方程两两合并，考虑方程组： 
x ≡ a1 (mod m1) 
x ≡ a2 (mod m2) 
令 x = k1 * m1 + a1 = k2 * m2 + a2 
则有 k1 * m1 - k2 * m2 = a2 - a1 
由 Bezout 定理判断解的存在性，用 extend_gcd 解方程即可 
事实上，可以得到一个推论： 
如果存在解，则 x 在 [0, lcm(m1, m2) ) 中有唯一解

应用

可以直接解决一类问题 
有些数学计算题，给出的模数 m 并不是一个素数 
而很多计算在模素数（或素数的幂）下会方便很多 
于是可以将 m 分解质因数，求答案模每个素数（的幂）的值，最后使用中国剩余定理合并

LUcas 定理

C(n, m) ≡ C(n / p, m / p) * C(n % p, m % p) (mod p) 
证明： 
核心思想：用两种方法展开 (x + 1) ^ n，考虑 x^m 一项的系数 
重要公式：(x + 1) ^ p ≡ x^p + 1 (mod p)

eg:

小 Q 的集合

给定 n, m, k，求 
∑(i <= n) C(n, i) * ( (i^k - (n-i)^k) ^ 2 ) mod m 
n <= 10^1000000 
m <= 1000000 
k <= 1000000

解： 
x ^ k ≡ (x % m) ^ k 
Lucas 定理、组合数公式

线性筛

一种优秀的筛法 
线性复杂度的来源：每个数只会被它的最小的质因子筛掉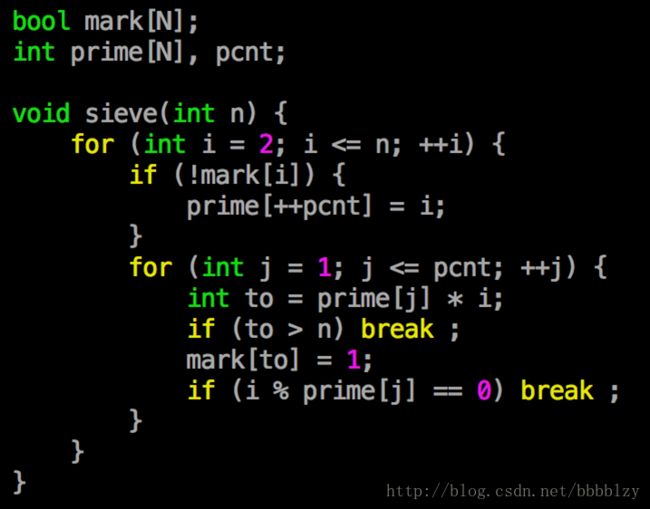 

简单证明： 设有一个数 m = p * q * s 
其中 p 是最小的质因子，q 是另外一个质因子 
如果 m 会被 q 筛掉，那一定是在 i = p * s 时筛掉的 
但是我们发现 i = p * s 时，j 枚举到 p 这个质数时就会 break 
把每个数被筛的过程画成一张图，发现相同的质因子是在连续的几步被筛掉的 
实际上，筛的过程相当于按照质因子降序分解了每个数

积性函数

若有函数 f(n) 的定义域为正整数，值域为复数，称为数论函数 
进一步地，若数论函数 f(n) 满足： 
对于互质的 p、q，有 f(p * q) = f(p) * f(q) 
称为积性函数，或者说函数满足积性 
更进一步地，若数论函数 f(n) 满足： 
对于任意 p、q，有 f(p * q) = f(p) * f(q) 
称为完全积性函数

常见的积性函数

除数函数 σk(n)=∑(d|n) d ^ k，表示n的约数的k次幂和 
约数个数函数 τ(n)=σ0(n)=∑(d|n) 1，表示n的约数个数，一般也写为d(n)。 
约数和函数 σ(n)=σ1(n)=∑(d|n) d，表示n的约数之和 
欧拉函数 ��(n) 
莫比乌斯函数μ(n)： 
n 有平方因子时值为 0 
否则值为 (-1) ^ (质因子个数) 
元函数 e(n) = [n = 1]，完全积性 
恒等函数 I(n) = 1，完全积性 
单位函数 id(n) = n，完全积性

Dirichlet卷积

对两个数论函数进行的运算 
设我们有两个数论函数 f(n) 和 g(n) 
它们的狄利克雷卷积是一个新的函数 (f * g) (n) 
设这个函数为 h 
我们有 h(n) = ∑(k|n) f(k) * g(n / k)

性质

积性函数的狄利克雷卷积仍然满足积性 
证明：对互质的 p、q，有 
h(p) * h(q) 
= ∑ { f(a) * g(b) | ab = p }* ∑ { f(c) * g(d) | cd = q } 
= ∑(ab = p, cd = q) f(ac) * g(bd) 
=∑(xy = pq) f(x) * g(y) 
=h(p * q) 
注意：完全积性函数的狄利克雷卷积不一定满足完全积性 
狄利克雷卷积满足结合律，即对于三个数论函数 f、g、h，有 (f * g) * h = f * (g * h) 
证明： 
(f * g) * h (n) 
= ∑(ab = n) h(b) * (∑(xy = a) f(x) * g(y)) 
= ∑(xyb = n) f(x) * g(y) * h(b) 
= ∑(xy = n) f(x) * (∑(ab = y) g(a) * h(b)) 
= f * (g * h) (n) 
Dirichlet 卷积同时也具有交换律、分配律 
Dirichlet 卷积运算存在单位元（元函数 e）：f * e = e * f = f

常见的公式

id = �� * 1 
d = 1 * 1 
σ = id * 1 
e = 1 * μ （反演式） ＊ 
�� = id * μ ＊

eg：····HDU 5628 
令 g(n) = ∑(i1|n) ∑(i2 | i1) ∑(i3 | i2) …∑(ik | ik - 1) f(ik) 
其中已经告诉你 f(i) 在 1 ~ n 的取值，没有特别规律 
求 g(1) ~ g(n) ，答案对 1e9 + 7 取模 
n、k <= 1e5

解： 
g = f * (1 ^ k) 
卷积满足结合律，1 ^ k可以用快速幂的思路乘 log n 次算出来 
如何求两个函数的狄利克雷卷积？ 
f(a) * g(b) => h(a * b) 
一次卷积德复杂度为 n * log(n) 
PS：本题存在一个 log 的组合解法

积性函数 的预处理

借助线性筛，可以在 O(n) 时间内预处理出某种数论函数在 [1, n] 的取值 
我们以约数个数函数为例说明 
莫比乌斯函数、欧拉函数、约数和函数的预处理都应该熟练掌握

约数个数函数

n = ∏ (pi^ai) 
d(n) = ∏ (ai + 1) 
我们维护一个辅助数组 num[x] ，表示 x 的最小的质因子的幂次 
线性筛每次会筛掉一个数最小的质因子，这让我们可以很方便地维护 num[]，从而计算 d[]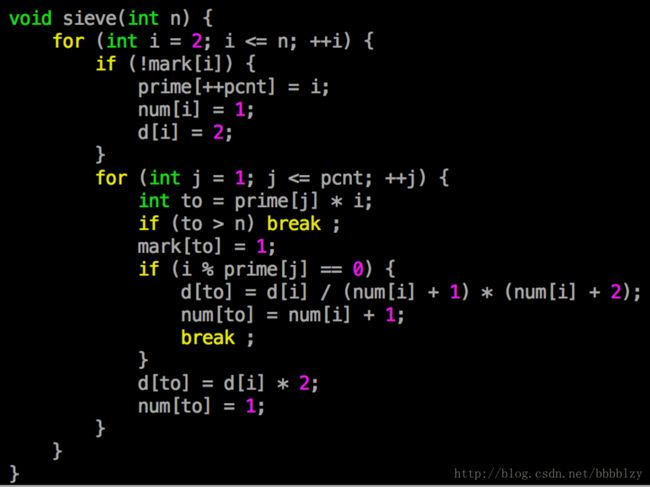 

离散对数

求解关于 x 的方程 A ^ x ≡ B (mod P) 
P 是质数，P <= 1e9

大步小步算法（bSGS）

我们设置一个步长 m 
则任意一个可行解可以写成 x = am + b (0 <= b < m) 
A ^ (am + b) = B mod P => A ^ b = B * A ^ (-am) mod P 
把 0 <= b < m 的 A ^ b 预先算出来，扔到哈希表中 
查询的时候暴力枚举 a，算出等式右边，在哈希表中查询 
复杂度 O(P / m) + O(m) 
m = √P 时，取得最优复杂度 O(√P) 
如果用 map 实现哈希表，还要乘一个 log

扩展大步小步法

如果 P 不是质数，怎么办？ 
若 (A, P) = 1，算法还是可以跑的，求逆元改成 extend_gcd 就行了 
(A, P) != 1时，问题出在哪儿？ 
A 不存在关于 P 的逆元 
令 d = gcd(A, P) 
A/d * A ^ (x - 1) = B/d (mod (P/d) ) 
递归求解 
最多 log(P) 层，注意最后算出来的答案 x 要加上层数 
因此，需要特判掉 x <= log(P) 的情况

ps：经过的今天的学习，告诉我们oier数学一定要学好 

第二天  搜索

搜索

搜索简介

搜索算法是利用计算机的高性能来有目的的穷举一个问题解空间的部分或所有的可能情况，从而求出问题的解的一种方法。 
现阶段一般有枚举算法、深度优先搜索、广度优先搜索、A* 算法、回溯算法、蒙特卡洛树搜索、散列函数等算法。 
在大规模实验环境中，通常通过在搜索前，根据条件降低搜索规模；根据问题的约束条件进行剪枝；利用搜索过程中的中间解，避免重复计算这几种方法进行优化。

平时大家写的暴力也在搜索的范畴之内

DFS/BFS

最基本的搜索框架 
各自有适用的场合

伪代码（吕欣大佬手打）：

void BFS(int s)
{
    queue Q;
    Q.push(s);
    vis[s]=true;
    while (!Q.empty())
    {
		int u=Q.front();
		Q.pop();
		// do sth
		for(int to:g[u])
		{
			if (!vis[to])
			{
				Q.push(to);
				//do sth
			}
		}
	}
}

eg:

文本编辑

有一个文本编辑器，它维护了一个字符串和一个光标 
字符串中只包含 a ~ g，且每个字符最多只出现一次 
光标在字符串开头/结尾/两字符之间 
允许的操作： 
将光标向前 / 后移动一个字符，消耗 1 点体力 
在光标前 / 后插入一个字符（需保证它没有出现过），消耗为 2 
删除光标前字符，消耗为 2 
给定初始字符串和光标位置，问将它转化为目标字符串最少多少步

解：用两个队列来维护BFS就可以啦！！！QAQ

NOIp 2015 斗地主

给定斗地主的一组手牌，问用合法规则将它们全部打完，最少需要多少轮 
多组询问 
N <= 23

解： 
考虑预处理 dp[x][y][z][w] 表示分别有 x、y、z、w 种出现 4、3、2、1 次的牌，不出顺子最少几步打完 
DFS 搜索打顺子的情况，结合 dp 计算答案 
最优性剪枝

Meet in middle

一种重要的优化搜索的手段 
如果搜索的问题能分成两部分，且两部分能够很高效的合并，那么可以使用中途相遇法来大大提高搜索的效率

方程的解数

已知 N 元高次方程： 
\sum_{i<=N} k[i] * x[i] ^ p[i] = 0 
设未知数均为不大于 M 的正整数，求解的个数 
N <= 6, M <= 150

解： 
将前半部分的搜索结果存入 Hash 表 
再搜后半部分

离散对数

给定素数 M 和整数 A、B 
解方程 A^x = B (mod M) 
给出任意一组解，或者说明无解 
A, B <= M <= 10^9

解: 
设步长 m 
那么任意一个解可以写成 x = km + r 
那么 A^{r} = A^{-km} * B (mod M) 
枚举可能的 r，把左半部分扔进 Hash 表 
枚举可能的 m，尝试寻找解 
复杂度 O(m) + O(M / m) >= O(\sqrt{M})

简单题

给定 4 个长度为 N 的整数数组，给定 M 
求：从 4 个数组中分别选一个数 a, b, c, d，使得 
abcd=1 (mod M) 
的方案数 
N <= 4000

启发式搜索

启发式搜索又称为有信息搜索，它是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的，这种利用启发信息的搜索过程称为启发式搜索。 
启发式搜索中应用最为广泛的搜索技巧当属 A* 和 IDA* 了 
前者是 BFS 的启法式版本，后者是前者的迭代加深版本

第三天  字符串&数据结构

字符串 Hash

···字符串 Hash:一种从字符串到整数的映射 
···通过这样的映射，把比较两字符串是否相同转化为两整数是否相同 
····若比较发现两字符串hash值相等，我们认为两字符串很大可能是相同的 
····另一方面，若 hash 值不等，则两字符串一定不同 
····比较字符串 O(L)，比较整数 O(1)

BKDR-Hash

··竞赛中常用的 hash 策略 
··把字符串视为一个 base 进制的大整数，对某个质数 P 取模得到 hash 值 
··sum_i = (sum_{i-1} *base + str_i) mod P 
··base 可以取 31、131、13131 等，需要满足 base > |字符集| 
··P 取 long long 范围内一个质数，注意溢出问题 
··使用 unsigned long long 自然溢出可以视为对 2^64 取模 
（电脑自动取最低的64位 即为自动取模） 
··但是可能被卡（对任意base） 
··害怕 Hash 被卡的同学，也可以选择双 hash（常数翻倍

常用技巧

····给定字符串 S，预处理出它的前缀 Hash 函数；同时计算好 mod P 意义下 base 的幂次表 
····sum[i] = (sum[i - 1] * base + str[i]) % P 
····pw[i] = (pw[i - 1] * base) % P 
····基础应用： 
··提取一段子串的 hash 值 
··合并两个串的 hash 值 
··O(\log n) 计算两个子串的 lcp 和字典序大小

想提取【l，r】的哈希值： 
【l，r】=s(r)-s(i-1)*10^(l+r-1)

eg: 
企鹅QQ 
给定 N 个长度均为 L 的串 
问有多少对字符串满足：恰好有一位对应不同 
N <= 30000, L <= 200

解：枚举删掉每一个位置，用 Hash 来进行答案统计

Trie 树 
又称字母树，可以用来维护字符串集合

优化思想是，利用字符串的公共前缀来减少查询时间，最大限度地减少无意义的比较

结构：有根树，每条边上存有一个字符 
从根到每个叶子的路径上经过的字符写下来，对应了一个字符串 
无敌伪代码： 

namespace Trie
{
	struct node
	{
		int ch[26];
		//other info
	}t[Max_M];
	int Root,pookCur;

	void inti()
	{
		Root=1;
		poolCur=2;
	}
	inline int newnode()
	{
		int o=poolCur++;
		memset(&t[o],0,sizeof(node));
		return poolCur++;

	}
	int insert(char s[],int n)//s[0..n-1]
	{
		int o=Root;
		for(int )
	}
}

支持的操作:插入、查找、删除

例 1

给定 2 * N 个字符串，你需要将它们配对起来 
两个字符串 x、y 配对的得分是它们的 lcp 长度 
最大化得分 
N <= 10^5，字符串总长 <= 2 * 10^6

解：建出 trie 树，两个串的 LCP 即为它们的 LCA 的深度 
使用贪心算法，按照树的 DFS 序列配对 
（树的DFS序列如图） 

例 2 
给定一棵有根树，每条边有权值 w_i 
求树上的一条简单路径，使得路径经过的边权异或和最大 
N <= 2 * 10^5, w_i <= 10^9

解： 
记录 dis[a] 表示 a 到根的链的异或和 
考虑 x、y 之间的链的异或和，设 LCA 为 z 
= (dis[x] ^ dis[z]) ^ (dis[y] ^ dis[z]) = dis[x] ^ dis[y] 
不难发现与 z 无关！ 
于是问题转化为，给定 N 个数，选出两个使得异或和最大

解 cont’d: 
考虑枚举两个数之一 x，我们想在其它数中找到一个与 x 的异或和最大 
从高到低考虑每一位，尽可能让更高位为 1 
不难发现可以使用 Trie 树！ 
复杂度 O(N * 32)

并查集

维护 N 个集合，初始时第 i 个集合为 { i } 
支持两个操作： 
把两个集合合并起来 
查询两个元素是否在同一集合 
N <= 10^6

原理:

对每个集合，建立一个有根树的结构 
令树的根为整个集合的“代表” 
想知道两个元素是否在同一集合，只需比较它们的代表 
合并时，将一棵树接到另一棵下边即可

优化策略

路径压缩 
按秩合并(把小的并到大的里面去) 
可以证明，使用这两种优化的并查集复杂度为 O(α(n)) 
绝大多数情况这个值不大于 5，可以认为是线性的

应用 
最小生成树的 Kruskal 算法 
Tarjan’s off-line LCA Algorithm

带权：

在一些应用中，可以在每个点上额外维护一些信息，表示“它与父亲”之间的关系 
进而尝试推算集合中任意两个元素之间的关系

例： 
某市有两个帮派，有 N 个人，每个人属于两个帮派之一。 
给定 M 个事件： 
1 x y，表示告诉你 x 和 y 属于同一帮派 
2 x y，表示告诉你 x 和 y 不属于同一帮派 
3 x y，表示请你推理 x 和 y 之间的关系 
N <= 5 * 10^5, M <= 10^6

解：

给每个人额外维护一个标记 rel[x] 表示 x 和 x 的父亲的关系 
由 rel[x] 和 rel[fa[x]] 可以推算 x 和 fa[fa[x]] 的关系。。。以此类推可以推算 x 和 Root[x] 的关系 
于是任意两个人只要在同一连通块，就能推算他们的关系 
问题：这个并查集如何使用路径压缩优化呢？

只按秩合并

只按秩合并的并查集，可以在合并的时候一定程度上保留元素合并在一起的 “过程” 
看一个经典例题

例

给定 N 个点，支持 M 个操作： 
1 x y，在 x 和 y 之间连边 
2 x y，询问 x 和 y 是否连通，如果是，那它们最早在哪一次操作之后连通的 
N <= 2 * 10^5, M <= 5 * 10^5

解：

@货车运输 
离线的时候可以建树倍增 blabla。。。 
强制在线呢？ 
只按秩合并，link(x, y, tim) 时，我们在 Root[x] 和 Root[y] 之间连一条边权为 tim 的边 
询问 (x, y) 时，找到 x 和 y 之间边权最大的边即可 
这种算法的复杂度是容易证明 O(\log N) 的正确性？

优先队列

支持这样几种操作的数据结构： 
插入一个优先级为 key 的元素 
询问优先级最高的元素 
删除优先级最高的 / 任意一个元素 
升高一个元素的优先级值

优先队列一般使用堆来实现

最经典的堆即为大名鼎鼎的二叉堆

二叉堆

二叉堆是一个完全二叉树结构，并且它具有堆性质： 
每个点的优先级高于它的两个孩子（如果有） 
可以用一个数字来存储二叉堆，避免指针： 
1 是根结点 
对于 x，它的左右孩子分别是 2x 和 2x+1 
容易验证 N 个点的二叉堆，它用到的数组即为 1 ~ N 
给定一个大小为 N 的数组，我们可以 O(N) 的建堆（How？

调整

随着操作的进行，二叉堆的“堆性质”可能会遭到破坏，为此我们定义两种调整操作，来维护二叉堆的堆性质保持不变

向上调整： 
当一个点的优先级升高时，我们需要向上调整 
比较它和它的父亲的优先级，它的优先级高就与父亲交换位置并递归进行 
向下调整： 
当一个点的优先级降低时，我们需要向下调整 
比较它和它左右儿子中优先级较高的那个，它的优先级低就与儿子交换并递归下去 
容易验证两种操作的复杂度均为 O(\log N)

操作

插入：插入一个叶子，然后向上调整 
询问：返回 a[1] 
删除根：令 a[1] = a[N]，然后向下调整

左偏树

也是一种优秀的堆 
并且是支持合并的（可并堆） 
比较简单，容易实现 
但是我们不讲

应用

Dijkstra 算法和 Prim 算法的优化 
哈夫曼编码 
一些奇怪的应用

例 1

给定数轴上 N 个点，你需要选出 2 * K 个，把它们配对起来 
把两个点配对起来的花费是它们坐标之差的绝对值 
最小化花费 
N <= 3 * 10^5

解： 
一定是取相邻两点配对 
问题可以转化为，选出 K 个相邻点对 
进一步转化为，有 N - 1 个线段，选出 K 个，且相邻的不同时选 
用堆进行贪心 
给贪心一个“修正”的余地： 
选了 p[i]，把 p[i - 1] + p[i + 1] - p[i] 入堆

例 2

炒股，一共有 2 * N 天，每天有一个买入和卖出价 
刚开始时你有 0 支股和充分多的钱 
每天要选择买或者卖一支股票（股票数时刻不为负 
最后一天结束你要清仓 
虽然你有充分多的钱，你还是想知道自己最多能在这些天赚到多少钱 
N <= 2 * 10^5

解：转化成括号序列问题？

线段树入门

线段树是一种二叉搜索树，一般可以用来维护序列的子区间

结构

对一个长度为 n 的序列建线段树，根结点即表示 [1, n] 
对于一个表示 [l, r] 的节点： 
若 l = r，则它是叶子 
否则，令 m = (l + r) / 2，它有左右两个孩子，分别记为：[l, m] 和 [m + 1, r] 
不难验证，这样一个线段树中有 2N - 1 个节点，并且树的深度是 O(\log N) 级别

原理

线段树的优化思想： 
根据问题的要求，用每个节点维护它对应的子区间中、可以高效合并的相关信息 
在动态的序列问题中，对于修改操作没有动过的部分。我们可以考虑把这些地方的求解的结果保存并复用，从而达到优化程序效率、降低复杂度的目的。

例 1

给定一个长度为 N 的序列，支持： 
修改一个位置的值 
查询一个子区间的元素和

解: 
线段树每个节点维护对应子区间的和 
区间覆盖： 
对于一个区间 [l, r]，我们可以将其分解为线段树上 O(\log N) 个节点的并； 
这里的分解是指，我们选取的区间并起来恰好为 [l, r]。且选择的区间不会相互重叠 
修改操作中，为了维护线段树性质，需要修改总共 O(\log N) 个节点 
查询操作，将区间拆为 O(\log N) 个区间的并，从而优化查询的复杂度 
总时间复杂度 O(\log N)

树状数组

一种支持单点修改和查询前缀和的数据结构 
复杂度为 O(\log N)，但是常数很小

原理

定义 lowbit(x)，表示将 x 写成二进制后，只保留二进制下最低一个 1 对应的整数 
例：lowbit(1001100) = 100, lowbit(1000) = 1000 
十进制：lowbit(76)=4, lowbit(8) = 8 
对一个数组 a[]，我们构造数组 c[]，其中 
c[i] = sum (. a[i - lowbit(i) + 1 … i] ) 
巧妙的事情来了： 
我们查询 a[] 的前缀和只需要访问 c 中 log N 个节点 
修改 a[] 中任意一个元素的值，只需要同时修改 c 中的 log N 个节点 
于是可以在 O(\log N) 的时间内支持单点修改、前缀和查询

树状数组 如图： 

Day4、5、6

动态规划（DP）

动态规划是noip最重要的知识点之一 刚开始学的时候理解起来有些困难 入门理解请见： 
转送们

线性DP复习

动态规划思想

三要素：阶段、状态、决策 
三前提：子问题重叠性、无后效性、最优子结构性质

动态规划是对问题空间进行的分阶段、有顺序、无重复、决策性的遍历求解类比有向无环图及其拓扑序

例题：

解析：

还有一些例题就不一一列举了 ，大家可以上各种oj上去切

背包问题

背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。（来自百度百科）

简单来说 背包就是DP中比较重要的一个分支

01背包

完全背包

eg： 

多重背包

直接拆分法

二进制拆分法

单调队列

eg：

分组背包

伪代码：

memset(f,0xcf,sizeof(f));
f[0]=0;
for(int I= 1;i<=n;++I)
    for(int j=m;j>=0;--j)
        for(int k=1;k<=c[i];++k)
         if(j>=v[I][k])
             f[j]=max(f[j],f[j-v[I][k]]+w[i][k]);

• 1
• 2
• 3
• 4
• 5
• 6
• 7

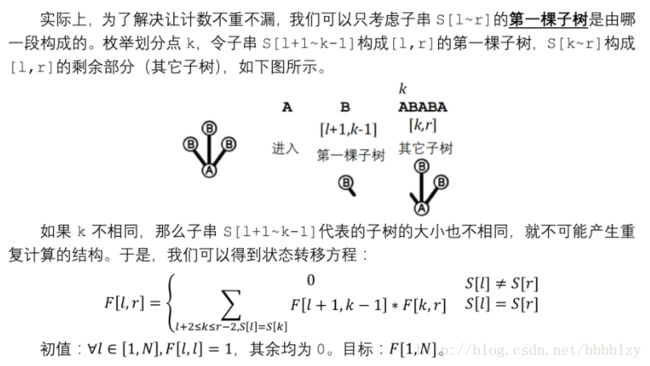
区间DP

经典例题：

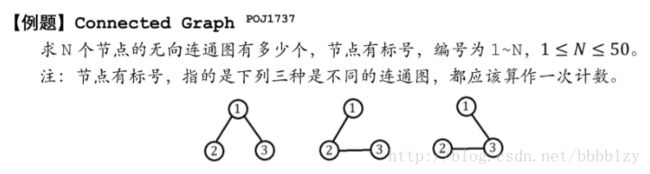
计数类DP

无向连通图计数

树形DP

背包类树形DP

伪代码（不保证能过）：

动态规划的优化

优化“阶段” ——倍增优化 
优化“状态” ——状态压缩动态规划 
优化“转移” ——矩阵乘法加速、数据结构优化、单调队列优化、斜率优化

伪代码： 

DP就像物理中的力学 又重要又难

老师讲DP的时候掉线频繁啊 
DP是个好东西 还得自己慢慢啃……