[数字图像处理]图像复原--逆滤波
1.逆滤波的问题点
图像的老化，可以视为以下这样的一个过程。一个是退化函数的影响（致使图片模糊，褪色等），一个可加性噪声的影响。
用算式表示为
前几篇博文，主要是介绍可加性噪声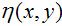
的去除。本博文，主要介绍图像的逆滤波，即退化函数
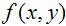的去除。然而，逆滤波在空间域内的处理是很不方便的。
的去除。本博文，主要介绍图像的逆滤波，即退化函数的去除。然而，逆滤波在空间域内的处理是很不方便的。
简单的来考虑，加法的逆运算是减法，乘法的逆运算的除法，微分的逆运算是积分(严密一点说是不定积分)。那么就可以得到一个简单的结论了，要出去卷积的话，肯定需要用到卷积的逆运算。卷积的逆运算是---------反卷积，额，好像是一个理所应当的名字。
我们建立了一个关于卷积的直观认识，将信号反转与滤波器系数求积和。那么，反卷积是一种什么样的运算呢？或者具体的来讲，反卷积的空间运算表现形式是什么样的？这样的考虑其实是多余的，或者说，不用考虑的那么复杂。
在之前的博文中([数字图像处理]频域滤波(1)--基础与低通滤波器)，我们得到这样的一个重要的结论。空间域内的卷积，其实就是频域内的乘积。那么这么考虑，就非常简单了，频域内的逆滤波运算，其实就是做除法。我们通过傅里叶变换，可以得到如下一个频域内的老化模型。
这样一个表达式内，没有了卷积运算，是一个很简单的四则运算。那么，所谓的去卷积或者逆滤波，就是将退化函数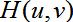
去除的过程。这样看来的话，直接做除法就可以了，如下所示。
去除的过程。这样看来的话，直接做除法就可以了，如下所示。
按照教材上的说法，这个表达式很有趣（哪里有趣了？）。首先，必须知道精确的退化函数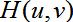。其次，如果退化函数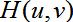含有0值或者极小值的话，会使得噪声项
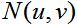变得极大。
。其次，如果退化函数含有0值或者极小值的话，会使得噪声项变得极大。
综上所述，其实逆滤波的问题点有两个：、
1.退化函数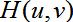的推测。
的推测。
2.尽可能的不让噪声项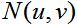影响画质。
影响画质。
2.两个退化函数的模型
2.1 大气湍流模型
这个模型很简单，与高斯LPF很相似。伴随着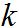
值的增大，得到的图像越来越模糊。以下是这个模型执行的结果。
值的增大，得到的图像越来越模糊。以下是这个模型执行的结果。
从表示式上可以看出，这个模型是不会有0值的，不过，这个模型与低通滤波器很相似，阻带的值都是极小的。这可能会使得图像的直接逆滤波失败。这个之后再说。
2.2 运动模糊模型
这个模型其实在Photoshop上也有一个同名的滤镜。详细的推倒我就不做了，这个模型的表达式如下所示。
这里有几个参数，说明一下。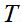
表示曝光时间，这里的
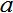与
表示了水平移动量与垂直移动量。值得一提的是，不要忘记下面这样一个重要的极限。
表示曝光时间，这里的与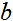表示了水平移动量与垂直移动量。值得一提的是，不要忘记下面这样一个重要的极限。
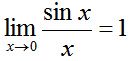
注意，运动模糊后的图像的尺寸会变化，如果还是按照原图截取，会造成图像成分的损失，在复原图像时候效果不是太好，而且不知道导致效果不好的原因，是由于成分的缺失，还是噪声的干扰。所以，这里我适当的扩展了图像的尺寸，以保留图像的所有成分
此模型的执行结果如下所示。
3.图像的逆滤波
3.1 实验步骤与实验用图像
我们是这样的一个实验步骤，首先，使用退化函数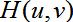处理图像，然后加上适当的可加性噪声。使用这样的图像进行逆滤波实验。
处理图像，然后加上适当的可加性噪声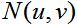。使用这样的图像进行逆滤波实验。
下面是实验用图像。图像的噪声选用的是高斯噪声，均值为0，方差为0.08。退化函数则选用先前叙述的两种，一个个大气湍流模型，一个是运动模糊。
3.2 直接逆滤波
所谓直接逆滤波，就是不管噪声的影响，直接进行逆滤波的方法。
对于大气湍流模型而言，直接逆滤波会得到很不理想的结果。下面是直接逆滤波的实验结果。
实验结果完全没有任何价值。观察其频谱，频谱的四角很亮，而原本频谱最亮的直流分量都看不到了。所以，这里做一个限制处理。也就是，仅仅只处理靠近直流分量的部分，其他的不做处理。然后处理完的结果，过一个10阶巴特沃斯低通滤波器。可以得到如下结果。
这样的话，只需要调整限制半径，可以得到一个比之前较好的结果。当然，这招在运动模糊的图片面前，就略显得无力了。结果我就不贴了。
3.3 维纳滤波器
维纳滤波器的推导，其实是个很复杂的过程。这里就不推导了，直接看结果，可以得到一些有用的结论。
观察式子，对于合适的常数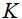
，有如下两个结论。
，有如下两个结论。
1.对于退化函数很小的点，相对而言常数
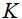的值很大，其倒数
不会太大。
的值很大，其倒数
不会太大。
2.对于退化函数很小的点，相对而言常数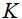的值很小，其倒数 基本保持不变。
的值很小，其倒数 基本保持不变。
下面的维纳滤波器的实验结果：
3.4 约束最小二乘方滤波
其实这个方法是一个很好的想法，将图像的能量作为评价图像平滑程度的度量，尽可能的将其平滑。设噪声的能量是一个定值，使用拉普拉斯未定系数法，将其进行迭代，然后解开。
这种方法有了很多的变种，包括很著名的TV(Total Variation，全变分)模型，这个我之后的博文会讲到。
在这里，使用本方法的目的是，减少噪音对于逆滤波的影响。表达式如下所示。
这个滤波器，可以消除很严重的噪声，并且复原图像。将实验用图像的噪声的方差提升到0.2，再进行滤波，可以得到如下结果。
4 实验代码
close all;
clear all;
clc;
%% ----------init-----------------------------
f = imread('./original_DIP.tif');
f = mat2gray(f,[0 255]);
f_original = f;
[M,N] = size(f);
P = 2*M;
Q = 2*N;
fc = zeros(M,N);
for x = 1:1:M
for y = 1:1:N
fc(x,y) = f(x,y) * (-1)^(x+y);
end
end
F_I = fft2(fc,P,Q);
figure();
subplot(1,2,1);
imshow(f,[0 1]);
xlabel('a).Original Image');
subplot(1,2,2);
imshow(log(1 + abs(F_I)),[ ]);
xlabel('b).Fourier spectrum of a).');
%% ------motion blur------------------
H = zeros(P,Q);
a = 0.02;
b = 0.02;
T = 1;
for x = (-P/2):1:(P/2)-1
for y = (-Q/2):1:(Q/2)-1
R = (x*a + y*b)*pi;
if(R == 0)
H(x+(P/2)+1,y+(Q/2)+1) = T;
else H(x+(P/2)+1,y+(Q/2)+1) = (T/R)*(sin(R))*exp(-1i*R);
end
end
end
%% ------the atmospheric turbulence modle------------------
H_1 = zeros(P,Q);
k = 0.0025;
for x = (-P/2):1:(P/2)-1
for y = (-Q/2):1:(Q/2)-1
D = (x^2 + y^2)^(5/6);
D_0 = 60;
H_1(x+(P/2)+1,y+(Q/2)+1) = exp(-k*D);
end
end
%% -----------noise------------------
a = 0;
b = 0.2;
n_gaussian = a + b .* randn(M,N);
Noise = fft2(n_gaussian,P,Q);
figure();
subplot(1,2,1);
imshow(n_gaussian,[-1 1]);
xlabel('a).Gaussian noise');
subplot(1,2,2);
imshow(log(1 + abs(Noise)),[ ]);
xlabel('b).Fourier spectrum of a).');
%%
G = H .* F_I + Noise;
% G = H_1 .* F_I + Noise;
gc = ifft2(G);
gc = gc(1:1:M+27,1:1:N+27);
for x = 1:1:(M+27)
for y = 1:1:(N+27)
g(x,y) = gc(x,y) .* (-1)^(x+y);
end
end
gc = gc(1:1:M,1:1:N);
for x = 1:1:(M)
for y = 1:1:(N)
g(x,y) = gc(x,y) .* (-1)^(x+y);
end
end
figure();
subplot(1,2,1);
imshow(f,[0 1]);
xlabel('a).Original Image');
subplot(1,2,2);
imshow(log(1 + abs(F_I)),[ ]);
xlabel('b).Fourier spectrum of a).');
figure();
subplot(1,2,1);
imshow(abs(H),[ ]);
xlabel('c).The motion modle H(u,v)(a=0.02,b=0.02,T=1)');
subplot(1,2,2);
n = 1:1:P;
plot(n,abs(H(400,:)));
axis([0 P 0 1]);grid;
xlabel('H(n,400)');
ylabel('|H(u,v)|');
figure();
subplot(1,2,1);
imshow(real(g),[0 1]);
xlabel('d).Result image');
subplot(1,2,2);
imshow(log(1 + abs(G)),[ ]);
xlabel('e).Fourier spectrum of d). ');
%% --------------inverse_filtering---------------------
%F = G ./ H;
%F = G ./ H_1;
for x = (-P/2):1:(P/2)-1
for y = (-Q/2):1:(Q/2)-1
D = (x^2 + y^2)^(0.5);
if(D < 258)
F(x+(P/2)+1,y+(Q/2)+1) = G(x+(P/2)+1,y+(Q/2)+1) ./ H_1(x+(P/2)+1,y+(Q/2)+1);
% no noise D < 188
% noise D < 56
else F(x+(P/2)+1,y+(Q/2)+1) = G(x+(P/2)+1,y+(Q/2)+1);
end
end
end
% Butterworth_Lowpass_Filters
H_B = zeros(P,Q);
D_0 = 70;
for x = (-P/2):1:(P/2)-1
for y = (-Q/2):1:(Q/2)-1
D = (x^2 + y^2)^(0.5);
%if(D < 200) H_B(x+(P/2)+1,y+(Q/2)+1) = 1/(1+(D/D_0)^100);end
H_B(x+(P/2)+1,y+(Q/2)+1) = 1/(1+(D/D_0)^20);
end
end
F = F .* H_B;
f = real(ifft2(F));
f = f(1:1:M,1:1:N);
for x = 1:1:(M)
for y = 1:1:(N)
f(x,y) = f(x,y) * (-1)^(x+y);
end
end
%% ------show Result------------------
figure();
subplot(1,2,1);
imshow(f,[0 1]);
xlabel('a).Result image');
subplot(1,2,2);
imshow(log(1 + abs(F)),[ ]);
xlabel('b).Fourier spectrum of a).');
figure();
n = 1:1:P;
plot(n,abs(F(400,:)),'r-',n,abs(F(400,:)),'b-');
axis([0 P 0 1000]);grid;
xlabel('Number of rows(400th column)');
ylabel('Fourier amplitude spectrum');
legend('F_{limit}(u,v)','F(u,v)');
figure();
n = 1:1:P;
plot(n,abs(H(400,:)),'g-');
axis([0 P 0 1]);grid;
xlabel('H''_{s}(n,400)');
ylabel('|H''_{s}(u,v)|');
%% ----------Wiener filters-----------
% K = 0.000014;
K = 0.02;
%H_Wiener = ((abs(H_1).^2)./((abs(H_1).^2)+K)).*(1./H_1);
H_Wiener = ((abs(H).^2)./((abs(H).^2)+K)).*(1./H);
F_Wiener = H_Wiener .* G;
f_Wiener = real(ifft2(F_Wiener));
f_Wiener = f_Wiener(1:1:M,1:1:N);
for x = 1:1:(M)
for y = 1:1:(N)
f_Wiener(x,y) = f_Wiener(x,y) * (-1)^(x+y);
end
end
[SSIM_Wiener mssim] = ssim_index(f_Wiener,f_original,[0.01 0.03],ones(8),1);
SSIM_Wiener
%% ------show Result------------------
figure();
subplot(1,2,1);
%imshow(f_Wiener(1:128,1:128),[0 1]);
imshow(f_Wiener,[0 1]);
xlabel('d).Result image by Wiener filter');
subplot(1,2,2);
imshow(log(1+abs(F_Wiener)),[ ]);
xlabel('c).Fourier spectrum of c).');
% subplot(1,2,2);
% %imshow(f(1:128,1:128),[0 1]);
% imshow(f,[0 1]);
% xlabel('e).Result image by inverse filter');
figure();
n = 1:1:P;
plot(n,abs(F(400,:)),'r-',n,abs(F_Wiener(400,:)),'b-');
axis([0 P 0 500]);grid;
xlabel('Number of rows(400th column)');
ylabel('Fourier amplitude spectrum');
legend('F(u,v)','F_{Wiener}(u,v)');
figure();
subplot(1,2,1);
imshow(log(1 + abs(H_Wiener)),[ ]);
xlabel('a).F_{Wiener}(u,v).');
subplot(1,2,2);
n = 1:1:P;
plot(n,abs(H_Wiener(400,:)));
axis([0 P 0 80]);grid;
xlabel('Number of rows(400th column)');
ylabel('Amplitude spectrum');
%% ------------Constrained_least_squares_filtering---------
p_laplacian = zeros(M,N);
Laplacian = [ 0 -1 0;
-1 4 -1;
0 -1 0];
p_laplacian(1:3,1:3) = Laplacian;
P = 2*M;
Q = 2*N;
for x = 1:1:M
for y = 1:1:N
p_laplacian(x,y) = p_laplacian(x,y) * (-1)^(x+y);
end
end
P_laplacian = fft2(p_laplacian,P,Q);
F_C = zeros(P,Q);
r = 0.2;
H_clsf = ((H')./((abs(H).^2)+r.*P_laplacian));
F_C = H_clsf .* G;
f_c = real(ifft2(F_C));
f_c = f_c(1:1:M,1:1:N);
for x = 1:1:(M)
for y = 1:1:(N)
f_c(x,y) = f_c(x,y) * (-1)^(x+y);
end
end
%%
figure();
subplot(1,2,1);
imshow(f_c,[0 1]);
xlabel('e).Result image by constrained least squares filter (r = 0.2)');
subplot(1,2,2);
imshow(log(1 + abs(F_C)),[ ]);
xlabel('f).Fourier spectrum of c).');
[SSIM_CLSF mssim] = ssim_index(f_c,f_original,[0.01 0.03],ones(8),1);
figure();
subplot(1,2,1);
imshow(log(1 + abs(H_clsf)),[ ]);
xlabel('a).F_{clsf}(u,v).');
subplot(1,2,2);
n = 1:1:P;
plot(n,abs(H_clsf(400,:)));
axis([0 P 0 80]);grid;
xlabel('Number of rows(400th column)');
ylabel('Amplitude spectrum');
原文发于博客：http://blog.csdn.net/thnh169/
=============更新日志===================
NULL