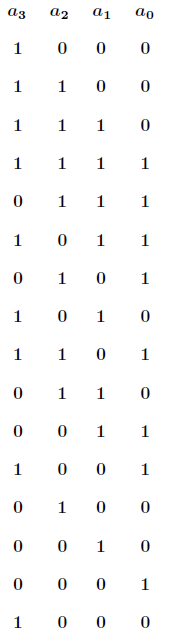伪随机数生成算法-梅森旋转(Mersenne Twister/MT)算法介绍
今天主要是来研究梅森旋转算法,它是用来产生伪随机数的,实际上产生伪随机数的方法有很多种,比如线性同余法,
平方取中法等等。但是这些方法产生的随机数质量往往不是很高,而今天介绍的梅森旋转算法可以产生高质量的伪随
机数,并且效率高效,弥补了传统伪随机数生成器的不足。梅森旋转算法的最长周期取自一个梅森素数![]() ,
,
由此命名为梅森旋转算法。常见的两种为基于32位的MT19937-32和基于64位的MT19937-64。
由于梅森旋转算法是利用线性反馈移位寄存器(LFSR)产生随机数的,所以我们先来认识线性反馈移位寄存器。
首先,移位寄存器包括两个部分
(1)级,每一级包含一个比特,比如11010110是一个8级的移位寄存器产生的
(2)反馈函数,线性反馈移位寄存器的反馈函数是线性的,非线性反馈移位寄存器的反馈函数是非线性的
一个![]() 级的移位寄存器产生的序列的最大周期为
级的移位寄存器产生的序列的最大周期为![]() ,当然这个最大周期跟反馈函数有很大关系,线性反馈函数实
,当然这个最大周期跟反馈函数有很大关系,线性反馈函数实
际上就是这个![]() 级的移位寄存器选取“某些位”进行异或后得到的结果,这里的“某些位”的选取很重要,得到线性反馈
级的移位寄存器选取“某些位”进行异或后得到的结果,这里的“某些位”的选取很重要,得到线性反馈
函数之后,把这个移位寄存器的每次向右移动一位,把最右端的作为输出,把“某些位”的异或结果作为输入放到最左
端的那位,这样所有的输出对应一个序列,这个序列叫做M序列,是最长线性移位寄存器序列的简称。
上面“某些位”的选取问题还没有解决,那么应该选取哪些位来进行异或才能保证最长周期为![]() ,这是一个很重要
,这是一个很重要
的问题。选取的“某些位”构成的序列叫做抽头序列,理论表明,要使LFSR得到最长的周期,这个抽头序列构成的多项
式加1必须是一个本原多项式,也就是说这个多项式不可约,比如![]() 。
。
下面以一个4位的线性反馈移位寄存器为例说明它的工作原理。
![]()
如果![]() 的值分别是1 0 0 0,反馈函数选取
的值分别是1 0 0 0,反馈函数选取![]() ,那么得到如下序列
,那么得到如下序列
可以看出周长为15。在这一个周期里面涵盖了开区间![]() 内的所有整数,并且都是没有固定顺序出现的,有
内的所有整数,并且都是没有固定顺序出现的,有
很好的随机性。
之前说过,梅森旋转算法的周期为![]() ,那么说明它是一个19937级的线性反馈移位寄存器,实际上基于32位
,那么说明它是一个19937级的线性反馈移位寄存器,实际上基于32位
的MT19937-32只需要用到32位,那么为什么要选择周长为![]() 的算法呢? 那是因为这样做随机性很好。
的算法呢? 那是因为这样做随机性很好。
梅森旋转算法是基于线性反馈移位寄存器的一直进行移位旋转,周期为一个梅森素数![]() ,果然是名副其实。
,果然是名副其实。
梅森旋转算法(Mersenne twister)是一个伪随机数发生算法。由松本真和西村拓士[1]在1997年开发,基于有限二进制字段上的矩阵线性递归![]() 。可以快速产生高质量的伪随机数, 修正了古典随机数发生算法的很多缺陷。
。可以快速产生高质量的伪随机数, 修正了古典随机数发生算法的很多缺陷。
梅森旋转算法是R,Python,Ruby,IDL,Free Pascal,PHP,Maple,Matlab,GMP和GSL的默认伪随机数产生器。从C++11开始,C++也可以使用这种算法。在Boost C++,Glib和NAG数值库中,作为插件提供。 在SPSS中,梅森选旋转算法是两个PRNG中的一个:另一个是产生器仅仅为保证旧程序的兼容性,梅森旋转被描述为”更加可靠“。梅森旋转在SAS中同样是PRNG中的一个,另一个产生器是旧时的且已经被弃用。
最为广泛使用Mersenne Twister的一种变体是MT19937,可以产生32位整数序列。具有以下的优点:
- 有219937 − 1的非常长的周期。在许多软件包中的短周期—232 随机数产生器在一个长周期中不能保证生成随机数的质量。[2
- 在1 ≤ k ≤ 623的维度之间都可以均等分布(参见定义).
- 除了在统计学意义上的不正确的随机数生成器以外, 在所有伪随机数生成器法中是最快的(当时)
算法详细
本算法基于标准(线性)旋转反馈移位寄存器(twisted generalised feedback shift register/TGFSR)产生随机数
算法中用到的变量如下所示:
·w:长度(以bit为单位)
·n:递归长度
·m:周期参数,用作第三阶段的偏移量
·r:低位掩码/低位要提取的位数
·a:旋转矩阵的参数
·f:初始化梅森旋转链所需参数
·b,c:TGFSR的掩码
·s,t:TGFSR的位移量
·u,d,l:额外梅森旋转所需的掩码和位移量
MT19937-32的参数列表如下:
·(w, n, m, r) = (32, 624, 397, 31)
·a = 9908B0DF(16)
·f = 1812433253
·(u, d) = (11, FFFFFFFF16)
·(s, b) = (7, 9D2C568016)
·(t, c) = (15, EFC6000016)
·l = 18
MT19937-64的参数列表如下:
·(w, n, m, r) = (64, 312, 156, 31)
·a = B5026F5AA96619E9(16)
·f = 6364136223846793005
·(u, d) = (29, 555555555555555516)
·(s, b) = (17, 71D67FFFEDA6000016)
·(t, c) = (37, FFF7EEE00000000016)
·l = 43参考链接:
https://github.com/xuwei-k/tinymt
https://en.wikipedia.org/wiki/Mersenne_Twister#TinyMT
http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/TINYMT/JAVA/index.html
https://cs.gmu.edu/~sean/research/mersenne/MersenneTwister.java
https://cs.gmu.edu/~sean/research/mersenne/MersenneTwisterFast.java